Добавил:

quantum researchgate.net Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесский государственный экологический университет

Предмет:

Алгебра и начала анализа

Файл:

978-966-10-2413-6_Matematuka 11_rus

.pdf

Скачиваний:

Добавлен:

24.03.2018

Размер:

10.66 Mб

Скачать

☆

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 2324 / 4824 25 26 27 28 29 30 31 32 33 34 35 36 > Следующая >>>

Интеграл

231

2.Точка, двигаясь прямолинейно со скоростью v = t3, за неко- торый промежуток времени преодолела

путь S. Какой путь она пройдет за тот же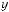

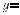
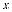
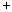
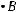
промежуток времени, если ее скорость бу- дет изменяться по закону v =(2t)3?

Площадь криволинейной трапеции aABb, изображенной на рис. 149, равна S. Чему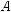

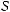
равна площадь криволинейной трапеции

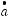
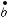
?1 1

	1	2
4.	Чемуравен ò f (x)dx ,если ò f (x)dx = 2,7игра
	0	0
	фик функции y = f (x) изображен на рис. 150?

Задачи

195. Вычислите интеграл:

1°)

∫ dx ;

2°) ò dx

;

3°) ò dx2 ;

−1

4°)

xdx ;

5°)

∫

;

∫ e2x dx ;

sin

−1

x −1

ò x

xdx ;

8) ∫

−

x dx ; 9)

∫ 2

dx .

x +1

−1

196°. Найдите площадь криволинейной трапеции, ограниченной

линиями:

1) y =

1 , x =

1, x = e, y = 0 ;

y = 2x , y = 0, x = −1, x = 1 ;

y = x2 , x = −1, x = 2, y = 0;

y = sin x, y = 0, x = 0, x = π.

197°. Изобразите криволинейную трапецию, площадь которой
равна:								π
	2			3				2
1)	∫ x2dx ;	2)		∫	xdx	;	3)	∫cos xdx;
	−1			0				0
	2		2					π
	2		2					3
4)	∫ex dx;	5)	∫ln xdx;				6)	∫tg x dx.
	0		1					π
								4

232

Раздел 4. Интеграл и его приложения

198°. Точка совершает гармонические колебания со скоростью

v = sint

, где v — скорость, м/с; t

— время, с. Найдите путь,

пройденный точкой за промежуток времени [0;

π].

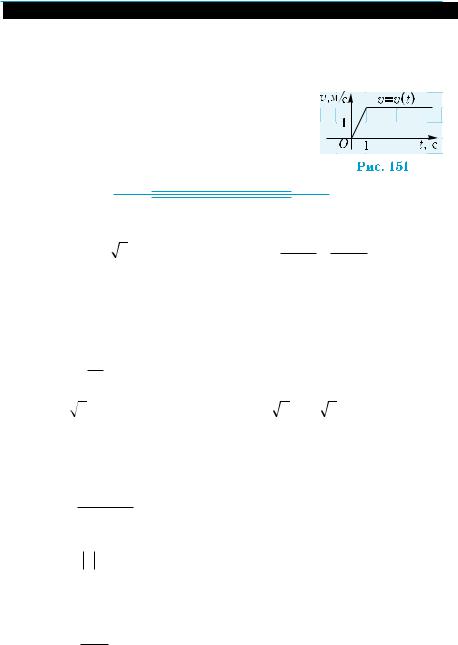
199°. Точка движется прямолинейно со скоростью v = v(t), график

которой изображен на рис. 151.

1) Определите, какой путь она пройдет за

промежуток времени [0; 2]; [0,5; 1]; [1; 2].

2) Выразите путь, пройденный точкой за

промежуток времени [0,5; 1], с помощью

интеграла.

200.

Вычислите интеграл:

1°)

− 2 x )dx ;

2°)

∫

sin

dx ;

cos

cos x

3°)

4°)

+ 3

−1)dx ;

∫

4x dx ;

∫

−

−1

5°)

∫ x

6°)

∫ (2x −1)(2x +1)dx ;

dx ;

−1

x +1)2 dx ;

∫(

∫

(

x +1)(

x −1)dx;

−1

(1 + x + x2 )dx;

10)

dt ;

∫

∫ (t + 2)

−2 x

4dx

1 6x + 6

11)

;

12*)

dx ;

∫

−

π 1 − sin

−1

13*)

∫ x (x − 2)dx ;

−3

1 x ≤ 0,

14*)

∫ f (x)dx , если f (x)

x >

−2

15*)

;

16*)

−

∫

∫sin

dx .

Интеграл

233

201.Скорость точки изменяется по закону v = 4t – t2, где v — ско- рость, м/с; t — время, с. Найдите путь, пройденный точкой: 1°) за первые 2 с движения; 2°) за третью секунду движения;

3)от начала движения до момента, когда она изменит на- правление движения.

202.Найдите путь, пройденный автобусом за время от начала торможения (t = 0) до полной его остановки, если при тор- можении скорость этого автобуса изменялась по закону

20 – 4t, где v — скорость, м/с; t — время, с.

Два объекта начали движение по прямой одновременно из одной точки в одном направлении. Их скорости изменялись

по законам: v = 2cos t и v = 12π2t , где v — скорость, м/с; t — вре-

мя, с.

1°) Какой из объектов прошел больший путь за промежуток

времени		π	?
времени	0;		?
		6
2) Какое расстояние было между объектами в тот момент,

когда первый из них впервые изменил направление движе- ния?

Упражнения для повторения

204. Найдите координаты точек пересечения графиков функций:
1°) у = х2 – х – 1 и	у = 1;	2°) у = \|2x – 3\| и у =	3;
3) у = х2 и y = x ;		4) у = 2х и у = х + 1.

205.Изобразите фигуры, ограниченные графиками функций, приведенных в упражнении 204.

234	Раздел 4. Интеграл и его приложения

Итог

Основные понятия

Определение Геометрическая интерпретация

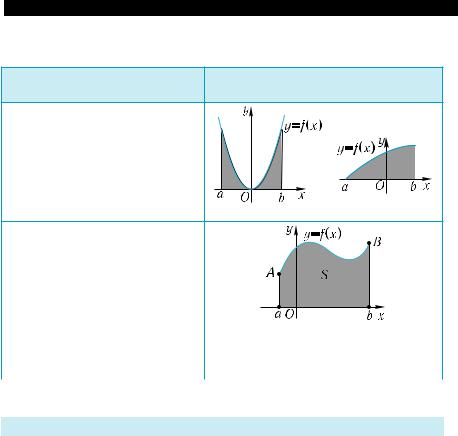
Фигура, ограниченная гра- фиком непрерывной неотри- цательной функции y = f(x), отрезком [a;b] оси х и отрез-

ками прямых х = а, х =b ,

называется криволинейной

трапецией .

Приращение первообразной для непрерывной функции y = f (x) на промежутке [a;b]

называется интегралом от функции y = f (x) на

промежутке [a; b]:

b
∫ f(x)dx = F(b) − F(a).				b
a				S = ∫ f(x)dx.
				a

		Основные утверждения

Словесная формулировка			Символическая запись
Интеграл от суммы функ-			b	b	b
ций равен сумме интегралов			∫( f (x) + g(x))dx = ∫ f (x)dx +∫ g(x)dx
от этих функций.			a	a	a
Постоянный	множитель		b	b
можно выносить за знак ин-			∫ kf (x)dx = k∫ f (x)dx
теграла.			a	a
Если промежуток		интегри-
рования разбить на два не-
пересекающихся		промеж-	b	c	b
утка, то интеграл по всему			∫ f (x)dx = ∫ f (x)dx +		∫ f (x)dx
промежутку	равен сумме		a	a	c
интегралов по промежуткам
разбиения.

§11. Применение интеграла

В данном параграфе находятся с помощью интеграла площади фигур, более сложных по сравнению с криволинейной трапецией, а также рассматриваются основные схемы применения интеграла для решения прикладных задач.

Вычисление площадей плоских фигур

соответствии с геометрической интерпретацией ин- теграла (§10) площадь S криволинейной трапеции, ограниченной графиком непрерывной неотрицатель- y = f (x) , прямыми х = а, х = b и осью абсцисс, равна:

S = ∫ f(x)dx . (1)

Однако с помощью интеграла можно вычислять площади не только криволинейных трапеций, но и более сложных фигур.

В этих случаях используют следующие свойства площадей:

1)если фигуру разбить на конечное число фигур, не име- ющих общих внутренних точек, то ее площадь равна сумме площадей этих фигур;

2)площадь фигуры сохраняется при перемещении, в частности при параллельном переносе и преобразовании симметрии относительно точки и прямой.

Вычислим, например, площадь фигуры аАВb (рис. 152, а), ог- раниченной графиком непрерывной, неположительной функции y = f (x) и прямыми x = a , x = b, y = 0 . Эта фигура симметрична

относительно оси х криволинейной трапеции aA1B1b , ограничен- ной линиями y = −f (x) , x = a , x = b, y = 0 (рис. 152, б). Следова- тельно, площадь аАВb равна площади aA1B1b , то есть

b	b
S = ∫(−f(x))dx = −∫ f(x)dx .		(2)

236					Раздел 4. Интеграл и его приложения

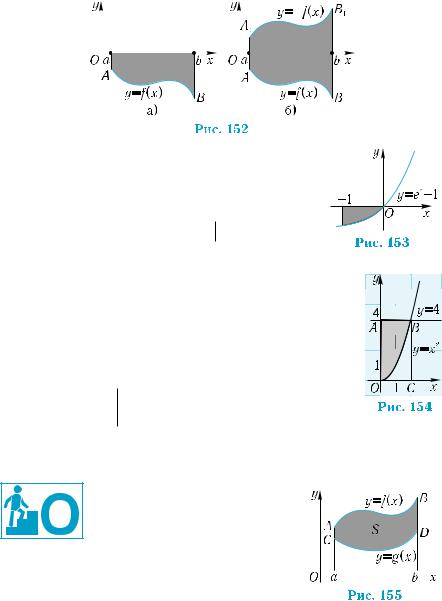
Пример 1. Вычислить площадь фигуры,
ограниченной линиями у = ех – 1,							у = 0, x = −1
(рис. 153).
Согласно формуле (2), имеем:
	0	(ex − 1)dx = (−ex + x) 0−1 = e−1 . g
S = − ∫
Ответ.	−1
	е–1.
Пример	2.	Вычислить площадь фигуры, ограни-
ченной линиями у = х2, y = 4, x = 0							(рис. 154).
Фигура ОАВ не является криволинейной трапе-
цией, но дополняет криволинейную трапецию ОВС
до прямоугольника					ОАВС. Поэтому искомая пло-
щадь S равна:			S = SOABC			– SOBC. Так как		SOABC = 8,
2		= x	3	2	8 , то	S = 8 − 8	= 16 = 5	1 . g
SOBC = ∫ x2dx				=
0		3		0	3	3	3	3
Ответ. 51 .
	3

Рассмотрим фигуру, ограни-

ченную прямыми х = а, х = b и графиками непрерывных фун-

кций y = f (x), y = g(x) таких, что f (x) ≥ g(x) ≥ 0 на отрезке [a;b] (рис. 155).

Криволинейная трапеция аСDb дополня- ет данную фигуру САВD до криволинейной

трапеции аАВb. Поэтому, обозначив площади

этих фигур соответственно через S1 , S, S2 , получим: S2 = S + S1 ,

Применение интеграла										237
или S = S2 − S1	. Таким образом, площадь фигуры САВD можно
вычислять по формуле
				b
		S = ∫( f(x) − g(x))dx .								(3)
Пример 3.	Вычислите aплощадь фигуры, огра-
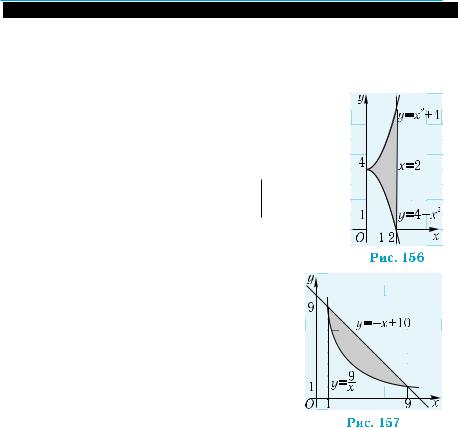
ниченной линиями у = х2 + 4,						y = 4 − x2 ,				x = 2
(рис. 156).
Согласно формуле (3), имеем:								2
2				2		2x	3	2	1	. g
S = ∫(x2 + 4 + x2 − 4)dx = 2∫x2dx =						2x		= 5	1	. g
0				0		3		0	3
Ответ. 51 .
3	Вычислите площадь фигуры,
Пример 4.	Вычислите площадь фигуры,
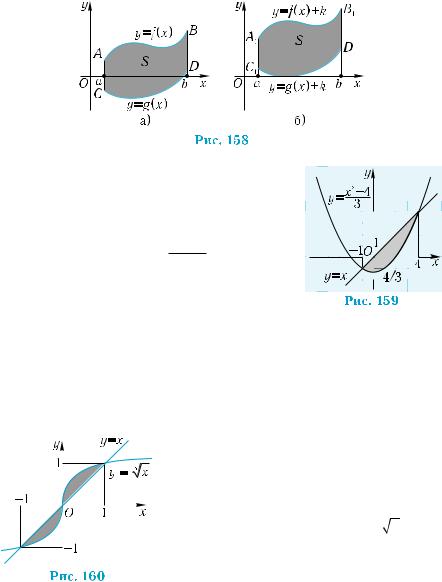
ограниченной	линиями			y = −x +10 ,				y = 9
(рис. 157).								x
(рис. 157).
 Чтобы найти абсциссы точек пересе-
чения линий	y = −x + 10 и				y = 9	, решим
	9 = −x +10;				x
уравнение	9 = −x +10;				9 = −x2 +10x,
	x			= 9 .
x2 −10x + 9 = 0, x =1, x			2	= 9 .
	1		2
Воспользовавшись формулой (3), получим:

S =

−x +10

−

∫1

dx =

+10x − 9ln x

= 40 − 9ln 9 ≈ 20,2 .

Ответ. ≈ 20,2.

Формулу (3) можно применять и для вычисления площадей фи- гур вида АСDВ (рис. 158, a), то есть фигур, ограниченных прямыми х = а, x = b и графиками непрерывных на отрезке [a;b] функций

y = f (x), y = g(x) , удовлетворяющих неравенству g(x) £ f (x) .

Действительно, перенесем фигуру АСDВ параллельно вдоль оси у на некоторое расстояние k так, чтобы она оказалась выше оси х (рис. 158, б). Фигура A1C1D1B1 получена из фигурыАСDВ путем па-

раллельного переноса, а потому они имеют равные площадиS. Для вычисления площади A1C1D1B1 применяем формулу (3), то есть

238		Раздел 4. Интеграл и его приложения

	b	b
	S = ∫( f(x) + k − g(x) − k)dx = ∫( f(x) − g(x))dx .
	a	a

Пример 5.	Вычислить площадь фигуры,
ограниченной линиями		y =	1	(x2		− 4) ,	y = x
(рис. 159).			3
(рис. 159).
 Решая	уравнение	x2	− 4		= x , найдем
 Решая	уравнение	3			= x , найдем
		3
абсциссы точек пересечения графиков фун-
кций y = 1 (x2 − 4) и y = x			:	x		= −1, x	2	= 4 .
3				1			2
Согласно формуле (3), имеем:

		4			2
	S = ∫		x − x
		−1		3
Ответ. 6		17 .
		18

+	4			2	− x	3	+	4x	4	= 6	17	. g

		dx = x
	3		2		9			3	−1		18

При вычислении площадей целесо образно учитывать симметрию фигуры от- носительно осей и начала координат. Это существенно сокращает вычисления. На- пример, при вычислении площади фигу-

ры, ограниченной линиями y = 3 x , y = x

(рис. 160), достаточно вычислить площадь только одной ее половины и результат уд- воить.

Применение интеграла

239


	99
	99	Контрольные вопросы
1°.		Какими свойствами обладает площадь фигуры?
		1
2°.		Верно ли, что интеграл ∫ x3dx равен площади фигуры, огра-
		−1
		ниченной линиями x = −1, x = 1,	y = 0, y = x3 ?
				a
3.		Функция y = f (x) является четной (нечетной) и		∫ f (x)dx = 1 .
		0	a	0
		0	a
		Чему равен интеграл: а) ∫ f (x)dx;	б) ∫ f (x)dx ?

−a −a

4.Известно, что площадь криволинейной трапеции, ограничен- ной прямыми х = 0, х = 2, графиком функции у = f(x) и осью х, равна 1. Чему равна площадь фигуры, ограниченной:

а) прямыми х = 0, х = 2, графиком функции у = –f(x) и осью х; б) прямыми х = 0, х = 2, графиком функции у = f(x)+ 1 и осью х; в) прямыми х = 1, х = 3, графиком функции у = f(x – 1) и осью х?

5.Выразите интеграл ∫b f(x)dx через площади фигур S1, S2, S3, изображенных на: а)aрис. 161; б) рис 162.

6.Как целесообразно вычислить площадь фигуры, изображен-

ной на: рис. 163, а); рис. 163, б); рис. 163, в); рис. 163, г)?

240 Раздел 4. Интеграл и его приложения

7. На рис. 164 изображены графики фун-
7. На рис. 164 изображены графики фун-
	кций	у = f(x), у = g(x). Используя геоме-
	трический смысл				интеграла,	сравните
			b		b
	числа:		ò f (x)dx и		ò g(x)dx.


			a		a
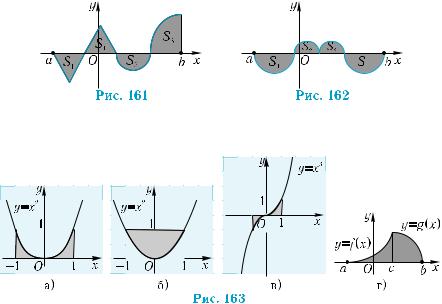
8*. Чему равен интеграл:						1
2		x				1
	а) ∫	x		dx ;	б)	∫ 1 − x2 dx ?
	а) ∫	2		dx ;	б)	∫ 1 − x2 dx ?
	−2 x	+ 1				−1

2. Применение интеграла в физике

Существуют две основные схемы применения ин- теграла. Первая схема основывается на формуле

∫ F ′(x)dx = F(b) − F(a) .

Если известна скорость F ′(x) протекания некоторого процесса (то есть скорость изменения величины F(x) со временем), то с по- мощью этой формулы можно определить, на сколько изменится исследуемая величина за промежуток времени [а; b]. Формула


T	T
∫v(t)dt = ∫ x (t)dt = x(T ) − x(t0 ) , с помощью которой мы находили
	′
t0	t0
перемещение прямолинейно движущейся точки, является част-
ным случаем формулы, приведенной выше.
Пример 6. Шкив вращается с угловой скоростью ω =		t +1	, где

	2
w — угловая скорость, рад/с; t — время, с. На какой угол повернет-
ся шкив за третью секунду вращения?
	 Пусть j = j (t) — угол поворота шкива за промежуток време-
ни [0; t]. Тогда j ′(t) = w (t) — его угловая скорость вращения. Зна-

чит, угол поворота шкива за промежуток времени [2;3] равен:

ϕ(3) − ϕ(2)	3	′	3	3 t +		1	dt =	7	(рад). g
ϕ(3) − ϕ(2)	= ∫ϕ (t)dt = ∫ω(t)dt = ∫				2		dt =	4	(рад). g
	2		2	2	2			4
Ответ.	7	рад.
	4		Скорость изменения концентрации вещества,
Пример	7.		Скорость изменения концентрации вещества,
вступившего в реакцию, выражается формулой v = 3t + 1										, где v —

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 2324 / 4824 25 26 27 28 29 30 31 32 33 34 35 36 > Следующая >>>