
978-966-10-2413-6_Matematuka 11_rus
.pdf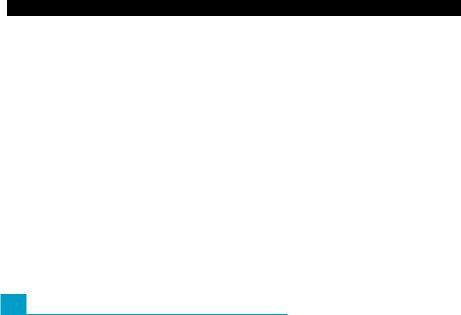
Пирамиды и конусы |
281 |
3)образующую прямого кругового конуса, высота которого совпадает с высотой пирамиды, а радиус основания — с ка- тетом основания пирамиды;
4)площадь сечения этого конуса плоскостью, проходящей через его вершину и середины катета и гипотенузы тре угольника, лежащего в основании пирамиды.
233.Отношение площади основания прямого кругового конуса к площади осевого сечения равно p. Определите угол наклона образующей к основанию.
234.Высота прямого кругового конуса равна H. На каком рассто- янии от вершины следует провести плоскость, параллель- ную основанию, чтобы площадь сечения равнялась полови- не площади основания?
235.Две плоскости, параллельные основанию, делят высоту ко- нуса на три равные части. Сравните сумму площадей сече- ний с площадью основания конуса.
Упражнения для повторения
236.Докажите, что при параллельном переносе плоскость ото- бражается на плоскость, параллельную данной или совпа- дающую с ней.
237.Опишите сечения прямоугольного параллелепипеда пло- скостями, параллельными граням и ребрам.
238.Прямоугольную подставку, расположенную горизонталь- но, заполнили карандашами, поставленными вертикально, одинаковой длины. Какую форму имеет полученная кон- струкция? А если подставка круглая?
282 |
Раздел 5. Геометрические тела и поверхности |
Итог
Конусом нaзывaетcя гeoмempuческая фигура, обра- зованная отpезкaмu, соединяющими все moчкu дан- ной nлocкoй фигуры с moчкoй, расположенной вне
nлoскости фигуры.
Пирамида является конусом, основанием которого является мнoгoугольник.
Основные утверждения
1.В правильной пирамиде боковые ребра равны между собой и одинаково наклонены к плоскости основания, а боковые грани — равные между собой равнобедренные треугольники, одинаково наклоненные к плоскости основания.
2.Сечение конуса плоскостью, параллельной плоскости его осно- вания, подобно основанию конуса, и коэффициент подобия равен отношению расстояния между вершиной конуса и пло- скостью сечения к высоте конуса.
§13. Призмы и цилиндры
Данный параграф посвящен рассмотрению двух классов фигур — призм и цилиндров, отдельные представители которых вам хорошо известны. Исследование строения и свойств призм и цилиндров является главной его целью. Эти фигуры строятся также из отрезков, но иным способом по сравнению с пирамидами и конусами.
1. Призмы
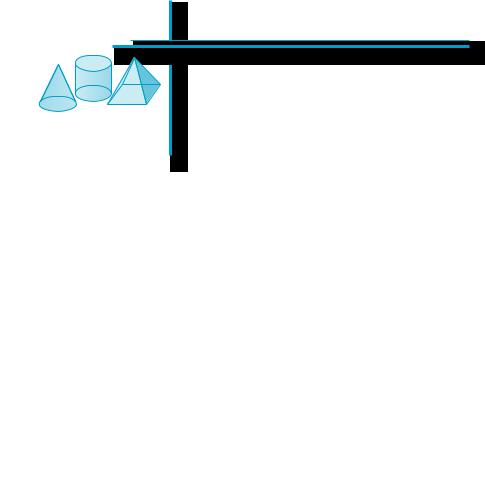
течение всей жизни мы постоянно имеем дело с предметами, части которых или сами они имеют форму параллелепипеда (рис. 215, а–в).
Параллелепипед можно сконструировать из равных и парал- лельных между собой отрезков, проведенных из всех точек парал- лелограмма по одну сторону от его плоскости (рис. 216).
По аналогии с пирамидами обобщение этого построения приво- дит нас к понятию призмы.
Пусть дан произвольный многоугольник (рис. 217, а). Отложим из каждой его точки равные и параллельные между собой отрезки по одну сторону от плоскости многоугольника (рис. 217, б). Фигу- ра, составленная из всех точек построенных отрезков, называет- ся призмой. Отрезки, отложенные при ее построении, называют
образующими призмы.
284 |
Раздел 5. Геометрические тела и поверхности |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Призма — от греческого πρισµα (prisma), от πριω (prio) — пилю, буквально: отпиленный кусок.
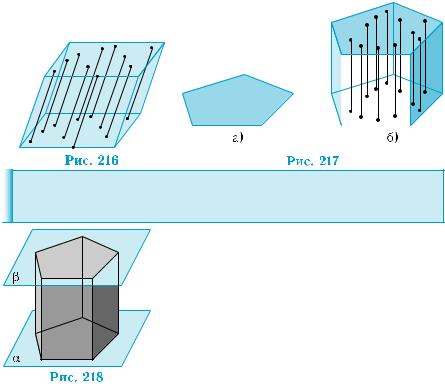
Концы образующих призмы лежат в па- раллельных плоскостях и образуют два рав- ных многоугольника (рис. 218). Это следует из того, что построенные отрезки определя- ют параллельный перенос данного многоу- гольника на вектор, модуль которого равен длине построенных отрезков, а направле- ние совпадает с направлением этих отрез- ков, если точку, от которой откладывается
отрезок, считать его началом.
По свойству параллельного переноса плоскость a, в которой ле- жит данный многоугольник, отображается на параллельную ей плоскость b, в которой содержатся концы построенных отрезков. При этом данный многоугольник в плоскости a отображается на равный ему многоугольник в плоскости b. Эти многоугольники называются основаниями призмы. Расстояние между плоско- стями оснований называется высотой призмы.
В зависимости от вида многоугольника, лежащего в основании (треугольник, четырехугольник, ..., n-угольник), призмы называ-
ются треугольными, четырехугольными, ..., n-угольными.
Поверхность призмы состоит из многоугольников, которые называются гpaнямu, их стороны — pебpaмu, а вершины — вepшuнaмu npuзмы. Две грани призмы — это параллельные и равные основания, а остальные грани (их называют боковы- ми) являются параллелограммами, имеющими общие стороны с основаниями.
Призмы и цилиндры |
285 |
Отpезoк, соединяющий две вершины призмы, не принадлежа- щие одной грани, называется диагональю npuзмы.
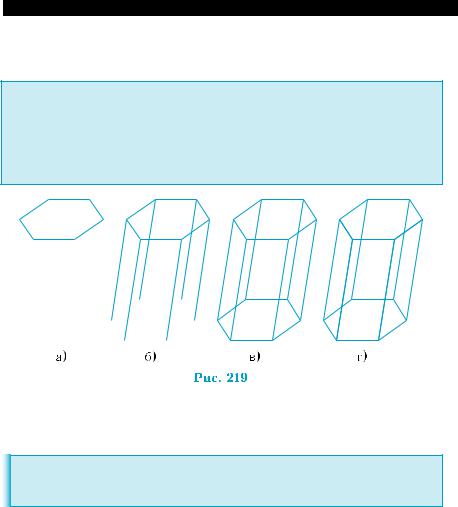
При изображении призм (как и при изображении пирамид) пользуются следующими правилами:
1)строят изображение верхнего основания призмы (рис. 219, а);
2)из вершин построенного многоугольника проводят образую-
щие (рис. 219, б);
3)строят изображение нижнего основания призмы, соединяя концы построенных образующих (рис. 219, в);
4)выделяют видимые и невидимые ребра (рис. 219, г).
Один из видов четырехугольных призм был рассмотрен в 10 классе, где речь шла о napaллeлenиneдах, тo есть o npuз-
мах, ocнoвaниямu которых являются napaллeлoгpaммы.
Параллелепипед — от греческих παραλληλοζ (paralle los) — параллельный и επιπεδοζ (epipedos) — равное, плоское.
Диагонали параллелепипеда обладают такими же свойствами, как и диагонали параллелограмма. Об этом идет речь в следую- щей теореме.
Teopeмa 1 (о свойствах диагоналей параллелепипеда).
Диагонали параллелепипеда пересекаются в одной точ ке и точкой пересечения делятся пополам. Эта точка яв ляется центром симметрии параллелепипеда.
Пусть дан параллелепипед ABCDA1B1C1D1. Проведем диа- гонали B1D и CA1 (рис. 220). Они являются диагоналями парал-
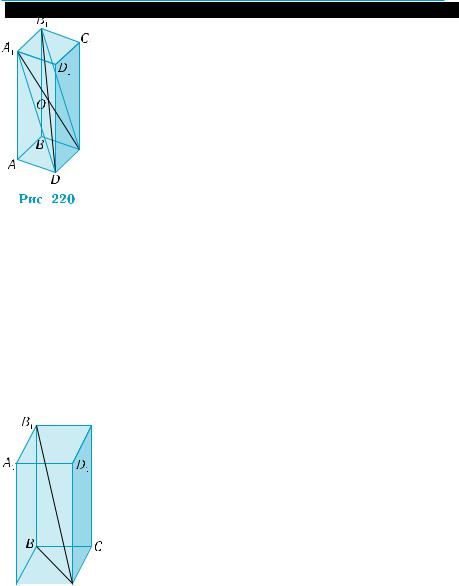
286 Раздел 5. Геометрические тела и поверхности
лелограмма DCB1A1 (DC || A1B1 и DC = A1B1). Обо- значим точку их пересечения через О. Диагонали B1D и CA1 делятся точкой О пополам. Аналогично
рассуждая по поводу всех пар диагоналей, придем к выводу, что их середины совпадают. То есть вер- шины параллелепипеда расположены симметрич- но относительно точки пересечения диагоналей. Отсюда вытекает, что относительно этой точки сим-
 метрично расположены ребра, грани параллелепи- педа и вообще весь параллелепипед.g
метрично расположены ребра, грани параллелепи- педа и вообще весь параллелепипед.g
Чаще всего применяются призмы, у которых  образующие перпендикулярны основанию, то есть прямые призмы. Высота прямой призмы равна длине образую- щей. Прямой параллелепипед, основанием которого является пря-
образующие перпендикулярны основанию, то есть прямые призмы. Высота прямой призмы равна длине образую- щей. Прямой параллелепипед, основанием которого является пря-
моугольник, называется прямоугольным параллелепипедом.
Длины трех ребер прямоугольного параллелепипеда, сходящиеся в одной вершине, называются его измерениями. Их еще называют длиной, шириной и высотой параллелепипеда при условии, что две противоположные грани выбраны в качестве оснований.
Теорема 2 (о свойствах диагоналей прямоугольного параллелепипеда).
В прямоугольном параллелепипеде квадрат длины любой диагонали равен сумме квадратов трех его измерений.
 В прямоугольном параллелепипеде ABCDA1B1C1D1 (рис. 221) рассмотрим диагональ DB1. Так как ребро ВВ1 перпендикулярно основа- нию ABCD, то из прямоугольного треугольника
В прямоугольном параллелепипеде ABCDA1B1C1D1 (рис. 221) рассмотрим диагональ DB1. Так как ребро ВВ1 перпендикулярно основа- нию ABCD, то из прямоугольного треугольника
BB1D имеем: B1D2 = BD2 + BB12 . Кроме того, диаго-
наль основания BD является гипотенузой прямо угольного треугольника BCD. Поэтому BD2 = CD2 +
+ BC2 иB1D2 = CD2 + BC2 + BB12 = AB2 + BC2+ BB12.g
Очевидным является родство доказанной тео 

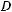 ремы с теоремой Пифагора, поэтому ее и назы-
ремы с теоремой Пифагора, поэтому ее и назы- 


 вают пространственной теоремой Пифагора. Из этой теоремы, в частности, вытекает, что диагонали прямоуголь-
вают пространственной теоремой Пифагора. Из этой теоремы, в частности, вытекает, что диагонали прямоуголь-
ного параллелепипеда равны между собой.
Большое практическое значение имеют правильные призмы.

Призмы и цилиндры |
287 |
Прямая призма называется правильной, если ее
основаниями являются правильные многоугольники.
Куб является правильной четырехугольной призмой, так как в его основании лежит квадрат, и куб является прямым паралле- лепипедом. Правильные призмы достаточно часто используются в технике, строительстве, так как разнообразные детали, конструкции имеют форму призмы, в частности, заготовки для гаек чаще всего имеют форму правильной шестиугольной призмы (рис.222, а), иног- да — треугольной, четырехугольной или восьмиугольной. Hepедкo форму призмы имеют башни, части сооружений (рис. 222, б–г).
Очeвиднo, что все боковые гpaни пpaвильнoй призмы являют- ся равными между coбoй пpямoугольникaми (почему?).
При изучении призм, как и при изучении других тел, важным является исследование сечений призм плоскостями. Обратим внимание на диагональ- ное сечение призмы. Речь идет о сечении призмы плоскостью, проходящей через два боковых ребра, не принадлежащие одной грани (рис. 223). Из па- раллельности оснований призмы вытекает, что диагональным сечением призмы является парал- лелограмм, а если плоскость сечения параллельна основаниям, то сечением является многоугольник,
равный основанию. Это обосновывается так же, как и равенство оснований.
П р и м е р 1 . Основанием прямого параллелепипеда является параллелограмм со сторонами 6 см, 8 см и острым углом 60°. Диагональ меньшей боковой грани образует с ребром основа- ния параллелепипеда угол 45°. Вычислить: 1) диагонали осно- вания; 2) высоту параллелепипеда; 3) диагонали параллеле-
288 |
Раздел 5. Геометрические тела и поверхности |
пипеда; 4) углы между диагоналями и плоскостью основания параллелепипеда; 5) площади диагональных сечений.
Пусть ABCDA1B1C1D1 — данный парал-  лелепипед, AD = 6 см, АВ = 8 см, DАВ = 60°,
лелепипед, AD = 6 см, АВ = 8 см, DАВ = 60°,
D1AD = 45° (рис. 224).
1) Из треугольника ABD по теореме коси- нусов имеем:
|
|
|
|
BD = |
82 + 62 − 2 6 8 cos60° = 2 13 (см). |
||||||||||||
|
|
|
|
Так |
|
как |
BD2 + AC2 |
= 2AD2 + 2AB2 , то |
|||||||||
|
|
|
AC = 2 37 см. |
|
|
|
|
|
|
||||||||
|
|
|
|
2) Высота параллелепипеда равна DD1. |
|||||||||||||
|
|
|
Треугольник |
DD1А – прямоугольный равно- |
|||||||||||||
бедренный, D1D ^ AD, D1AD = 45°. Поэтому DD1 |
= АD = 6 см. |
||||||||||||||||
|
3) Диагонали параллелепипеда являются гипотенузами прямо- |
||||||||||||||||
угольных треугольников ВDD1 и АСС1, в которых известны катеты. |
|||||||||||||||||
Из этих треугольников, пользуясь решением задания 1), получим: |
|||||||||||||||||
|
BD = |
BD2 + DD2 |
= |
52 + 36 = 2 |
22 (см); |
|
|
|
|
|
|||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
AC = |
AC2 + CC2 |
= |
148 + 36 = 2 |
46 (см). |
|
|
|
|
|
|||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
углами D1ВD |
|||
|
4) Упомянутые в условии углы измеряются |
||||||||||||||||
и С1АС. |
tg D BD = DD1 |
|
3 |
|
|
|
|
|
|
3 |
|
||||||
|
|
= |
, |
D BD = arctg |
|
|
, |
||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
1 |
|
DB |
|
13 |
|
|
1 |
|
|
|
13 |
|
|||
|
|
|
|
|
3 |
|
|
|
3 |
|
|
||||||
|
|
|
tg C AC = |
|
|
, C AC = arctg |
. |
|
|||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
1 |
|
|
|
37 |
|
|
|
1 |
|
37 |
|
|
|
||
5) Диагональными сечениями параллелепипеда являются пря- |
|||||||||||
моугольники |
АА С С и DBB D . Стороны их найдены раньше, поэто- |
||||||||||
|
|
|
|
1 |
1 |
1 |
1 |
|
см2 и 12 13 см2. g |
||
му их площади равны, соответственно, 12 37 |
|||||||||||
Ответ. 1) 2 13 см; 2 37 см; 2) 6 см; 3) 2 |
22 см, 2 |
46 см; |
|||||||||
4) arctg |
|
3 |
, |
arctg |
3 |
; 5) 12 37 |
см2, 12 13 |
см2. |
|
||
|
13 |
37 |
|
||||||||
Пример |
2. |
В |
прямоугольном |
параллелепипеде |
измерения |
||||||
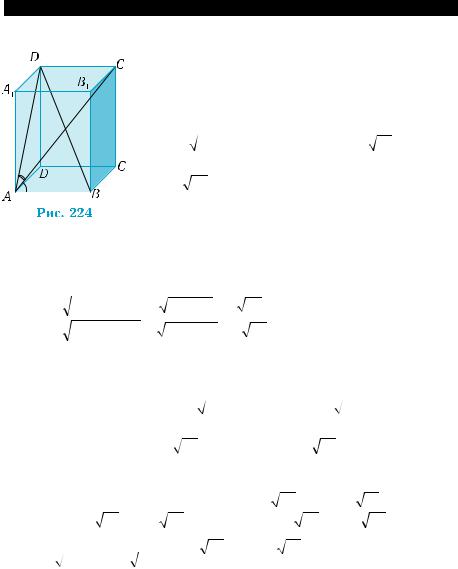
равны 1 см, 1 см и 2 см. Вычислить: 1) диагонали параллелепипе- да; 2) углы между диагоналями.
Пусть ABCDA1B1C1D1 — прямоугольный параллелепипед,
AВ = ВС = 1 см, АА1 = 2 см (рис. 225).
Призмы и цилиндры |
289 |
|
1) Согласно пространственной теореме Пи- |
|
|
|
|
|
|
|
|
||||||||||||||||||||
фагора, |
AC = |
12 + 12 + 22 |
= |
|
6 (см). Все диа- |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гонали равны |
6 см. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2) Речь идет об углах между диагоналями |
|
|
|
|
|
|
|
|
||||||||||||||||||||
АС1 и BD1 и между |
АС1 и |
А1С (остальные ва- |
|
|
|
|
|
|
|
|
|||||||||||||||||||
рианты аналогичны). Если О |
— центр симме- |
|
|
|
|
|
|
|
|
||||||||||||||||||||
трии параллелепипеда, О1 |
— центр симме- |
|
|
|
|
|
|
|
|
||||||||||||||||||||
трии верхней грани, то в равнобедренном |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
треугольнике |
А |
С |
О имеем: |
|
|
A O |
= |
6 |
|
см, |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
1 |
1 |
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1O1 |
|
|
|
1 |
|
|
|
||||||
A C = |
2 см, A OC = 2 A OO = 2arcsin |
= 2arcsin |
. Ана- |
||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
1 |
1 |
|
|
1 |
1 |
1 |
|
1 |
|
|
|
|
|
|
A1O |
|
|
|
3 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
логично, из треугольника D |
OC |
1 |
имеем: |
D OC = 2arcsin |
1 |
|
. g |
||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
6 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||
|
Ответ. 1) |
6 см; 2) 2arcsin |
|
|
, 2arcsin |
. |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Рассмотрим построение изображений сечений призм |
|||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
с использованием прямой пересечения секущей пло- |
|||||||||||||||||||||||||
|
|
|
|
скости с плоскостью одного из оснoваний. Эту прямую |
|||||||||||||||||||||||||
|
|
|
|
нaзывaют cледoм секущей nлoскости. |
Отметим, |
||||||||||||||||||||||||
что сечением призмы плоскостью является мнoгoугольник, а его |
|||||||||||||||||||||||||||||
cтopoны—этоотрезки,покоторымдaннaяплоскостьпepeсекаетгpa- |
|||||||||||||||||||||||||||||
ни. Понятно, что чиcлo cтоpон сечения не пpeвышает чиcлa гpaнeй |
|||||||||||||||||||||||||||||
призмы, a вepшинaми сечения являются точки пepeсечения секу- |
|||||||||||||||||||||||||||||
щей плоскости с pебpaми призмы. Таким образом, для построения |
|||||||||||||||||||||||||||||
сечения достаточно найти точки пересечения секущей плоскости с |
|||||||||||||||||||||||||||||
pебpaми призмы. Эти точки будут |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
вepшинами искомoгo мнoгoуголь- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
никa, являющегося сечением при- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
змы плоскостью. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пусть имеем призму, след а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
секущей плоскости, принадлежа- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
щий плоскости одного из основа- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ний, и точку |
M |
на поверхности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
призмы, через которую проходит |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
секущая плоскость. Допустим, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
что точка M лежит на другом ос- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
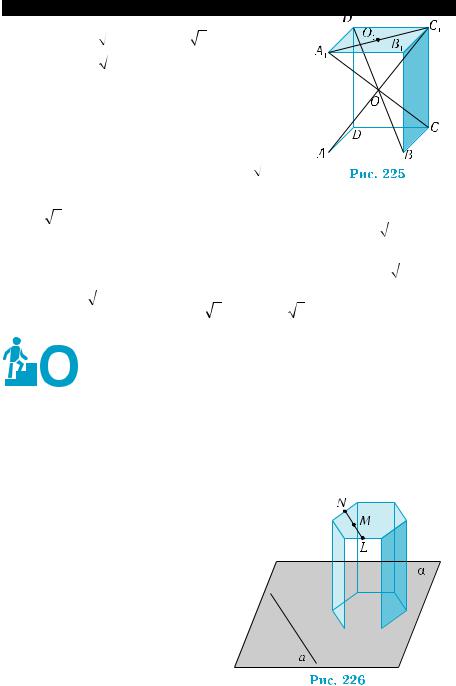
новании призмы (рис. 226). Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
290 |
Раздел 5. Геометрические тела и поверхности |
секущая плоскость пересекает это основание по отрезку NL пря- |
|
мой, параллельной прямой а (почему?), и проходит через точку |
|
M. Следовательно, проведя через точку M прямую, параллельную |
|
прямой а, до пересечения со сторонами основания, которому при- |
|
надлежит точка M, мы найдем две вершины N и L искомого сече- |
|
ния. Построение остальных вершин описано ниже. |
|
|
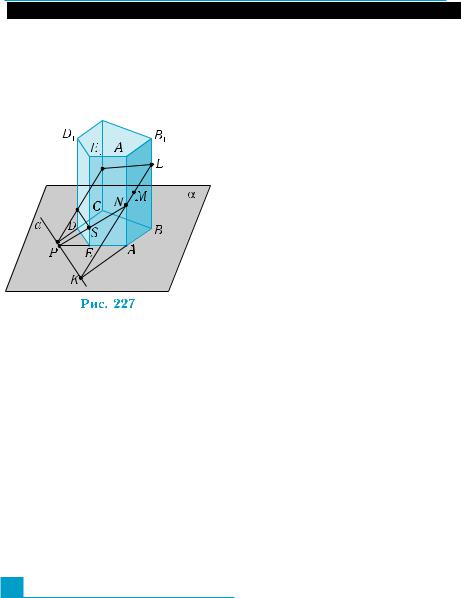
Рассмотрим случай, когда точ- |
|
ка M расположена на боковой |
|
грани ABB1A1 (рис 227). Построим |
|
сначала точку K, в которой пере- |
|
секаются плоскость этой грани и |
|
прямая а. Для этого достаточно |
|
продолжить ребро AB, лежащее |
|
в одной плоскости с прямой а, до |
|
пересечения с прямой а. Прямая |
|
KM пересекает стороны паралле- |
|
лограмма ABB1A1 в точках N и L, |
|
которые и являются двумя вер- |
|
шинами сечения (почему?). |
Аналогично строится точка S как точка пересечения ребра ЕЕ1 с |
|
прямой NP, где Р – точка пересечения прямыхАЕ и а (см. рис. 227). |
|
Пусть в данном примере прямая а параллельна ребру DE. Тогда, |
|
проведячерезточкуS прямую,параллельнуюа,допересечениясре- |
|
бром DD1, найдем пересечение секущей плоскости с граньюEE1D1D. |
|
Остальные вершины сечения строятся по указанному алгоритму. |
|
Если след секущей плоскости не задан, а плоскость определе- |
|
на, например, тремя точками, принадлежащими призме, то не- |
|
обходимо сначала построить ее след в плоскости какого-нибудь |
|
основания. Вернемся к рис. 227. Если бы секущая плоскость опре- |
|
делялась точками |
S, M, L, то две точки ее следа в плоскости a |
можно найти как точки пересечения прямых LS, BE и ML, AB. |
|
Рассмотренный метод построения сечений называют мето- |
|
дом следов. |
|
99 Контрольные вопросы
1°. Сколько ребер имеет пятиугольная призма?
2°. Может ли призма иметь нечетное число вершин? 3. Может ли призма иметь четыре грани?
4. Будет ли сечение, перпендикулярное боковому ребру призмы, перпендикулярным и ее боковой грани?
