978-966-10-2413-6_Matematuka 11_rus
.pdf
Применение интеграла |
241 |
скорость, моль/(с м3); t — время, с. Как изменится концентрация вещества за время от t1 = 0 до t2 = 5 с?
Если c(t) — концентрация вещества в момент времени t, то c′(t) = v(t) = 3t +1 . Нужно найти приращение функции c(t) на про- межутке [0;5] . Согласно приведенной формуле, имеем
c(5) − c(0) |
5 |
5 |
|
3t |
2 |
|
|
5 |
|
||||||||
= ∫v(t)dt =∫(3t + 1)dt = |
|
+ t |
|
= 42,5 (моль/м3).g |
||||
|
0 |
0 |
|
2 |
|
|
0 |
|
Ответ. 42,5 моль/м3. |
|
|
|
|
|
|
||
Вторая схема применения интеграла основывается 
на том, что интеграл равен пределу интегральных сумм (см. § 10). Исследуемую величину прибли- женно представляют в виде интегральной суммы с
дальнейшим предельным переходом. Это метод мы уже использо- вали при нахождении площади криволинейной трапеции в §10. Теперь с его помощью решим задачу на нахождение работы пере- менной силы.
Задача (работа переменной силы ). Материальная точка движется по оси х под действием силы у = F(x) , направленной
вдоль этой прямой. Найти работу силы по перемещению точки из положения х = а в положение х = b.
Если материальная точка движется по оси х под действием постоянной силы F, то работа А по перемещению точки из положе- ния х = а в положение х = b равна
A = F(b − a) .
Если же движение проходит под действием переменной силы, то для решения поставленной задачи применяют интегральные методы.
Разобьем отрезок [a;b] точками a = x0 < x1 < < xn = b на п равных отрезков длиной x = b −n a . На каждом из этих отрезков
[xi −1 ,xi ], i = 1,2, ,n , сила изменяется мало. Поэтому приближен-
но ее можно считать постоянной, равной, например, F(xi–1). Тогда работа, совершаемая силой на отрезке [xi −1 , xi ] , приближенно рав-
на F (xi −1 ) x , а работа силы на всем отрезке [a;b] приближенно равна
242 Раздел 4. Интеграл и его приложения
A ≈ (F(x0 ) + F(x1 ) + ... + F(xn−1 )) x.
Перейдя в последнем равенстве к пределу при п → ∞, получим:
b
A = ∫ F(x)dx . g
Пример 8. Какую работуa надо произвести, чтобы растянуть пружину на 3 см, если сила в 10 Н растягивает пружину на 1 см?
ПозаконуГука,силаF,растягивающаяпружину,пропорцио нальна перемещению х свободного конца пружины, то есть F = kx. Для нахождения коэффициента k воспользуемся тем, что сила в 10 Н растягивает пружину на 0,01 м: 10 = 0,01k, k = 1000.
|
|
|
|
|
|
b |
Тогда F = 1000x и работу находим по формуле A = ∫ F(x)dx : |
||||||
|
|
|
|
|
|
a |
|
0,03 |
1000x dx = 1000 x |
2 |
|
0,03 |
|
|
|
|||||
|
A = ∫ |
|
|
= 0,45 (Дж). g |
||
|
0 |
2 |
|
0 |
||
|
Ответ. 0,45 Дж. |
|
|
|
||
|
Контрольные вопросы |
|
|
|
||
99 |
|
|
|
|||
1°. |
|
|
|
|
|
b |
Каков физический смысл формулы: ∫ f (x)dx = f (b) − f (a) ? |
||||||
|
|
|
|
|
|
′ |
2.Первообразной для какой величиныa является: а) закон дви- жения; б) скорость движения?
3.Известно, что сила тока I изменяется со временем t по закону I = I(t). Выразите с помощью интеграла заряд q, проходящий через поперечное сечение проводника за промежуток време- ни [t0; T], если известно, что I(t)= q′ (t).
Задачи
206°. Найдите площадь фигуры, ограниченной линиями:
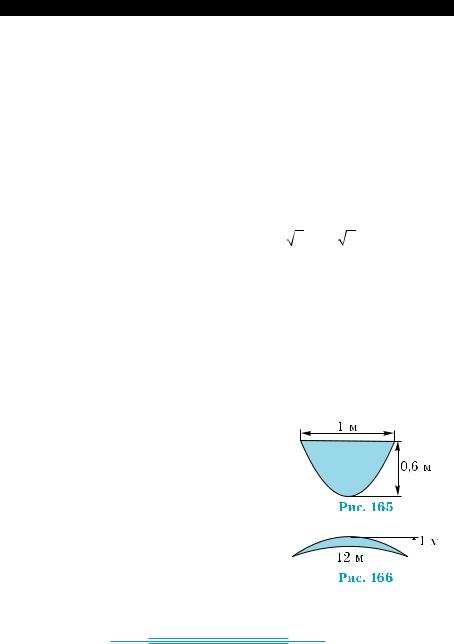
1) у = |
x , у = 0, х = 4; |
|
|
2) |
у = х2 + 1, у = 0, х = –2, х = 2; |
|
3)у= (х + 1)2,х= 0, |
х= –2,у= 0; |
4) |
у = ех + 1, у = 0, х = –1, х = 1; |
|||
5) у = х2 – 1, у = 0; |
|
|
|
6) у = − 6 , х = 1, х = е, у = 0; |
||
|
|
|
π |
|
π . |
x |
7) y = cos x, y = 1, |
x = − |
, x = |
|
|||
|
|
|
2 |
|
2 |
|
Применение интеграла |
|
|
|
|
243 |
|
|
207. Найдите площадь фигуры, ограниченной линиями: |
|||||||
1) |
|
π |
≤ x ≤ |
7π |
7π |
; |
|
y = cos x, |
2 |
, y = 0, x = |
4 |
|
|||
|
|
|
4 |
|
|
||
2) |
y = e−x −1, y = 0, x = 1, x = −1 ; |
|
|
|
|||
3) |
y = −x2 + 2x +10, y = 10 ; |
|
|
|
|||
4) |
y = sin x, y = 2sin x (0 ≤ x ≤ π) ; |
|
|
|
|||
5)y = x2 , x + y = 2 ;
6)y = sin x, y = 2sin x (−π ≤ x ≤ π) ;
7)y = 2x2 , y = x2 +1 ;
8) y = sin x, y = cos x |
|
− |
3π |
≤ x ≤ |
π |
; |
|
|
4 |
4 |
|
||||
|
|
|
|
|
|
||
9) y = 2x , y = −2x , x = 0, x = 1 ; |
10) |
y = x , y = 3 x ; |
|
11) y = x2 , x + y = 2, y = 0 ; |
12*) |
y = sin x, y = x2 − πx . |
|
208*. Найдите |
площадь фигуры, ограниченной гиперболой |
||
y = − 1 , касательной к ней, проведенной в точке с абсциссой |
|||
x |
|
|
|
х = 1, и прямой х = 2. |
|
|
|
209*. Функция |
у = F(x) является первообразной для функции |
||
f(x) = 2x – 4. Найдите площадь фигуры, ограниченной гра- |
|||
фиками функций у = f(x) и |
у = F(x), зная, что график фун- |
||
кции у = F(x) проходит через точку А(0; 4). 210*. Найдите площадь поперечного сече-
ния канала для орошения, имеюще- го форму параболического сегмента
(рис. 165).
211*. Серповидная опора, у которой верх ний и нижний контуры являются
параболами (рис. 166), изготовле- на из 10-миллиметрового плоско-
го стального листа. Найдите массу 
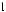
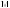этой опоры по формуле m = rSd, где 
r = 7,8 103 кг/м3 — плотность стали, S — площадь сечения опоры, d — ее
толщина.
212.Скорость тела, движущегося прямолинейно, изменяется по за- кону v = 2 + t − t2 , где v — скорость, м/с;t — время, с. Найдите:
244 Раздел 4. Интеграл и его приложения
1°) перемещение тела за промежуток времени [1; 3]; 2) путь, пройденный телом за промежуток времени [1; 3].
213°. Колесо вращается с угловой скоростью, изменяющейся по |
||
закону ω = 2t + 3 , где w — угловая скорость, рад/с; t — вре- |
||
мя, с. На какой угол повернется колесо за промежуток вре- |
||
мени [1; 5]? |
по закону |
|
214°. Скорость |
нагревания жидкости изменяется |
|
v = 0,2t + 1 |
, где v — скорость нагревания, К/с; t |
— время, с. |
На сколько кельвинов нагреется жидкость за первые 3 с? 215°. Скорость изменения температуры жидкости v в зависимости
от времени t выражается формулой v = 3t – 2 (температура измеряется в °С, время — в секундах). На сколько градусов изменится температура жидкости за промежуток времени
[1; 4]?
216*. Точка совершает гармоническое колебание со скоростью v = 3sin 8π t , где v — скорость, м/с; t — время, с. Найдите:
1) перемещение точки за промежуток времени [0; 16]; 2) путь, пройденный точкой за промежуток времени [0; 16].
217. При сжатии пружины на 2 см произвели работу в 40 Дж. Какую работу нужно произвести, чтобы растянуть пружину на 3 см?
218*. Два единичных электрических заряда расположены на рас- стоянии 5 см друг от друга. Затем один из зарядов освобо- ждается и удаляется от другого под действием силы оттал-
кивания, которая по закону Кулона имеет вид F = rk2 , где
r — расстояние между зарядами, k – коэффициент пропор- циональности. Какую работу выполняет сила, если заряд удалится на расстояние: 1) 10 см; 2) 15 см?
Применение интеграла |
245 |
|
|
||||
|
|
|
|
|
Итог |
||
|
|
|
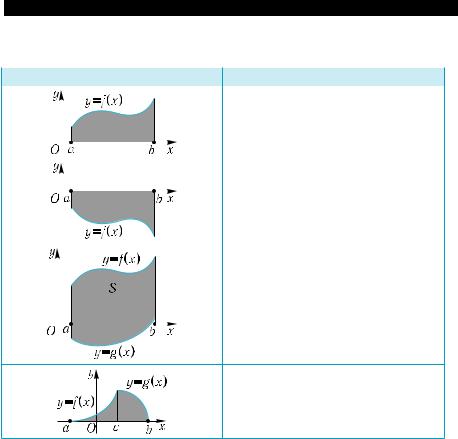
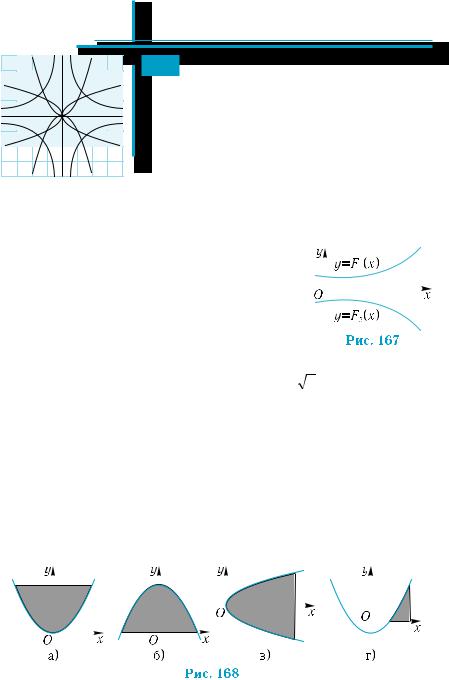
Вычисление площадей плоских фигур |
||||
|
|
|
|
|
|
|
|
|
|
|
Фигура |
|
Площадь |
||
|
|
|
|
|
b |
||
|
|
|
|
|
S = ∫ f(x)dx |
||
|
|
|
|
|
a |
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
||
|
|
|
|
|
S = −∫ f(x)dx |
||
|
|
|
|
||||
|
|
|
|
|
a |
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
||
|
|
|
|
|
S = ∫( f(x) − g(x))dx |
||
|
|
|
|
|
a |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
b |
S = ∫ f (x)dx + ∫ g(x)dx |
|
a |
c |
1 |
Готовимся к тематиче - |
|
скому оцениванию по |
|
теме «Интеграл и его |
|
приложения» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задания для самоконтроля |
|||||||||||||||||
?? |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1°. |
|
Может ли функция иметь лишь конечное |
||||||||||||||||||
|
|
|
число первообразных? |
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||||||
2°. |
|
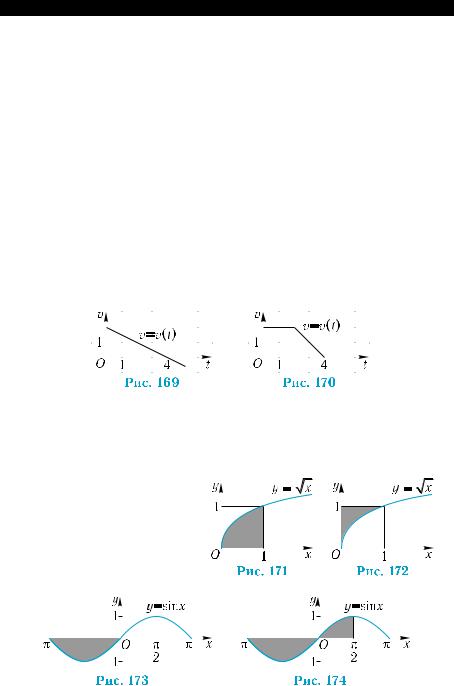
Могут ли функции, графики которых изо- |
|
|
|
|
||||||||||||||
|
|
|
бражены на рис. 167, быть первообразны- |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
ми для одной функции? |
|
|
|
|
|||||||||||||
3°. |
|
Найдите первообразные для функции |
|
|
|
|
||||||||||||||
|
|
|||||||||||||||||||
|
|
|
у = 1 на промежутке (0; ∞). |
|||||||||||||||||
|
|
|
x |
|||||||||||||||||
4°. |
|
Найдите первообразную для функции у = x , график которой |
||||||||||||||||||
|
|
|
проходит через точку А(9; 1). |
|||||||||||||||||
5°. |
|
Скорость тела, движущегося прямолинейно, задается форму- |
||||||||||||||||||
|
|
|
лой v = 2sin t + 1. Найдите закон движения этого тела, если в |
|||||||||||||||||
|
|
|
начальный момент времени (t = 0) тело имело координату –1. |
|||||||||||||||||
6. |
|
|
Известно, что функция у = F(x) является первообразной для |
|||||||||||||||||
|
|
|
функции у = f(x). Какие из функций: а) у = F(x + 2); б) у = F(x) + |
|||||||||||||||||
|
|
|
+ 2; в) у = 2F(x); г) у = F(2x) обязательно являются первообраз- |
|||||||||||||||||
|
|
|
ными для данной функции? |
|||||||||||||||||
7°. |
|
Какие из фигур, изображенных на рис. 168, а)–г), являются |
||||||||||||||||||
|
|
|
криволинейными трапециями? |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Готовимся к тематическому оцениванию по теме |
247 |
8.Чему равен интеграл:
|
|
3 |
0 |
|
b |
если f (b) = f (a) ; |
|||
а°) ò f (x)dx , если ∫ f (x)dx = −1 ; б) |
∫ f (x)dx, |
||||||||
|
|
|
|
|
′ |
|
|
|
|
|
|
0 |
3 |
|
a |
|
|
|
|
|
− |
π |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
в) |
∫ sin2 xdx ? |
|
|
|
|
|
|
|
|
|
− |
π |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
9°. Верно ли равенство: |
|
|
|
|
|
|
|||
|
1 |
|
|
1 |
|
−1 |
|
|
|
а) |
∫dx = 1; |
б) |
∫ ex dx = e−1 |
− e ; в) |
∫ dx |
= ln x |
|
−−1e ? |
|
|
|||||||||
|
0 |
|
|
−1 |
3 |
−e x |
|
|
|
10.Каков геометрический смысл интеграла ò2dx ?
11.Какой путь прошла материальная точка 0за промежуток вре- мени [0; 4], если она движется вдоль координатной прямой со скоростью v = v(t), график которой изображен на: 1) рис. 169; 2) рис. 170?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12°.Точка движется прямолинейно со скоростью v = t2 |
+ 1. Какой |
|||||||||||||||||||||||||||||||||||
|
путь она прошла за промежуток времени [0; 3]? |
|
|
|
|
|||||||||||||||||||||||||||||||
13. |
Изобразите фигуру, ограниченную линиями: |
|
|
|
|
|||||||||||||||||||||||||||||||
|
а) у = 2х, у = 2, х = 0; |
|
|
б) у = х2, у = х + 1. |
|
|
|
|
||||||||||||||||||||||||||||
14. |
Чему равна площадь фи- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
гуры, изображенной на: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
а°) рис. 171; б°) рис. 172; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
в°) рис. 173; г) рис. 174? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
248 |
Раздел 4. Интеграл и его приложения |
||||
Ответы к заданиям для самоконтроля |
|
||||
1. Нет. 2. Нет. 3. |
у = ln x + C. 4. y = |
2 |
3 |
|
|
3 |
x 2 −17 . 5. x = –2cos t + |
||||
+ t – 1. 6. б). 7. б), г). 8. а) 1; б) 0; в) 0. |
Правильным является |
||||
9. |
|||||
лишь равенство а).10. Площадь прямоугольника, изображен- |
|||||
ного на рис. 175.11. а) 4; б) 6.12. 12. |
14. а) 2 ; б) |
1 ; в) 2; г) 3. |
|||
|
|
|
3 |
3 |
|
Образец контрольной работы №4
1.Вычислите интеграл:
|
π |
|
|
1 |
|
|
|
|
1 |
|
|
|
4 |
1 |
|
|
|
2 |
|
|
|
||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1°) |
∫0 |
|
|
|
|
|
− |
|
dx ; |
2°) |
|
|
|
|
+ |
|
dx ; |
|
|||||
|
|
2 |
x |
|
|
x |
x |
|
|||||||||||||||
|
2cos |
|
|
|
π |
|
|
∫1 |
|
|
|
|
|
|
|||||||||
|
4 |
|
x − x + 2 |
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|||||||
3) |
∫ |
|
dx ; |
|
4*) |
∫(1 + tg2 2x )dx . |
|
||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
1 |
|
|
|
x |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
2°. Скорость мяча, брошенного с поверхности земли вертикально |
|||||||||||||||||||||||
вверх, изменяется по закону v = 15 – gt, где v — скорость, м/с; |
|||||||||||||||||||||||
t — время, с; g ≈ 10 м/с2 — ускорение свободного падения. На |
|||||||||||||||||||||||
какую высоту поднимется мяч за первую секунду? |
|
||||||||||||||||||||||
3. Вычислите площадь фигуры, ограниченной линиями: |
|||||||||||||||||||||||
1°) |
у = х2 – 1, |
у = |
0, х = 1, х = 3; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2) у = х2 |
– 1, у = 0, х = 3; |
|
|
0. |
|
|
|
|
|
|
|
||||||||||||
3*) у = х2 – 1, |
у = sin px (0 ≤ х ≤ 1), х = |
|
|
|
|
|
|
|
|||||||||||||||
Интеграл, его геометрический и физический смысл |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 36 |
|
Определение |
|
Геометрический |
|
|
|
Физический |
|||||||||||||||||
интеграла |
|
|
смысл |
|
|
|
|
|
|
|
|
смысл |
|||||||||||
b |
|
|
|
|
|
|
|
|
|
|
|
Если f(x) |
≥ |
0, |
|
то |
Если |
f(t) |
≥ 0, то |
||||
∫ f(x)dx = F(b) − F(a) , |
b |
|
|
|
|
|
|
|
T |
|
|
|
|||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
ò f (x)dx — площадь |
|
ò f (t)dt — путь, про |
|||||||||
где у = F(x) — перво |
a |
|
|
тра- |
|
|
t0 |
|
|
|
|||||||||||||
образная |
для |
|
функ- |
криволинейной |
|
йденный точкой, дви- |
|||||||||||||||||
ции у = f(x). |
|
|
|
|
|
|
пеции, ограниченной |
|
жущейся |
прямоли- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
графиком |
функции |
|
нейно |
со |
скоростью |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
у = f(x) и отрезками |
|
v =f(t), за промежуток |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
прямых у = 0, |
х = а, |
|
времени [t0;T]. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
х= b. |
|
|
|
|
|
|
|
|
|
|
|
Готовимся к тематическому оцениванию по теме |
|
|
|
249 |
|
|
|||
|
Свойства интеграла |
Таблица 37 |
|||||||
|
|
|
|
|
|
|
|||
Словесная формулировка |
Символическая запись |
|
|||||||
Интеграл от суммы функций |
b |
|
|
b |
b |
|
|
||
равен сумме |
интегралов |
от |
∫( f (x) + g(x))dx = ∫ f (x)dx +∫ g(x)dx |
|
|||||
этих функций. |
|
a |
|
|
a |
a |
|
||
Постоянный множитель мож |
b |
|
b |
|
|
|
|||
но выносить за знак интегра- |
∫ kf (x)dx = k∫ f (x)dx |
|
|||||||
ла. |
|
|
a |
|
a |
|
|
|
|
Если с — некоторая точка |
b |
c |
|
|
b |
|
|
||
отрезка [a;b] , то интеграл от |
∫ f (x)dx = |
∫ f (x)dx + ∫ f (x)dx |
|
||||||
функции на |
промежутке |
a |
a |
|
|
c |
|
||
[a;b] равен сумме интегра- |
|
|
|
|
|
|
|
||
лов от той же функции на |
|
|
|
|
|
|
|
||
промежутках [a; c] и [c;b] . |
|
|
|
|
|
|
|
|
|
Производная и интеграл в прикладных задачах |
|||||||||
|
|
|
|
|
|
|
Таблица 38 |
||
Величина |
Производная |
|
Интеграл |
|
|||||
s — перемещение |
|
ds |
|
|
|
t2 |
|
|
|
v — скорость |
|
|
v(t) = dt |
|
|
|
s = ∫v(t)dt |
|
|
|
|
|
|
|
|
|
t1 |
|
|
q — электрический заряд |
|
I(t) = dq |
|
|
|
t2 |
|
|
|
I — сила тока |
|
|
|
|
|
q = ∫ I(t)dt |
|
||
j — угол поворота шкива |
|
dt |
|
|
|
t |
|
||
|
dϕ |
|
|
|
t21 |
|
|||
w — угловая скорость |
|
ω(t) = dt |
|
|
|
ϕ = ∫ω(t)dt |
|
||
|
|
|
|
|
|
|
t1 |
|
|
А — работа |
|
|
dA |
|
|
x2 |
|
|
|
F — сила |
|
|
F(x) = dx |
|
|
A = ∫ F(x)dx |
|
||
|
|
|
|
|
|
|
x1 |
|
|
Исторический комментарий
Идеи интегрирования возникли при вычислении площадей произвольных плоских фигур и площадей поверхностей и объе- мов тел почти 2,5 тыс. лет тому назад. Наибольших успехов при решении таких задач достиг Архимед (ок. 287–212 гг. до н. э.). Его рассуждения связаны с решением конкретных геометрических задач. Например, Архимед вычислил площадь параболическо- го сегмента, площадь поверхности и объем шара, сегментов тел, ограниченных поверхностью вращения параболы, гиперболы и плоскостью, и много др. И хотя с позиций современной математи- ки некоторые вычисления почти тождественны, то есть сводятся к похожим интегралам, Архимед их различает, проводя рассужде- ния в каждом конкретном случае сначала. То есть Архимед не создал исчисления, а лишь построил основы для его создания.
Творцами учения об интеграле были И. Ньютон (1643–1727) и независимо от него Г. Лейбниц (1646–1716). Они объединили дифференциальное и интегральное исчисление, доказав форму- лу, носящую их имена, показали могущество своих методов, ре- шив большое количество физических и геометрических задач.
В течение трех веков учение об интеграле развивалось и совер- шенствовалось. Усложнялись, исходя из практических проблем, множества, на которых определялась подынтегральная функция, расширялся класс интегрируемых функций. Все это вело к обобще- нию понятия интеграла, увеличению класса задач, где он приме- нялся. Так, с введением в математику переменных величин, введе- нием производной и первообразной функции появился новый тип уравнений, дающих возможность устанавливать различные виды функциональных зависимостей между величинами. Речь идет о дифференциальных уравнениях, рассмотрение которых началось в XVII ст. Главным «потребителем» таких уравнений была физика.
Большой вклад в развитие дифференциальных уравнений внесли выдающиеся украинские математики М.П. Кравчук
(1892–1942), Н.Н. Боголюбов (1909–1992), Ю.А. Митропольский (1917–2008), Я.Б. Лопатинский (1906–1981) и многие другие.