
978-966-10-2413-6_Matematuka 11_rus
.pdf
Kоординаты и иx применение |
121 |
Итог
Основные определения
Прямоугольными координатами точки М пространства называют координаты проекций М(х; у; z) точки М на оси координат, взятые в порядке нуме- рации осей.
Координатами вектора a в прямоугольной сис-
теме координат называют коэффициенты в его раз- a = (х; у; z) ложении по ортам i , j , k : a = xi + yj + zk .
Фигуру, составленную из всех точек M простран- ства, расстояния R от которых до заданной точки О одинаковы, называют сферой.
Основные утверждения
Координаты вектора AB вычисляются по формуле
AB = (x2 − x1 ; y2 − y1 ; z2 − z1 ) , где A(x1; у1; z1), В(x2; у2; z2). a = (x; y;z)
a = x2 + y2 + z2 .
Расстояние d между точками M1(х1; у1; z1) и М2(x2; у2; z2) вычи- сляется по формуле
d = (x2 − x1 )2 + (y2 − y1 )2 + (z2 − z1 )2 .
Для вычисления угла j между двумя ненулевыми векторами a1 = (x1 ; y1 ; z1 ) и a2 = (x2 ; y2 ; z2 ) используют формулу
cos ϕ = |
|
x1x2 + y1 y2 + z1z2 |
|
. |
|||
x 2 |
+ y 2 |
+ z 2 |
x 2 |
+ y 2 |
+ z 2 |
||
1 |
1 |
1 |
2 |
2 |
2 |
|
|
Ненулевые векторы a1 = (x1 ; y1 ; z1 ) |
и a2 = (x2 ; y2 ; z2 ) перпендику- |
||||||
лярны тогда и только тогда, когда x1x2 + y1 y2 + z1z2 = 0. |
|||||||
Beктop a1 = (x1 ; y1 ; z1 ) |
коллинеарен |
ненулевому вектору |
|||||
a2 = (x2 ; y2 ; z2 ) тогда и только тогда, когда существует такое чи-
сло l, что x1 = λx2 ; y1 = λy2 ; z1 = λz2 .
Уравнение (x − a)2 + (y − b)2 + (z − c)2 = R2 является уравнением
сферы с центром в точке (а; b; c) и радиуса R.
Уравнение ах + by + cz + d = 0 является уравнением плоскости, если не все коэффициенты а, b, c равны нулю.

Готовимся к тематиче - скому оцениванию по теме «Векторы и координаты»
?? Задания для самоконтроля
1°. Верно ли, что вершины параллелограмма задают 12 различ- ных ненулевых векторов?
2°. Является ли четырехугольник АBCD параллелограммом, если AB = DC ?
3.Является ли условие коллинеарности векторов AB и CD не- обходимым для параллельности прямых АВ и СD?
4.Верно ли, что a + b > a ?
5.Следует ли из неравенства k < 1 неравенство kc < c ?
6°. Верно ли, что если (a + b)(a − b) = 0 , то a = b ?
7.Перпендикулярны ли прямые АВ и АС, если
|
|
2 |
|
|
? |
(AB |
+ AC) |
|
= ( AB |
− AC)2 |
8.Обязательно ли тело будет двигаться, если на него действуют три равные силы?
Верно ли, что расстояние от точки М(–2; 3; 1) до плоскости ху меньше расстояния от этой точки до начала координат?
10°.Симметричны ли точки А(a;b; −c) и В (−a;b;c) относительно
плоскости ху?
11. Изменятся ли координаты точек на противоположные, если направления всех координатных осей изменить на противо- положные?
12°.Верно ли, что скалярная проекция вектора a = (−5;1; −3) на ось х равна 5?
13°.Верно ли, что векторы a = (2;4;2) и b = (1;2;1) коллинеарны? 14°.Противоположны ли векторы a = (5; −4;1) и b = −5i + 4 j − k ?
15°.Перпендикулярны ли векторы a = (1;2;3) и b = (1; −2;1) ?
16. Верно ли, что уравнение у = –1 в пространстве задает прямую?
Готовимся к тематическому оцениванию по теме |
123 |
17.Верно ли, что уравнение x2 + y2 + z2 + 2 = 0 является уравне- нием сферы?
Ответы к заданиям для самоконтроля
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Нет |
Да |
Да |
Нет |
Нет |
Да |
Да |
Нет |
Да |
Нет |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
|
|
Да |
Нет |
Нет |
Да |
Да |
Нет |
Нет |
|
|
|
Образец контрольной работы №2
Даны точки А(1; 1; –2), В(–3; 5; 1), С(4; 5; –1).
1°) Найдите координаты точки, симметричной точке С относи- тельно плоскости ху.
2°) Вычислите расстояние от точки В до плоскости хz. 3°) Вычислите длину отрезка АВ.
4°) Найдите координаты вектора 2AB − BC .
5) Вычислите длину вектора QC , если BQ = 3AQ . |
|
|||||
6) Составьте уравнение сферы с центром в точке В: |
|
|||||
а°) радиуса 3; б) проходящей через середину отрезка |
|
|||||
7) Составьте уравнение плоскости, проходящей через |
С |
|||||
перпендикулярно прямой BС. |
|
|
||||
8*) Исследуйте взаимное расположение сферы и плоскости, |
||||||
определенных в заданиях 6) и 7). |
|
|
||||
|
Векторное исчисление |
Таблица 17 |
||||
|
|
|
|
|
||
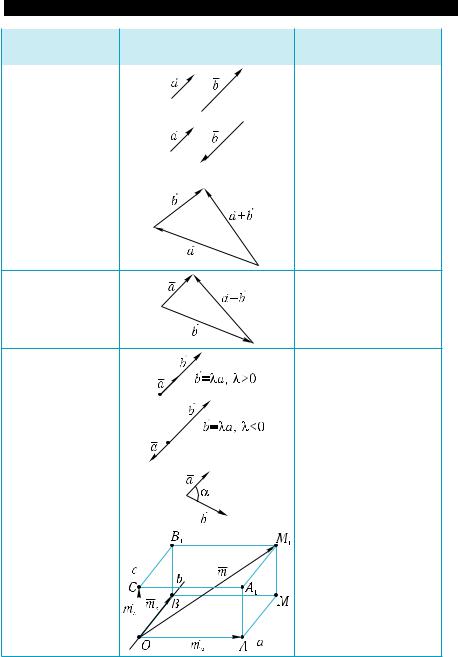
Понятие |
Геометрическая |
|
Символическая |
|
||
иллюстрация |
|
запись |
|
|||
|
|
|
||||
Вектор |
|
|
|
|
a |
|
|
|
|
|
|
|
|
Противополож- |
|
|
|
|
a и −a |
|
ные векторы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коллинеарные |
|
|
|
|
a || b |
|
векторы |
|
|
|
|
|
|
|
|
|
|
|
|
|
124 |
Раздел 2. Векторы и координаты |
|
|||
|
|
Таблица 17 (продолжение) |
|||
|
Понятие |
Геометрическая |
Символическая |
|
|
|
иллюстрация |
запись |
|||
|
|
||||
|
Одинаково |
|
|
|
|
|
направленные |
|
a ↑↑ b |
||
|
векторы |
|
|
|
|
|
Противо- |
|
|
|
|
|
положно |
|
a ↑↓ b |
||
|
направленные |
|
|||
|
векторы |
|
|
|
|
|
Сумма векторов |
|
c = a + b |
||
Разность |
c = a − b |
векторов |
Произведение |
|
b |
= λa, λ > 0 |
|
|||||||||
вектора на |
|
|
|||||||||||
число |
|
b |
= λa, λ < 0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скалярное |
|
a b = |
|
a |
|
|
|
b |
|
|
|
||
произведение |
|
|
|
|
|
|
cos α |
||||||
|
|
|
|
||||||||||
|
|
||||||||||||
векторов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Разложение |
|
m = ma + mb + mc |
|||||||||||
|
|||||||||||||
вектора на |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
составляющие |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Готовимся к тематическому оцениванию по теме |
|
|
|
|
|
|
|
|
|
|
|
|
|
125 |
|
|
||||||||||||
|
Действия над векторами в координатной форме |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 18 |
||||||||
|
Векторы, результат |
|
|
|
|
|
Координаты вектора, |
|
|
|
|
|
||||||||||||||||
|
действия над ними |
|
|
результат действия над ними |
|
|||||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x1; y1; z1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x2; y2; z2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
a +b |
|
|
|
|
|
|
|
|
(x1 + x2; y1 + y2; z1 + z2) |
|
|
|
|
|
|
||||||||||||
|
a −b |
|
|
|
|
|
|
|
|
(x1 – x2; y1 – y2; z1 – z2) |
|
|
|
|
|
|
||||||||||||
|
λa |
|
|
|
|
|
|
|
|
|
|
|
|
|
(lx1; ly1; lz1) |
|
|
|
|
|
|
|
|
|||||
|
a b |
|
|
|
|
|
|
|
|
|
|
x1x2 + y1y2 + z1z2 |
|
|
|
|
|
|
|
|
||||||||
|
Основные формулы метода координат |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 19 |
||||||||
|
Величина |
|
|
|
|
|
Формула для вычисления |
|
||||||||||||||||||||
|
Длина вектора a |
|
|
|
|
|
|
|
|
|
a = (x, y, z) |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
= |
x2 + y2 + z2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Длина отрезка М1М2 |
|
|
|
|
|
|
M1 (x1 ; y1 ; z1 ), M2 (x2 ; y2 ; z2 ) |
|
|
|
|
||||||||||||||||
|
|
M |
M |
2 |
= |
(x |
2 |
− x )2 |
+ ( y − y )2 |
+ (z |
2 |
− z )2 |
|
|||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
2 |
|
|
1 |
|
|
|
1 |
|
|
||||
|
Угол j между |
|
|
|
|
|
|
a = (x , |
y , z ), b = (x , y , z ) |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
1 |
|
2 |
|
2 |
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
векторами a и b |
|
|
|
|
|
cos ϕ = |
|
|
|
|
|
x1x2 + y1 y2 + z1z2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x2 |
+ y2 |
+ z2 x |
2 + y2 |
+ z2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 |
|
2 |
|
2 |
|
|
2 |
|
|
|
||
|
Свойства векторов в координатной форме |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 20 |
||||||||
|
Свойство |
Коллинеарность |
|
|
Перпендикулярность |
|
||||||||||||||||||||||
|
векторов a и b |
|
|
|
|
векторов a и b |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Представление |
|
a = (x1; y1; z1), |
|
|
|
|
|
a = (x1; y1; z1), |
|
|
|||||||||||||||||
|
свойства в коорди- |
|
b = (x2; y2; z2) ≠ 0 |
|
|
|
|
|
b = (x2; y2; z2) |
|
|
|
|
|||||||||||||||
|
натной форме |
|
|
x1= lx2, |
|
|
|
|
|
|
x1x2 + y1y2 + z1z2 = 0 |
|
|
|||||||||||||||
|
|
|
|
y1 |
= ly2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
z1 |
= lz2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

Исторический комментарий
Идея изображения величин отрезками (не направленными) ис- пользовалась в Древней Греции. В физике, начиная с XVI ст., уче- ные с помощью направленных отрезков изображали действие сил
(Леонардо да Винчи (1452–1519), Г. Галилей (1564–1642) и др.).
Голландский математик и инженер С. Стевин (1548–1620) разлагал силы на составляющие и ввел правило параллелограмма.
Вматематикупонятиевекторавошлозначительнопозже.Первым векторное исчисление предложил норвежский математик К.Вессель (1745–1818), хотя его работы остались вне поля зрения современ- ников. Поэтому творцами векторной алгебры считают английско- го математика В. Гaмильтoна (1805–1865), немецкого математика Г. Грассмана (1809–1887). Современный вид векторное исчисление приобрело в конце XIX ст. в трудах американского физика и мате- матика Дж. Гиббса (1839–1903) и aнглийcкoro физика О. Xeвиcaйдa (1850–1925). С конца ХІХ века векторная алгебра и векторный ана- лиз стали надежным инструментом математиков и физиков.
Введение в математику координатного метода связывают с французскими математиками Р. Декартом (1596–1650) и П. Фер- ма (1601–1665). И хотя исторически первым к идее характеризо- вать точки плоскости с помощью пар чисел – координат – пришел П. Ферма, первым опубликовал и активно пропагандировал ко- ординатный метод именно Р. Декарт. Ему и отдают первенство открывателя аналитической геометрии. Р. Декарт четко сформу- лировал идею моделирования геометрических образов алгебраи- ческими средствами и с помощью своего метода дал решение не- скольких классических задач геометрии.
Как ни странно, координатный метод в пространстве стали при- менять лишь через сто лет. Первым, кто постоянно и широко исполь- зовал координаты в стереометрии, был французский математик А. Клеро (1713 – 1765). Швейцарский математик Л. Эйлер (1707 – 1783), долгое время работавший в Петербурге, составил близкий к современному курс аналитической геометрии пространства.

ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ
Ранее рассматривались элементарные методы исследования функций — математических моделей многих реальных процессов и явлений. В этом разделе мы познакомимся с новыми методами исследования функций — методами дифференциального исчисления. Методы дифференциального исчисления дают возможность сводить изучение сложного процесса к более простому — равномерному, находить его скорость и ускорение, определять условия оптимального протекания процесса, оце-
нивать допущенные погрешности, строить графики и т. п. Особое внимание в данном разделе будем уделять закреплению и развитию навыков «чтения» и построения графиков функций. Использование производной позволит точнее изображать графики функций. Будем решать прикладные задачи, в частности, на нахождение наибольшего и наименьшего значений функций. Производную будем использовать для исследования и решения уравнений и неравенств.
Готовимся к изучению темы «Производная и ее приложения»
Изучение темы «Производная и ее приложения» целесообразно начать с обзора основных классов функций, изучавшихся ранее, их свойств и графиков, общих свойств функций, построения и чте- ния их графиков. Для подготовки к изучению темы важнейший материал приведен в виде таблиц.
Линейная функция
|
|
|
|
|
|
|
|
|
Таблица 21 |
Функция |
|
|
|
График |
|
|
|
Свойства |
|
у = kx + b, k > 0 |
|
|
k>0 |
y |
|
|
|
|
D(y)= R; E(y)= R; |
k — тангенс угла |
j |
|
|
|
y=kx+b |
|
|
|
возрастающая, |
наклона ее графика |
|
|
|
|
|
|
|
непрерывная, имеет |
|
(прямой) к оси х; |
|
|
|
b |
|
|
|
|
нуль x = − b |
b = y(0) |
|
|
|
b |
O |
x |
|||
|
|
|
k |
||||||
|
|
|
|
|
|
|
|||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = kx + b, k < 0 |
|
|
k<0 |
y |
|
|
|
|
D(y)= R; E(y)= R; |
|
|
|
y=kx+b |
|
|
|
|
убывающая, |
|
|
|
|
|
|
|
|
|
|
непрерывная, имеет |
|
|
|
|
|
|
|
|
нуль: x = − b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||
|
|
|
|
b |
O |
k |
|||
|
|
|
|
|
|
|
|||
|
|
|
|
k b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = b |
|
|
k=0 |
y |
|
|
|
|
D(y)= R; E(y)= {b}; |
|
|
|
y=b |
|
|
|
|
|
постоянная, |
|
|
|
|
b |
|
|
|
непрерывная |
|
|
|
|
|
|
|
|
x |
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
O |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Готовимся к изучению темы «Производная и ее приложения» |
129 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Монотонность функции |
|
|
|
Таблица 22 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Возрастающая функция |
|
|
Убывающая функция |
|
||||||||||||||||||||||||||||||||||
|
|
x2 > x1 f(x2) > f(x1) |
|
|
|
|
|
x2 > x1 f(x2) < f(x1) |
|
|||||||||||||||||||||||||||||||
|
|
(большему значению аргумента |
|
(большему значению аргумента |
|
|||||||||||||||||||||||||||||||||||
|
|
из области определения функ- |
|
из области определения функ- |
|
|||||||||||||||||||||||||||||||||||
|
|
ции соответствует большее зна- |
|
ции соответствует меньшее зна- |
|
|||||||||||||||||||||||||||||||||||
|
|
чение функции). |
|
|
|
|
|
|
чение функции). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
y |
|
|
y=f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
y |
f(x1) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
f(x2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
f(x1) |
|
|
|
|
|
|
|
f(x2) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x1 O |
|
|
|
x2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 O |
|
|
|
|
|
|
|
|
x2 x |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нули и промежутки знакопостоянства функции |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 23 |
||||||||
|
Нули функции — абсциссы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
точек |
|
пересечения |
графика |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
функции с осью х. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Промежутки знакопо сто |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
янства функции |
|
— |
проме- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
жутки, |
|
где функция |
|
|
прини- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
x1, x2, x3 — нули функции |
|
||||||||||||||||||||||||||||||||||
|
мает |
|
положительные |
или |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
f(x) > 0 x [a; x1) (x2; x3) |
|
|||||||||||||||||||||||||||||||||||
|
отрицательные |
|
|
значения. |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
f(x) < 0 x (x1; x2) (x3; b] |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
Построение графиков функций |
|
|
|
Таблица 24 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
График функции у = f(x) + аполучают |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
из графика функции у = f(x) парал- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y=f(x)+a (a>0) |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
лельным переносом вдоль оси |
у на |
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
y=f(x) |
|
|||||||||||||||||
|
|
|а| единиц: в направлении оси у, |
|
если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||
|
|
а>0,ивнаправлении,противополож- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
ном направлению осиу, если а < |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y=f(x)+a (a<0) |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
График функции у = f(x + b) получа- |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
y=f(x) |
|
||||||||||||||||||||||
|
|
ют из графика функции у = f(x) па- |
|
|
|
|
|
y=f(x+b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
раллельным переносом вдоль оси х |
|
|
|
|
|
(b>0) |
|
|
|
|
|
|
|
y=f(x+b) |
|
|||||||||||||||||||||||
|
|
на |b| единиц: в направлении оси х, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b<0) |
|
||||||||||||||||||
|
|
если b |
< 0, и в направлении, проти- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
воположном оси |
х, если b > 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
Тест для диагностики |
|
||||||
|
|
|
|
|
|
готовности к изучению |
|
||||||
|
|
|
|
|
|
темы «Производная и ее |
|
||||||
|
|
|
|
|
|
приложения» |
|
|
|
|
|||
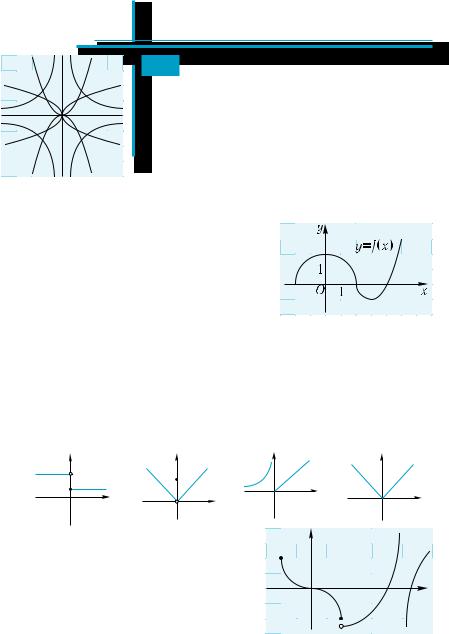
1. На рисунке изображен график фун- |
|
|
|
|
|
||||||||
|
кции у = f(x). |
|
|
|
|
|
|
|
|
|
|||
|
1) Сколько нулей имеет функция? |
|
|
|
|
|
|||||||
|
А. 0. |
|
|
|
Б. |
1. |
|
|
|
|
|
|
|
|
В. 2. |
|
|
|
Г. |
3. |
|
|
|
|
|
|
|
|
2) Определите знак числаа = f(2) – f(3). |
|
|
|
|
|
|||||||
|
А. а |
< 0. |
|
Б. а = 0. |
|
|
|
|
|
|
|
||
|
В. а |
> 0. |
|
Г. |
Определить невозможно. |
|
|
|
|
||||
|
3) Укажите наибольший из промежутков убывания функции. |
||||||||||||
|
А. [–2; 2]. |
|
Б. |
[0; 2]. |
В. |
[0; 3]. |
|
Г. [–2; 0]. |
|
||||
|
4) Укажите наибольшее и наименьшее значения функции. |
|
|||||||||||
|
А. f(0), f(3). |
|
Б. f(5), f(3). |
В. f(5), f(–2). |
Г. f(3), f(5). |
|
|||||||
2. На каком рисунке изображен график функции, непрерывной |
|||||||||||||
|
в своей |
|
определения? |
|
|
|
|
|
|
||||
|
А. |
|
|
|
Б. |
y |
В. |
y |
|
Г. |
y |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x |
|
|
|
O |
|
x |
O |
x |
|
|
|
|
|
|
O |
x |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
3. |
На рисунке изображен график фун- |
y |
|
y=f(x) |
|
||||||||
|
кции у = f(x). |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
|
|
|
||||
|
1) Укажите все ее точки разрыва. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
А. х = 3. |
|
|
|
|
|
|
|
|
|
|
||
|
Б. х1 |
= 1, х2 |
= 3. |
|
|
|
O |
1 |
2 |
3 |
x |
||
|
|
|
|
|
|
|
|
|
|||||
|
В. х1 |
= |
0, х2 |
= 1, х3 = 3. |
3. |
|
|
|
|
|
|
||
|
Г. х1 |
= |
–1, х2 = |
0, х3 = 1, х4 = |
|
|
|
|
|
|
|||
|
2) В какой из точек разрыва эта функция определена? |
|
|||||||||||
|
А. Функция не определена ни в одной из точек разрыва. |
|
|||||||||||
|
Б. х = 3. |
|
|
В. х = |
1. |
|
Г. х1 = 3, |
х2 = |
1. |
|
|||
