978-966-10-2413-6_Matematuka 11_rus

99 Kонтрольные вопросы

1°. Находятся ли точки A(2; –1; 3) и B(3; –2; 1) на одинаковом рас- стоянии от начала координат?

2°. Перпендикулярны ли векторы a = (1; 2; 3) и b = (1; –2; 1)?

3°. Коллинеарны ли векторы a = (2; 1; 1) и b = (–4; –2; 2)?

4. Перпендикулярны ли прямые AB и AC, если A(2; 1; 3),

В(0; 1; –1), C(–2; 0; 3)?

5. Параллельны ли прямые AB и CD, если A(2; 1; 3), B(1; 0; 2),

C(1; –2; 2), D(0; –1; –1)?

6. Симметричны ли точки А(2; –1; 2) и В(4; 3; 2) относительно точки М(3; 1; 2)?

7. Какой геометрический смысл имеют числа a i , a j , a k ?

4. Уравнения фигур

Из планиметрии известно, что фигуры на коор-

динатной плоскости, в частности линии, можно зaдaвaть уравнениями с двумя переменными.

Haпpимер, уравнение пpямoй имеет вид ax + bу + c = 0, а окруж- ность с центром в точке О(а; b) и радиусом R может быть задана уравнением (x – a)2 + (y – b)2 = R2.

В пространстве точка характеризуется тремя координатами. Уравнение с тремя переменными определяет определенную фи-

гуру в пространстве, координаты точек которой удовлетворяют данному уравнению, а координаты других точек пространства не удовлетворяют ему. Рассмотрим уравнение

x2 + y2 + z2 = R2 .

Это уравнение похоже на уравнение окружности и поэтому естественно надеять- ся, что оно описывает аналог окружности в

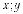
пространстве — сферу (рис. 61). Действи-

тельно, выражение, расположенное в левой части уравнения, имеет простой геометри- ческий смысл — квадрат расстояния от точ- ки C(x; у; z) до начала координат О(0; 0; 0). Taким образом, уравнение описывает сово- купность всех точек пространства, квадрат

расстояния которых от начала координат одинаков и равен R2.

Фигура, составленная из всех точек npocmранства, расстояния от которых до заданной moчкu одинако- вы, нaзывaеmся сферой.

Заданная точка называется центром сферы. Расстояние R от точек сферы до ее центра называется радиусом cфepы.

Уравнение x2 + y2 + z2 = R2 , R > 0, определяет сферу с центром

в начале координат и радиуса R. Heтруднo составить уравнение сферы радиуса R и с центром в точке (а; b; c). Для этого нужно записать квадрат расстояния от произвольной точки сферы (x; у; z) до центра (а; b; c) и приравнять его R2:

(x − a)2 + (y − b)2 + (z − c)2 = R2 .

Линейному уравнению ах + bу + c = 0 на плоскости соответству- ет в пространстве уравнение

ах + by + cz + d = 0.

Можно предвидеть, что это уравнение определяет плоскость, если не все коэффициенты при его переменных равны нулю од- новременно. Аргумeнтировать этот вывод можно по-разному. На- пpимер,частныеслучаиприведенногоуравнения x = m,y = n,z = h

определяют плоскости, параллельные координатным плоскостям. Пересечению такой плоскости, например z = h, с фигурой, задан- ной уравнением ах + by + cz + d = 0, соответствует в этой плоскости

уравнение ах + bу + ch + d = 0, то есть уравнение прямой (кроме случая, когда а = b = 0).

Пользуясь уравнениями фигур в пространстве, можно решать многочисленные задачи, связанные с этими фигурами, в частно- сти исследовать их взаимное расположение.

тельно плоскости xz.

 1) Точка лежит на данной сфере тогда и только тогда, когда

ее координаты удовлетворяют уравнению сферы. Подставив коор- динаты точки в уравнение сферы, будем иметь: (–1 – 3)2 + (2 + 1)2 + + 02 = 25. Получили верное числовое равенство: (–4)2 + 32 = 25. Сле- довательно, данная точка принадлежит сфере.

2) Центром сферы является точка с координатами (3; –1; 0). Найдем расстояние d между точками с координатами (0; 2; –1) и (3; –1; 0) по формуле для нахождения расстояния между двумя точками, заданными координатами:

d = (3 − 0)2 + (−1 − 2)2 + (0 + 1)2 = 9 + 9 + 1 = 19 .

3)Радиус данной сферы равен 5. Сфера радиуса 5 и с центром

вточке (0; 2; –1) имеет уравнение

х2 + (у – 2)2 + (z + 1)2 = 25.

4)Сфера, симметричная данной относительно плоскости хz, имеет тот же радиус. Ее центр симметричен центру (3; –1; 0) дан- ной сферы относительно плоскости хz. Поэтому он имеет коорди- наты (3; 1; 0). Искомое уравнение имеет вид:

(x − 3)2 + ( y −1)2 + z2 = 25. g

Пример 8. Даны плоскость 3х + 4у + z = 1 и точка А(1; – 1; 2). 1) Лежит ли точка А в данной плоскости?

2) Найти точки пересечения данной плоскости с координатными осями.

 1) Подставим координаты точки А в уравнение плоскости: 3 1 + 4 (–1) + 2 = 1. Получили верное равенство 3 – 4 + 2 = 1. Точка А лежит в данной плоскости.

2) Ординаты и аппликаты точек координатной оси х равны нулю. Поэтому абсцисса точки пересечения данной плоскости с

осью х удовлетворяет уравнению 3 х + 4 0 + 0 = 1, или х = 13 . Иско-

Если хотя бы один из параметров а, b, с не равняется нулю, то нетрудно найти такую точку М0(х0; у0; z0), что

ax0 + by0 + cz0 + d = 0.

Вычитая это равенство из уравнения ах + by + cz + d = 0, полу- чим уравнение, равносильное данному:

a (x − x0 ) + b(y − y0 ) + c (z − z0 ) = 0 .

Полученное соотношение можно интерпретировать на «вектор-

ном» языке. Пусть n = (a;b;c) , а M0 M = (x − x0 ; y − y0 ; z − z0 ), где M — точка с координатами (х; у; z). Тогда это уравнение можно записать с помощью скалярного умножения:

M M 0 . n 0 =

Совокупность всех точек M, удовлетворяющих этому условию, образует плоскость, проходящую через точку (х0; y0; z0) перпенди- кулярновектору n . Beктоp n называютнopмaльнымвeкmopoм nлoскости. Его координатами являются коэффициенты при пе- ременных.

Действительно, точка с координатами (х0; y0; z0) удовлетворяет этому условию, так как n 0 = 0 .

множество всех точек пространства, удаленных от начала коорди- нат не более чем на R, то есть шар.

Hepавенство z ≥ h определяет полупpocтранство.

5.Какие из данных уравнений определяют плоскость в про- странстве:

а°) х = –1; б°) х – 2у + z = 0; в) х – у + 1 = 0?

Графические упражнения

1.Постройте изображение точек по их координатам:

а) А(3; 1; 2): б) В(0; –1; 3); в) С(–2; 1; 3); г) D(12;

Куб ABCDA1B1C1D1 с ребром 2 расположен в прямоугольной системе координат так, как это показано на рис. 63, а)–г). Ука- жите координаты вершин куба.

Правильный тетраэдр SABC с ребром 3 расположен в прямо- угольной системе координат так, как это показано на рис. 64, где начало координат О является центром грани АВС.

а) Укажите координаты точки О.

б) Укажите координаты вершин тетраэдра.

4.Тетраэдр SABC расположен в прямоугольной системе коорди- нат так, как это показано на рис. 65. Треугольник АВС – рав- нобедренный прямоугольный с гипотенузой АВ = с, SO = h. Укажите координаты вершин тетраэдра.

5.Тетраэдр SABC расположен в прямоугольной системе коорди- нат так, как это показано на рис. 66. Треугольник АВС – пра- вильный со стороной а, SB ^ ABC, SB = l. Укажите координа- ты вершин тетраэдра.

Задачи

98.Дана точка (–3; 1; 2). Найдите:

1°) координаты ее проекций на координатные оси;

2)координаты ее проекций на координатные плоскости;

3)расстояния от данной точки до координатных плоскостей.

99.Куб ABCDA1B1C1D1 расположен в прямоугольной системе ко- ординат с началом в точке D и осями x, у, z, направленными соответственно вдоль ребер DA, DC, DD1. Длина ребра куба равна 1.

1)Найдите координаты вершин B, C, C1.

2)Найдите координаты середины ребра CC1.

3)Какая из вершин куба наиболее удалена от точки (1; 1; 1)?

109.Даны четыре вершины A(3; 0; 2), B(2; 4; 5), A1(5; 3; 1),

D1(7; 1; 2) параллелепипеда ABCDA1B1C1D1. Найдите коор- динаты вершины: l) D; 2) B1; 3) C1.

110.Даны точки А(4; 0; –3), В(8; 0; 1), С(2; 0; –1), D(–2; 0; 3).

1°) Найдите длину вектора CD и угол, образованный им с осью х.

2°) Перпендикулярны ли векторы AB и CD ? 3°) Коллинеарны ли векторы AC и CD ?

4)На оси абсцисс найдите точку, равноудаленную от точекВи С.

5)Найдите координаты вектора, противоположно направ-

ленного с вектором CD и имеющего длину 2.

6) Найдите такую точку N, чтобы четырехугольник ABND был параллелограммом.

111. Даны точки А(–2; 2; 0), В(0; 1; 1), С(4; 2 ;0), D(1; 1; 0).

1°) Найдите длину вектора CA и угол, образованный им с осью х.

2°) Перпендикулярны ли векторы DB и DC ?

3°) Коллинеарны ли векторы AC и BD ?

4) На оси ординат найдите точку, равноудаленную от точек

А и С.

5) Найдите координаты вектора, противоположно направ-

ленного с вектором AC и имеющего длину 3.

6) Найдите такую точку М, чтобы четырехугольник ABСМ был параллелограммом.

112. Даны векторы a = (3; –1; 0), b =(2; 2; 1), c = (–3; 0; 4).

1) Найдите векторы, коллинеарные вектору a и длины ко- торых втрое больше длины вектора a .

2) Найдите хотя бы один вектор, перпендикулярный векто- ру c .

3) При каком значении p векторы a и d = (1; p; 2) перпенди- кулярны?

4) При каком значении p векторы b и m = (p; –2; –1) колли- неарны?

113. Даны точки:

1) А(–3; 1), B(1; 3), C(2; 1), D(–2; –1);

2) А(–1; 2; 4), B(1; 0; 2), C(2; –3; 0), D(0; –1; 2).

Определите тип четырехугольника ABCD.

114. Докажите, что точки А(1; –1; 1), B(1; 3; 1), C(4; 3; 1), D(4; –1; 1)

являются вершинами прямоугольника. Вычислите длины его диагоналей и координаты точки их пересечения.

115. Дана сфера (х + 3)2 + у2 + (z – 1)2 = 16. 1°) Лежит ли на сфере точка (–3; 1; 5)?

2°) Найдите расстояние от центра сферы до точки (–5; 2; 0). 3°) Составьте уравнение сферы того же радиуса и с центром в точке (–5; 2; 0).

4) Составьте уравнение сферы, симметричной данной отно- сительно плоскости yz.

116. Дана сфера х2 + (у + 2)2 + (z – 3)2 = 16. 1°) Лежит ли на сфере точка (0; –2; 7)?

2°) Найдите расстояние от центра сферы до точки (1; 0; –2). 3°) Составьте уравнение сферы с тем же центром и с диаме- тром 6.

4) Составьте уравнение сферы, симметричной данной отно- сительно плоскости xy.

117. Даны точки А(1; –1; 2), В(2; 3; –5), С(–1; 3; –2) и плоскость a,

заданная уравнением 3x + 4y – z = 1. 1°) Лежит ли точка А в плоскости a?

2°) Найдите точки пересечения плоскости a с координатны- ми осями.

3°) Составьте уравнение плоскости b, проходящей через точ- ку В перпендикулярно прямой АС.

4) Определите взаимное расположение плоскостей a и b.

5) Найдите угол между плоскостями a и b.

118. Имеем точки А(2; –1; 3), В(1; 0; –1), С(–1;2;1) и плоскость a,

заданную уравнением x – 2y + 3z = 2. 1°) Лежит ли точка С в плоскости a?

2°) Найдите точки пересечения плоскости a с координатны- ми осями.

3°) Составьте уравнение плоскости b, проходящей через точ- ку А перпендикулярно прямой ВС.

4) Определите взаимное расположение плоскостей a и b.

5) Найдите угол между плоскостями a и b.

119. Докажите, что плоскость, пересекающая координатные оси в точках (а; 0; 0), (0; b; 0) и (0; 0; с), abc ≠ 0, имеет уравнение

ax + by + zc = 1 .