
978-966-10-2413-6_Matematuka 11_rus
.pdf
О.Н. Афанасьева Я.С. Бродский А.Л. Павлов А.К. Слипенко
МАТЕМАТИКА
класc
Учебник для общеобразовательных
учебных заведений
Уровень стандарта
Рекомендовано Министерством образования и науки Украины
ТЕРНОПОЛЬ НАВЧАЛЬНА КНИГА — БОГДАН 2011
ББК 22.1я72 А94
Рекомендовано Министерством образования и науки Украины (приказ МОН Украины №235 от 16.03.2011 г.)
Издано за счет государственных средств. Продажа запрещена. Научную экспертизу проводил Институт математики НАН Украины. Психолого-педагогическую экспертизу проводил Институт педагогики НАПН Украины.
Афанасьева О.Н., Бродский Я.С., Павлов А.Л., Слипенко А.К.
А94 Математика. 11 класс. Уровень стандарта: Учебник для обще образоват. учеб. зав. — Тернополь: Навчальна книга – Богдан, 2011. — 480 с.
ISBN 978-966-10-2413-6
Предлагаемый учебник соответствует программе по математике для 11-го класса уровня стандарта и направлен на подготовку учащихся к широкому и сознательному применению математики. Эту ориентацию обеспечивают содержание курса, характер изложения учебного материа- ла, отбор иллюстраций и примеры приложений, система упражнений и контрольных вопросов.
Для учащихся и учителей общеобразовательных учебных заведе- ний.
ББК 22.1я72
Охраняется законом об авторском праве.
Ни одна часть этого издания не может быть воспроизведена в любом виде без разрешения автора или издательства
|
© |
Афанасьева О.Н., Бродский Я.С., |
|
|
Павлов А.Л., Слипенко А.К., 2011 |
ISBN 978-966-10 |
© Навчальна книга – Богдан, макет, |
|
|
художественное оформление, 2011 |
|

! Обращение к читателю
Дорогой юный друг!
Перед Вами учебник по предмету «Математика». Его главное назна- чение — помочь Вам систематизировать, расширить и углубить знания и умения, необходимые для математического моделирования и иссле- дования процессов и явлений с помощью функций, уравнений, про- изводной, интеграла, вероятности и других математических объектов, овладеть смежными предметами (физикой, химией, биологией и т. д.) и тем самым удостовериться в могуществе математических методов для познания окружающего мира и решения различных проблем.
Учебник для 11 класса состоит из семи разделов. Каждому разде- лу предшествует материал, изучавшийся ранее и необходимый для изучения этого раздела. Он представлен в виде таблиц. Для обеспе- чения готовности к изучению материала раздела приводится диаг- ностический тест.
Разделы учебника состоят из параграфов, которые, в свою очередь, делятся на пункты. К каждому пункту даны контрольные вопросы, целью которых является обеспечение активного усвоения основных понятий и фактов в их взаимосвязи.
Изложение учебного материала в каждом пункте структурирова- но по уровням. На первом уровне (он обозначен буквой Б) излагают- ся основные понятия и факты темы, хотя, чаще всего, без формаль- ных доказательств. Этот материал является базой для последующего изучения темы, более основательного и полного.
На втором уровне (он обозначен буквой О) приводится более полное обоснование предыдущего материала, его расширение, при- водятся примеры его применения. Материал на этих двух уровнях обеспечивает овладение предметом в соответствии с требованиями программы уровня стандарта.
Изложение теоретического материала сопровождается примера- ми и решениями типовых задач соответствующего уровня. Начало и конец доказательств утверждений и решений примеров и задач обо- значены знаками и .

4 |
Обращение к читателю |
Система задач, упражнений и контрольных вопросов, приведен- ных в учебнике, имеет три уровня сложности: первый уровень слож- ности обозначен символом «°», второй не имеет обозначений, третий обозначен символом «*».
В общую систему заданий включены упражнения на повторе- ние, которые должны способствовать обеспечению готовности к ов- ладению последующим материалом, сохранению умений и навыков, сформированных при изучении предыдущих разделов.
Каждый раздел завершается материалом для подготовки к тема- тическому оцениванию, состоящим из заданий для самоконтроля (с ответами) и образца тематической контрольной работы. Для повторе- ния и систематизации учебного материала раздела приведены соот- ветствующие таблицы. Каждый из разделов завершается историче- ским комментарием.
Учебник содержит указания и ответы к задачам, а также предмет- ный указатель.
Чтение книги не является легким делом. Некоторые фрагменты доказательств оставлены для самостоятельной проработки. Не про- пускайте их!
Желаем успехов!
Коллектив авторов
Обозначения для ориентирования в учебном материале



 ,
, 

 — две ступеньки усвоения учебного материала
— две ступеньки усвоения учебного материала
!— обратите внимание
— начало решения задачи, доказательства теоремы — конец решения задачи, доказательства теоремы ° — задачи первого уровня сложности * — задачи третьего уровня сложности
— контрольные вопросы— графические упражнения; задачи
— исторический комментарий  — границы для различных типов задач— упражнения для повторения ? — задания для самоконтроля— тест для диагностики
— границы для различных типов задач— упражнения для повторения ? — задания для самоконтроля— тест для диагностики

ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
Основным назначением современной математики является моделирование явлений природы и общества. Понятие функции относится к важнейшим средствам моделирования. Поэтому вполне естественной и актуальной является проблема расширения классов изучаемых функций. В этом разделе мы познакомимся с новыми функциями, которые будут введены с помощью операции возведения в степень и операции, обратной к ней. Свойства и графики таких функций будем изучать с помощью методов, использовавшихся в курсе математики 10-го класса.
В естественных науках и технике встречаются процессы, рост или
«угасание» которых происходит быстрее, чем у любой степенной функции. Такие процессы описываются показательными функциями. Для их изучения необходимо воспользоваться еще одной (кроме извлечения корня) операцией, обратной возведению в степень. Она называется логарифмированием. Функции, вводимые с помощью этой операции, то есть логарифмические функции, также широко применяются для описания реальных процессов и явлений.

Готовимся к изучению темы «Показательная и логарифмическая функции»
Изучение темы «Показательная и логарифмическая функции» существенно использует материал темы «Функции, их свойства и графики», изучавшийся в 10 классе, и практически весь алге- браический материал из предыдущих классов (вычисления, вы- ражения и их преобразования, уравнения и неравенства, после- довательности). Для подготовки к изучению темы важнейший материал приведен в виде таблиц.
Определение степени с рациональными показателями
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 |
|
Степень с натуральным по- |
|
n N, n > 1 an = a a ... a. |
||||||||||||
казателем |
|
а1 = а. |
|
|
|
|
|
|
n а |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
Степень с нулевым показате- |
|
а0 = 1, а ≠ 0. |
|
|
|
|
|
|
|
|||||
лем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Степень с целым отрица- |
|
a |
−n |
= |
1 |
, a ≠ 0, |
n N . |
|
|
|||||
тельным показателем |
|
|
|
|
|
|
||||||||
|
|
a |
n |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Степень с рациональным по- |
|
|
m |
= n am , a > 0, n N, n > 1, m Z. |
||||||||||
казателем |
|
an |
||||||||||||
Свойства степени с рациональным показателем |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
|
Произведение степеней с одинаковыми |
a |
x |
a |
y |
= a |
x + y |
, x, y Q. |
|||||||
основаниями |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Частное от деления степеней с одинако- |
ax |
: ay = ax − y , x, y Q. |
||||||||||||
выми основаниями |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Возведение степени в степень |
|
|
|
|
|
|
(ax )y |
= axy , x, y Q . |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Готовимся к изучению темы «Показательная и логарифмическая функции» |
7 |
|
|||||
|
|
|
|
|
|
||
|
Степень произведения |
(ab)x |
= ax bx , x Q . |
|
|
||
|
Степень частного |
a x |
= |
ax |
|
|
|
|
|
b |
x , x Q . |
|
|
||
|
|
b |
|
|
|
|
|
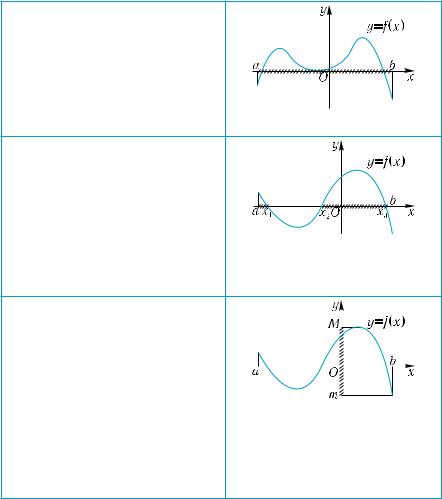
Чтение графика функции
Таблица 3
Область определения функции
D(f) = [a; b]
Нули функции, промежутки знакопостоянства функции
x1, x2, x3 — нули функции f(x) > 0 x [a; x1) (x2; x3) f(x) < 0 x (x1; x2) (x3; b]
|
|
|
|
|
|
Наибольшее, наименьшее зна- |
|
|
|
||
чения, множество |
значений |
|
|
|
|
функции |
M — наибольшее |
значение |
|||
|
функции |
значение |
|||
|
m — наименьшее |
||||
|
функции |
|
|
||
|
E( f ) = [m; M] |
|
|
||
8 |
Раздел 1. Показательная и логарифмическая функции |
||
|
|
|
|
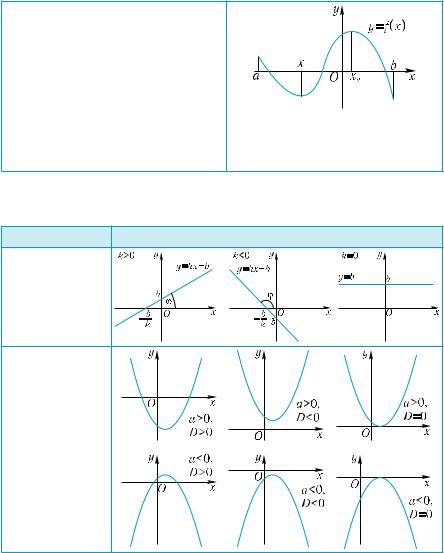
Промежутки монотонности функции
f (x) x [x1 ,x2 ]
f (x) x [a,x1 ],x [x2 ,b]
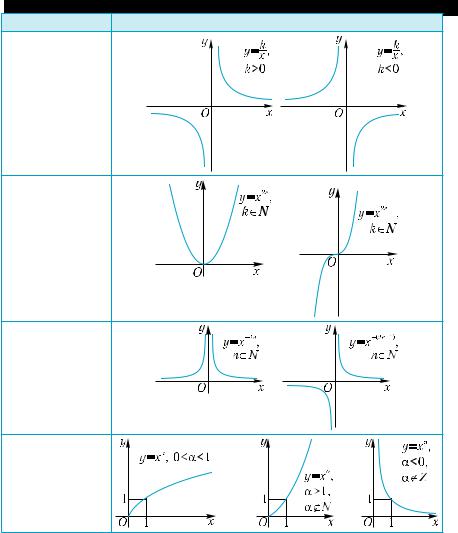
Основные классы функций
Таблица 4
Функции Графики
Линейная
функция
Квадратичная
функция
у = ах2 + bх + с
D = b2 – 4ac
Готовимся к изучению темы «Показательная и логарифмическая функции» |
9 |
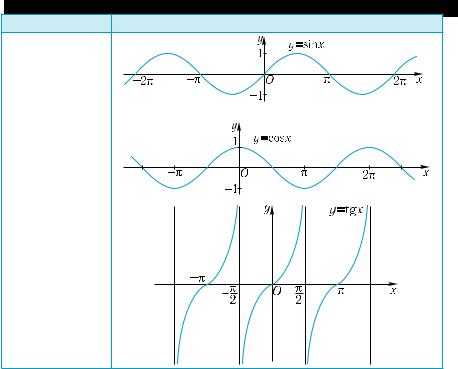
Функции Графики
Обратная пропорцио- нальность
Степенные
функции с натуральными
показателями
Степенные
функции с целыми от-
рицательными
показателями
Степенные
функции с дробными
показателями
10 |
Раздел 1. Показательная и логарифмическая функции |
Функции Графики
Тригонометрические функции
