
978-966-10-2413-6_Matematuka 11_rus
.pdf
Исследование функций и построение их графиков с помощью производной |
181 |
3. Корни уравнения x3 + 3x = а — это абсциссы точек пересече-
ния графика функции y = x3 + 3x и прямой у = а. Из рис. 109 и 110
видим, что прямая у =а пересекает график функции в единствен- ной точке лишь при a = ±4. Итак, при a = ±4 уравнение имеет единственный корень. g
99 Контрольные вопросы
1°. На рис. 111, а)–б) изображены графи-  кифункцийу=f(x) иу=g(x).Укажите
кифункцийу=f(x) иу=g(x).Укажите
свойства, общие для этих функций, и  свойства, которыми они отличаются.
свойства, которыми они отличаются. 
2. Известно, что f ′(x)= 2x – 1. Какой из 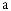
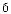 графиков функций, изображенных
графиков функций, изображенных 

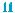
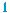 на рис. 112, а)–в), является графиком функции у = f(x)?
на рис. 112, а)–в), является графиком функции у = f(x)?
3.Постройте график какой-либо функции, удовлетворяющей условиям:
а) f ′(x) < 0 при x < 0, f ′(x) > 0 при x > 0, f ′(0) = 0;
б) f ′(x) > 0 при x < 0, f ′(x) < 0 при x > 0, f ′(0) не существует;
в) f ′(x) < 0 при x ≠ 0; f ′(0) = 0.
4.Какой из графиков, изображенных на рис. 113, а)–д), являет- ся графиком функции: а) y = x3 − x ; б) y = x3 + x ?

182 |
Раздел 3. Производная и ее приложения |
4. Наибольшее и наименьшее значения функции
Решение многих практических задач сводится к установлению условий, при которых исследуемая величина достигает своего наибольшего или наи-
меньшего значения.
Например, какие размеры должен иметь ящик, чтобы при опре- деленном количестве материала, израсходованного на его изго- товление, объем ящика был наибольшим? Как из круглого бревна изготовить прямоугольную балку с наименьшими затратами мате- риала? На какой высоте над центром круглой площади нужно под- весить фонарь, чтобы освещение было наилучшим? Как выполнить определенную работу за кратчайший срок?
Подобные задачи решаются с помощью производной. В первую очередь уточним понятие наибольшего и наименьшего значений функции.
Пусть функция у = f(x) определена на некотором промежутке и х0 — точка из этого промежутка.
Значениефункцииу= f(х) вточкех0 называютнаиболь-
шим значением функции на промежутке, если оно не меньше любого другого значения функции на нем.
Следовательно, если f(x0) — наибольшее значение функции на некотором промежутке, то для всех х из этого промежутка выпол- няется неравенство f(x) ≤ f(x0).
Значение функции у = f(х) в точке х0 называют наи-
меньшим значением функции на промежутке, если оно не больше любого другого значения функции на нем.
Следовательно, если f(x0) — наименьшее  значение функции на некотором промежутке,
значение функции на некотором промежутке,  то для всех х из этого промежутка выполняет-
то для всех х из этого промежутка выполняет-
ся неравенство f(x) ≥ f(x0).
Например, наибольшее значение функции
 у = f(x), график которой изображен на рис. 114, на промежутке [–2; 4] равно f(1) = 3, а наи-
у = f(x), график которой изображен на рис. 114, на промежутке [–2; 4] равно f(1) = 3, а наи-
меньшее равняется f(–2) = 1.
!Обратите внимание на то, что при определении наи большего и наименьшего значений функции на проме жуткемысравнивалиих со всеми значениямифункции на этом промежутке. В то же время при определении
Исследование функций и построение их графиков с помощью производной |
183 |
точки экстремума мы сравнивали значение функции в точке экстремума только со значениями функции из некоторой окрестности этой точки.
Если непрерывная функция возрастает на некотором отрезке [а; b], то наибольшее значение она принимает в точке b, а наи- меньшее — в точке а (рис. 115, а). Если непрерывная функция убывает на некотором отрезке [а; b], то наибольшее значение она принимает в точке а, а наименьшее — в точке b (рис. 115, б).
Если непрерывная функция не является монотонной на отрезке, то наибольшее или наименьшее значение она принимает не обяза- тельно на его концах. Наибольшее значение функция принимает или в точке максимума, или на концах отрезка (рис. 116), а наи- меньшее — или в точке минимума, или на концах отрезка (рис. 117).
Чтобы найти наибольшее и наименьшее значения дифферен- цируемой функции на заданном отрезке, достаточно:
1)найти точки, в которых производная функции равна нулю;
2)выбрать из них те, которые принадлежат заданному отрезку;
3)вычислить значение функции в этих точках и на концах от- резка;
4)среди полученных значений выбрать наибольшее и наименьшее. Пример 8. Найти наибольшее и наименьшее значения функ-
ции f(x) = x3 + x2 + 4x + 2 на отрезке [–1; 2].

184 |
Раздел 3. Производная и ее приложения |
Найдем производную функции:f′(x) = 3x2 + 2x + 4. Полученный квадратный трехчлен везде принимает положительные значения, то есть f′(x) >0. Функция возрастает на промежутке [–1; 2]. Следова- тельно, f(–1) = –2 — ее наименьшее значение, аf(2) = 22 — наиболь- шее на отрезке [–1; 2].g
Ответ. 22 и –2.
Пример 9. Материальная точка движется прямолинейно по закону x = t3 – 12t + 10. Найти наибольшую и наименьшую координаты точки на промежутке времени [0; 4].
Найдем производную функции: х′(t)= 3t2 – 12. Нулями про- изводной функции являются точки t1 = –2 и t2 = 2. Однако лишь одна из них, t = 2, принадлежит отрезку [0; 4]. Вычислим значе- ние функции на концах отрезка и в точке t2 = 2: x(0) = 10, x(4) = 26, x(2) = –6. Наибольшая координата точки равна х(4) = 26, наимень- шая равна х(2) = –6. g
Ответ. 26 и –6.
При решении прикладных задач сначала перево- дят задачу на язык математики, то есть строят ее математическую модель. Как известно, математи-
ческое моделирование состоит из трех этапов:
1)выбор или построение математической модели для описания данной задачи;
2)исследование построенной модели, то есть решение матема- тической задачи;
3)содержательное толкование результатов исследования и установление соответствия полученного результата цели иссле- дования.
Внашем случае для построения математической модели пред- ложим такую последовательность действий.
1.По условию задачи выделить величину, которую следует оп- тимизировать.
2.Выбрать удобную переменную, которая может быть аргумен- том функции, описывающей исследуемую величину.
3.Найти аналитическое выражение для функции.
4.Из условия задачи найти промежуток, на котором исследует- ся полученная функция.
Исследование функций и построение их графиков с помощью производной |
185 |
Так завершается первый этап математического моделирования: данная задача сводится к нахождению наибольшего или наимень- шего значения функции на некотором промежутке. С помощью производной или другими средствами (используя возрастание или убывание функции или свойства квадратичной функции и т. п.) ре- шают полученную задачу. После этого выясняется, какое реальное содержание имеет результат, полученный в терминах функций.
Приведем примеры применения описанного метода.
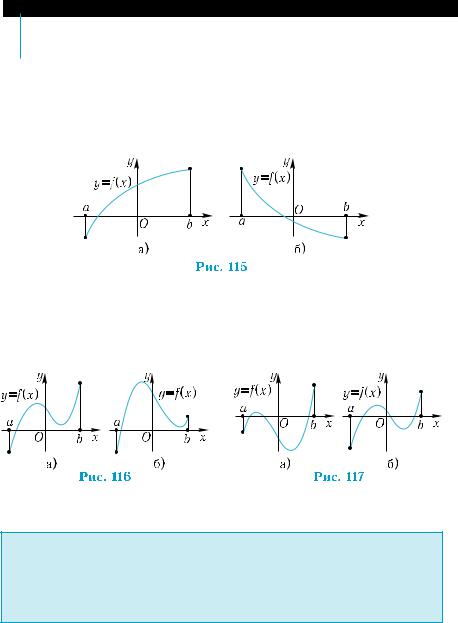
Пример 10. В отделе упаковки посылок принимают ящики, если сумма их длины и обхвата не превышает 150 см. Найти размеры ящика с двумя квадратными стенками, удовлетворяю- щего этому требованию и имеющему наибольший объем.
Математической мо- делью ящика для посылок (рис. 118, а) является пря- моугольный параллелепи-
пед (рис. 118, б). Оптимизи- ровать объем ящика — это значит выяснить, при ка-
ких значениях х и l, удов- летворяющих условию, объем параллелепипеда будет наибольшим. Как
известно, объем V прямоугольного параллелепипеда с квадрат- ной гранью равен: V = x2 l. По условию задачи, 4х + l = 150. Отсю- да l = 150 – 4x. Подставив полученное выражение для l в формулу для нахождения объема, получим функциональную зависимость:
V = x2(150 – 4x), где 0 < x < 1504 = 37,5 . Таким образом, необходимо
найти наибольшее значение функции V = 150x2 – 4x3 на интерва- ле (0; 37,5). Найдем по приведенной схеме наибольшее значение этой функции на отрезке [0; 37,5]. Производная исследуемой фун- кции равна: V ′ = 300x – 12x2. Производная принимает нулевое значение при х = 0 и х = 25. Поскольку V(0) = V(37,5) = 0, а V(25) = = 252 50 = 31250, то наибольшее значение на отрезке [0; 37,5], а поэтому и на интервале (0; 37,5) функция принимает при х = 25. Следовательно, оптимальные размеры ящика: (25×25×50) см. g
Ответ. (25×25×50) см.
186 |
|
Раздел 3. Производная и ее приложения |
|||||
Пример 11. Из трех одинаковых досок шириной а см нужно |
|
||||||
сделать желоб, поперечное сечение которого имело бы форму рав- |
|||||||
нобокой трапеции. Как это сделать так, чтобы пропускная спосо- |
|||||||
бность желоба была наибольшей? |
|
|
|
|
|
||
|
|
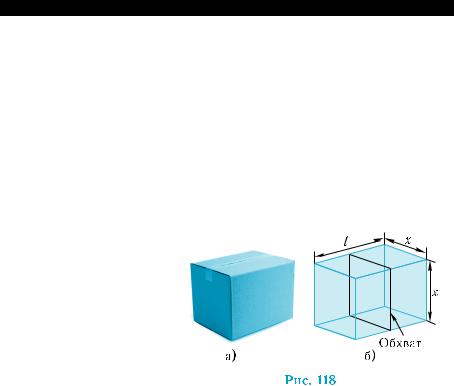
1. Построим математическую модель си- |
|||||
|
туации, рассматриваемой в задании. Про- |
||||||
|
пускная способность желоба будет наиболь- |
||||||
|
шей, если наибольшей будет площадь его |
||||||
|
поперечного сечения (рис. 119). Поэтому ве- |
||||||
|
личиной, которую необходимо оптимизиро- |
||||||
вать, является площадь трапеции |
ABCD. Представим площадь |
||||||
трапеции в виде функции некоторого аргумента. В качестве аргу- |
|||||||
мента выберем угол |
DAB при большем основании трапеции (по- |
||||||
нятно, что AB > a), обозначив его через x. Выразим площадь S |
|||||||
трапеции через x и известные величины. Так как DF = asin x, |
|||||||
AF = acos x, то S = |
AB + CD DF = |
a + a + 2a cos x asin x . |
Итак, |
||||
|
|
2 |
2 |
|
π |
|
|
|
|
|
|
0; |
|
||
S = a2(1+ cos x)sin x. Аргумент х меняется на промежутке |
2 |
. Та- |
|||||
|
|
|
|
|
|
||
ким образом, математической моделью данного задания является |
|||||||
задача: найти наибольшее значение функции S = a2(1 + cos x)sin x
|
|
|
|
|
|
|
|
|
|
|
π |
|
Найдем наибольшее значение функции |
|||||||
на промежутке 0; |
|
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
S = S(х) на отрезке |
|
|
π |
|
|
|
|
|
|
|||||||||||
0; |
2 |
. |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2x) = |
||||
2. Производная этой функции равна: S′= a2(cosx + |
||||||||||||||||||||
= 2a2cos |
3x |
|
cos x . Решив уравнение 2a2cos |
3x |
cos x = 0, устано- |
|||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
2 |
2 |
|
|
|
|||
вим, |
что на отрезке |
|
|
π |
|
|
|
|
|
|||||||||||
0; |
производная функции только в одной |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
точке x = |
|
|
p |
|
|
|
|
|
|
|
|
|
|
π |
= |
a2, |
||||
|
3 |
равняется нулю. Так как S(0) = 0, S |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
π |
|
|
|
2 |
|
3 3 |
|
|
2 |
, то наибольшего значения на отрезке |
|
π |
||||||||
S |
|
= a |
|
|
|
|
|
> a |
|
0; |
|
|||||||||
|
4 |
|
|
|||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||
функция |
|
S = |
|
S(х) |
|
достигает при х = p. |
Значение |
функции |
||||||||||||
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
S |
|
будет наибольшим и на интервале 0; |
2 |
. |
|
|
|
|||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Исследование функций и построение их графиков с помощью производной |
187 |
3. Таким образом, доски нужно соединить друг с другом под углом 120°. g
Ответ. Соединить доски под углом 120°.
99 Контрольные вопросы
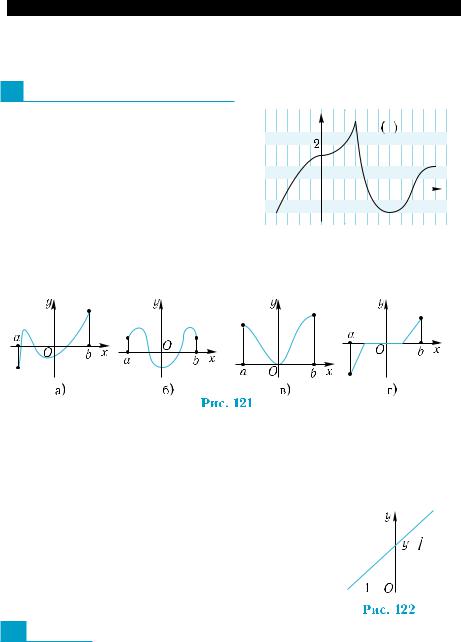
1°. На рис. 120 изображен график  функции у = f(x). Укажите наи-
функции у = f(x). Укажите наи- 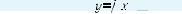 большее и наименьшее значения
большее и наименьшее значения  функции на отрезке [–2; 2].
функции на отрезке [–2; 2].  2°. Обязательно ли наибольшее зна-
2°. Обязательно ли наибольшее зна-  чение функция принимает в точ-
чение функция принимает в точ-  ке максимума?
ке максимума? 
3°. Среди функций, графики кото- 
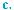

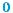 рых изображены на рис. 121, а)–г), укажите ту, которая наи-
рых изображены на рис. 121, а)–г), укажите ту, которая наи-
меньшее значение принимает в точке минимума, а наиболь- шее — на одном из концов отрезка [a; b].
4.Известно, что f ′(x) < 0 на промежутке [–1; 2]. В какой точке промежутка функция принимает наибольшее значение?
5.Производная функции у = f(x) имеет вид f ′(x) = x(x + 2). В ка- ких точках следует вычислить значения функции у = f(x), что- бы найти ее наибольшее и наименьшее значения на проме-
жутке [–3; –1]?
6.Существует ли функция, у которой наиболь- шее и наименьшее значения совпадают? 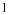


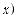 График производной функции у = f(x) изо-
График производной функции у = f(x) изо-
бражен на рис. 122. В какой точке функция  (x) принимает наименьшее значение?
(x) принимает наименьшее значение? 

Задачи
157.Докажите, что функция y = f (x) возрастает в своей области оп- ределения, если: 1°) f (x) = x3 + 2x + 1; 2) f (x) = 1 + 2x + sin x .
188 |
|
|
|
|
|
|
Раздел 3. Производная и ее приложения |
|
158. |
Найдите промежутки возрастания и убывания функции: |
|
||||||
|
1°) y = 2x3 − 3x2 − 72x + 6 ; |
2°) y = 9x4 −16x3 + 6x2 + 3 ; |
||||||
|
3°) y = |
|
2x |
; |
|
4°) y = x3 + 2x2 − 4x +1 ; |
||
|
x2 +1 |
|
||||||
|
|
|
|
6) у = (х + 3)(х – 1)2; |
||||
|
5) y = 3x4 − 5x3 + 2; |
|||||||
|
7) у = 1 – (х – 5)х3; |
8) у = еx – x + 1; |
||||||
|
9) y = xex; |
t +1 |
|
10*) y = x(ln x – 2); |
||||
|
11*) y = |
|
. |
|
|
|||
|
t2 |
− t + 2 |
|
|
||||
|
|
|
|
|
|
|||
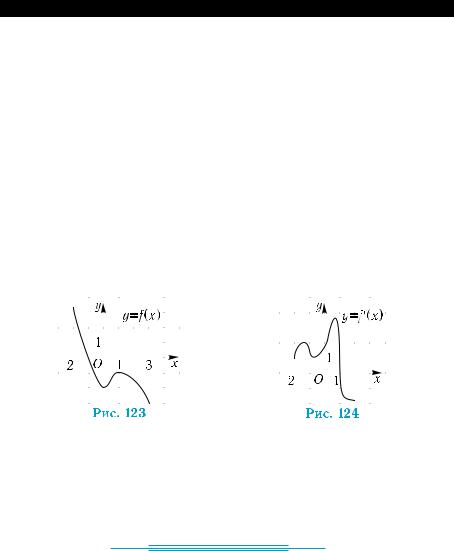
159°. На рис.123 изображен график функции у = f(x), определен- |
||||||||
|
ной на промежутке [–2; 3]. |
|||||||
|
1) Сколько корней имеет уравнение f ′(x) = 0? |
|||||||
|
2) Решите неравенство f ′(x) < 0. |
|||||||
160. |
Функция |
y = f (x) определена на промежутке [–2; 2]. Гра- |
||||||
фик ее производной изображен на рис. 124. Укажите проме- жутки возрастания и убывания функции y = f (x) .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
161. Постройте |
график какой-нибудь непрерывной функции |
|||||||||||||||||||||
у = f(x), удовлетворяющей условию: |
||||||||||||||||||||||
1°) f (x) < 0 |
|
при x < –1 и f (x) = 0 при x > –1; |
||||||||||||||||||||
|
′ |
|
|
|
|
|
|
′ |
||||||||||||||
2) f (x) > 0 при |x| > 1 и f (x) < 0 при |x| < 1. |
||||||||||||||||||||||
′ |
|
|
|
|
|
|
′ |
|||||||||||||||
162*. Докажите, |
что уравнение 4x5 + x3 + 5 = 0 имеет единствен- |
|||||||||||||||||||||
ный корень.
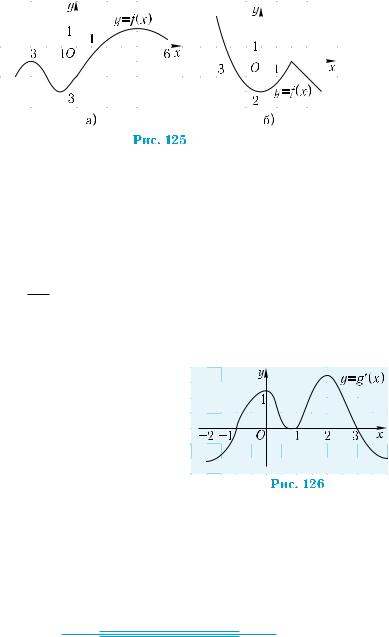
163.Нарис.125,а)–б)изображенграфикфункцииy = f (x) .Найдите: 1°) интервалы, на которых производная данной функции положительна; 2°) интервалы, где производная отрицательна;
3°) точки, в которых производная равна нулю; 4°) точки экстремума функции; 5) точки, в которых производная не существует.
Исследование функций и построение их графиков с помощью производной |
189 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
164. Найдите точки экстремума функции: |
– 5х + 4; |
|||
1°) у = х3 – 2х2 – 7х + 3; |
2°) у = х3 + х2 |
|||
3°) у = х4 – х3 + 7; |
4°) у = (1 + х)ех; |
|||
5°) у = ln x – 3x; |
6) у = х2 – 2 ; |
|
||
|
x2 +4 |
|
x |
|
7) у = |
; |
8) y = 2x ln x; |
|
|
|
|
|||
|
x |
|
|
|
9) y = 4xex .
165.Докажите, что не имеет точек экстремума функция:
|
1) y = 5 x3 + 2x2 |
+ x +1; |
2) |
y = 2x + sin x. |
|
|
3 |
|
|
|
|
166*. На рис. 126 изображен гра- |
|
|
|||
|
фик производной функции |
|
|
||
|
y = g(x) . Найдите: |
|
|
|
|
|
1) точки экстремума функ |
|
|
||
|
ции y = g(x) ; |
|
|
|
|
|
2) наибольшее |
среди |
чисел |
|
|
|
g(2), g(3). |
|
|
|
|
167. |
Постройте график функции: |
|
3) у = х2(2 – х); |
||
|
1) у = х3 – 3х; |
2) |
у = 3х2 – х3; |
||
4) у = х4 – 2х2 + 1; 5) у = 2х4 – 8х; 6) у = х3(3х – 4).
168.Материальная точка движется прямолинейно по закону
x = (t − 3)3 (t −1) −1, где х — координата, t — время (t ≥ 0).
1) Постройте график скорости движения точки.
2) Постройте график закона ее движения.
169*. Сколько корней имеет уравнение х3 – 6х2 + 9х = 4?
190 |
Раздел 3. Производная и ее приложения |
|
||||||||||||||
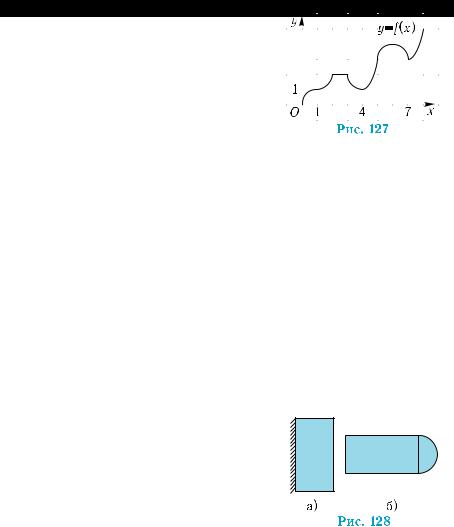
|
170°. На рис. 127 изображен график фун- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
кции у = f(х). Укажите ее наиболь- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
шее и наименьшее значения на про- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
межутке: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) [0; 1]; |
2) [2; 4]; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) [5; 8]; |
4) [0; 7]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
171. Найдите наибольшее и наименьшее |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
значения функции у = f(х) на дан- |
|||||||||||||||
ном промежутке: |
|
|
|
|
2°) у = 2 – 3х, [–1; 3]; |
|
|
|||||||||
1°) |
у = 3х – 2, [–1; 3]; |
|
|
|
|
|
||||||||||
3°) |
у = х2 |
– 6x + 8, [1; 4]; |
|
|
4°) у = х2 |
– 6x + 8, [1; 2]; |
|
|||||||||
5) |
у = |
x3 |
+ х2 – 3x + 1, [–4; 4]; |
6) |
у = |
x3 |
+ х2 – 3x + 1, [–4; 0]; |
|||||||||
|
|
|||||||||||||||
|
|
3 |
|
|
π |
|
|
|
3 |
|
π |
|
π |
|
||
7) |
у = cos x + sin x, |
; |
8) |
|
|
; |
; |
|||||||||
0; |
2 |
|
у = tg x + 2x, − |
|
|
|||||||||||
9*) y = xex, [–2; 0]. |
|
|
|
|
|
|
|
4 |
|
4 |
|
|||||
172. Материальная точка движется вдоль координатной прямой по закону x = − 32 t3 + 32 t2 + 2t − 5, t ≥ 0. Найдите:
1) наибольшую и наименьшую координаты точки за первые две секунды движения; 2) наибольшую и наименьшую скорости точки за первую се- кунду движения.
173*. Из имеющегося материала можно сделать забор длиной 320 м. Опреде- лите:
1) как этим забором огородить пря- моугольный участок наибольшей площади, использовав с одной сторо- ны стенку здания (рис. 128, а);
2) как этим забором огородить стади- он, являющийся прямоугольным полем с полукруговой об-
ластью, присоединенной к одной из его сторон (рис. 128, б), чтобы площадь стадиона была наибольшей?
174*. Какими должны быть размеры закрытой коробки с квадрат- ным основанием, если объем ее должен равняться V и на ее изготовление необходимо потратить наименьшее количест- во материала?
