
978-966-10-2413-6_Matematuka 11_rus
.pdf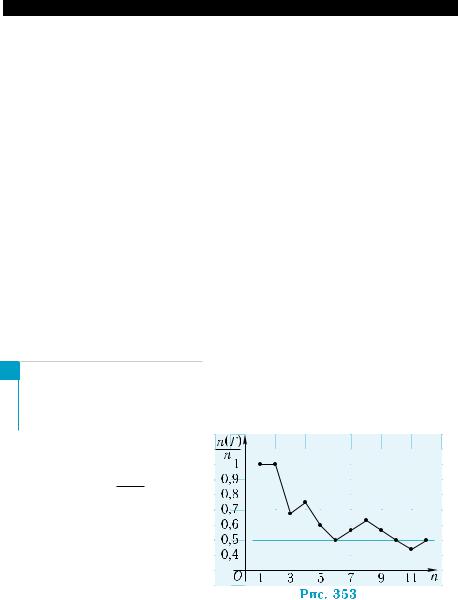
Случайные события и их вероятности |
421 |
рым подсчитывается эта относительная частота. Примеры таких опытов приведены выше (см. таблицу 52). Приведем еще приме- ры статистически устойчивых опытов.
Случайными испытаниями, имеющими статистически устой- чивый характер, является рождение детей. Статистически устой- чивыми опытами являются эксперименты Г. Менделя, связанные с выращиванием гороха (относительная частота прорастания желтого гороха приближенно равна 0,75, зеленого — 0,25). Если проанализировать тексты какой-то книги, то нетрудно обнару- жить, что относительные частоты, например, события «встрети- лась буква о» в достаточно длинных отрывках текста будут близки к числу 0,091.
В результате анализа этих и подобных примеров мы приходим к следующему определению.
Если относительная частота события от серии к серии из большого количества опытов колеблется около некоторого числа, то такие опыты называют статистически устойчивыми, а число, около кото- рого колеблется относительная частота события, принимается за вероятность этого события.
!Наличие у события при определенных условиях веро- ятности, равной р, проявляется в том, что почти в ка- ждой достаточно длинной серии опытов относительная частота события приближенно равна р.
На рис. 353 изображен гра- |
|||
фик |
зависимости |
относи |
|
тельной частоты n(Г) |
появле- |
||
|
n |
подбра |
- |
ния герба при 12 |
|||
сываниях монеты с резуль- |
|||
татами |
ГГЦГЦЦГГЦЦЦГ... |
||
(Г — появление герба, Ц — |
|||
появление цифры) от числа |
|||
подбрасываний п. При п > 10 |
|||
относительная частота колеблется около числа 0,5, которое и при- |
|||
нимают в качестве вероятности события «выпадение герба при од- |
|||
ном подбрасывании монеты». |
|
||
Итак, если говорят, что вероятность некоторого события равна, |
|||
например, 0,82, то это практически означает, что, в среднем, в ка- |
|||

422 Раздел7.Элементытеориивероятностей иматематическойстатистики
ждых 100 опытах, проведенных примерно в одинаковых услови- ях, это событие происходит примерно 82 раза.
Таким образом, каждому событию соответствует число от 0 до 1, называемое вероятностью. Оно показывает, каковы шансы на- ступления данного события в каждом случайном эксперименте.
Пример 5. Некоторое предприятие производит массовую про- дукцию. Если изделие, поступившее в продажу, выходит из строя в течение одного года, то его заменяют запасным. Сколько запа- сных изделий необходимо изготовить, если на протяжении года продают N изделий? Для упрощения предположим, что выход из строя запасного изделия невозможен.
Будем считать, что событие A — «отказ изделия» — имеет некоторую вероятность р. Пусть в течение года вышло из строя m
изделий. Тогда mN — относительная частота события А. Если N —
достаточно большое число, то mN ≈ p. Отсюда m ≈ N p . На практи-
ке довольно часто вероятность р неизвестна. Для ее оценки (при- ближенного вычисления) проводят некоторое число п испытаний изделий в течение года. Если за это время откажет k изделий, то
k n
значении п можем считать, что nk ≈ p. Тогда m ≈ Nkn . ■
Подобные методы используют при оценивании урожая на поле по урожаю на некотором количестве небольших участков; плотно- сти минералов по результатам взвешивания некоторого количест- ва образцов; влажности зерна на приемных пунктах; волокнисто- сти хлопка и т. п.
99 Контрольные вопросы
1.Игральный кубик подбрасывался трижды, при этом выпало, соответственно, 2, 2, 5 очков. Можно ли по этим данным ука- зать приближенное значение вероятности события: «при под- брасывании игрального кубика выпало два очка»?
Вероятность наступления события A в некотором опыте равна 0,72. Можно ли утверждать, что в 100 таких же опытах, прове- денных в тех же условиях, это событие наступит ровно 72 раза?

Случайные события и их вероятности |
423 |
3.Для контроля за качеством продукции некоторого завода из каждой партии готовых изделий отбирают на проверку 150 деталей. Проверку не выдерживают, в среднем, 6 деталей. Как оценить вероятность выпуска бракованных деталей заво- дом: а°) в настоящее время; б) после совершенствования тех- нологии производства?
4.Зная относительную частоту события, охарактеризуйте соот- ветствующее явление:
а) относительная частота реализованных пенальти для дан- ного футболиста равна 0,8; б) относительная частота пенальти, взятых данным вратарем, равна 0,2;
в) относительная частота рабочих дней на предприятии, в ко- торых достигалась намеченная цель, равна 0,88; г) относительная частота обнаружения бракованной детали рентгеном равна 0,8.
Задачи
359°. Какие из следующих испытаний можно считать случайными: 1) страхование транспортных средств; 2) олимпийские игры; 3) инвестиционная деятельность банков;
4) распространение эпидемий;
5) запуск космического корабля;
6) передача генов от родителей к потомкам? 360°. Какие из последующих событий — случайные:
1) за период страхования автомобиль не попал ни в одну аварию; 2) на олимпийских играх команда Украины заняла второе место;
3) фирма, которую инвестировал банк, не возвратила кредит; 4) эпидемия была быстро локализована; 5) ребенок унаследовал от обоих родителей гены одного типа?
361. В шкатулке лежат несколько одинаковых по размеру кату- шек с нитками трех цветов: черного, белого и коричневого. Из шкатулки взяли наугад 4 катушки ниток. Будут ли сре- ди взятых катушек наверняка:
1) хотя бы две с черными нитками;
2) хотя бы две с нитками одного цвета;
3) хотя бы три с черными нитками;
4) хотя бы три с нитками одного цвета?
424 Раздел7.Элементытеориивероятностей иматематическойстатистики
Приведите примеры случайных, в частности достоверных, невозможных событий, связанных с рассмотренным опытом.
362. В сумке лежат одинаковые по форме конфеты двух сортов: 9 конфет первого сорта и 6 конфет второго сорта. Не глядя, из сумки вынули 8 конфет.
1) Будет ли среди них наверняка хотя бы одна конфета пер- вого сорта?
2) Будет ли среди них наверняка хотя бы одна конфета вто- рого сорта?
3) Сколько конфет нужно вынуть из сумки, чтобы среди них наверняка были конфеты первого сорта?
4) Сколько конфет нужно вынуть из сумки, чтобы среди них наверняка были конфеты обоих сортов?
Приведите примеры случайных, в частности достоверных, невозможных событий, связанных с рассмотренным опытом.
363°. Урна содержит 10 белых и 8 черных шаров. Из урны на угад берут один шар. Какова вероятность того, что он будет: 1) черным; 2) белым?
364°. Из тщательно перемешанной колоды из 36 карт наугад бе- рут одну карту. Какова вероятность того, что она окажется: 1) пиковой масти; 2) тузом; 3) красной масти; 4) «картинкой» (то есть или валетом, или дамой, или королем, или тузом)?
365°. Из набора домино, содержащего 28 камней, наугад берется один камень. Какова вероятность того, что он: 1) будет содер- жать 6 очков; 2) окажется дублем; 3) окажется не дублем?
366°. Из букв слова математика наугад берут одну букву. Како- ва вероятность того, что это окажется: 1) буква м; 2) буква а; 3) гласная буква; 4) согласная буква?
367. Числа от 1 до 15 написаны на 15 карточках по одному на каждой. Выбирают наугад одну карточку. Чему равна веро- ятность того, что написанное на этой карточке число: 1) де- лится на 5; 2) является четным; 3) является нечетным; 4) яв- ляется точным квадратом; 5) двузначное; 6) простое?
368. Подброшены два правильных игральных кубика. Какова вероятность того, что сумма выпавших очков будет: 1) чет- ной; 2) меньше 5; 3) больше 8; 4) простым числом; 5) делить- ся на 3?

Случайные события и их вероятности |
425 |
369.В ящике белые и черные шарики. Белых шариков 10. Из- вестно, что вероятность извлечь белый шарик при случай- ном извлечении одного шарика равна 72 . Сколько черных шариков в ящике?
370.В слове 8 гласных букв. Известно, что вероятность натол- кнуться наугад на гласную букву в слове равна 0,4. Сколько всего букв в этом слове?
371.В ящике в три раза больше красных шаров, чем черных (шары одинаковы во всем, кроме цвета). Наугад вынима- ют один шар. Какова вероятность того, что он: 1) красный; 2) черный?
372°. В любой книге на средней странице выберите 10 полных строк текста. Подсчитайте количество гласных букв и, в частности, буквы «е» в каждой из строк. Какой в среднем процент всех букв строки составляет: 1) буква «е»; 2) гласная буква? Выполните подобный опыт с другой книгой и сравни- те результаты.
373°. Сколько раз промахнулся стрелок в 50 выстрелах, если от- носительная частота попаданий равна 0,7?
374°. Относительная частота проданных в магазине за день пар обуви для взрослых равна 0,6. В этот день продали 24 пары детской обуви. Сколько всего пар обуви продали в этот день?
375. Проводятся последовательные подбрасывания правильной монеты, после каждого из которых подсчитывается относи- тельная частота события «выпал герб». Какие из приведен- ных ниже числовых последовательностей могут соответство- вать указанному опыту:
1) |
1 ; |
1 ; |
2 ; |
3 ; |
4 |
; ... ; |
2) |
1 |
; 1 ; 1; |
3 |
; |
3 |
; |
...; |
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
2 |
4 |
|
5 |
|
|
3) |
|
|
1 |
1 |
2 |
|
4) |
1 |
1 |
3 |
|
4 |
|
|
0; |
0; |
3 ; |
2 ; |
5 ; |
...; |
2 |
; 1; 3 ; |
4 |
; |
5 |
; |
... ? |
||
376°. Для проверки качества было исследовано 200 деталей, |
||||||||||||||
среди которых 5 оказались бракованными. Какой можно |
||||||||||||||
считать вероятность того, что наугад взятая деталь будет: |
||||||||||||||
1) |
пригодной; 2) бракованной? Сколько бракованных дета- |
|||||||||||||
лей окажется, в среднем, в партии из 1000 деталей?

426 Раздел7.Элементытеориивероятностей иматематическойстатистики
377°. Вероятность того, что в наугад взятой семье некоторого по- селка есть телевизор, равна 0,998.
1) Сколько, в среднем, телевизоров будет в 500 семьях этого поселка?
2) Сколько приблизительно опросили семей в этом поселке, если насчитали 1497 телевизоров?
378. Выполните опыт с подбрасыванием игрального кубика 100 раз, записывая все результаты опыта. Результатом будем считать число выпавших очков. Их можно записать в такую таблицу.
№ опыта |
1 |
2 |
3 |
4 |
5 |
... |
Число очков |
3 |
5 |
2 |
3 |
1 |
... |
Вычислите относительную частоту появления каждого чи- сла очков. Подтверждают ли подсчеты предположение о том,
6?
379.Выпущено сто лотерейных билетов с одиннадцатью денеж- ными выигрышами, из которых восемь — по 10 грн., два — по 50 грн. и один — 100 грн. Из купленных 25 билетов три выиграли по 10 грн. и один выиграл 50 грн. Остальные были без выигрыша. Найдите вероятность и относительную частоту события: 1) «купленный билет безвыигрышный»;
2)«на приобретенный билет выпадает выигрыш 10 грн., 50 грн., 100 грн.». Сравните вероятности этих событий с со- ответствующими относительными частотами.1
Упражнения для повторения
380.Во время встречи четверо приятелей пожали друг другу руки. Сколько было рукопожатий?
381.Сколько существует трехзначных чисел, составленных из цифр 0, 4, 8, если: 1) цифры не повторяются; 2) цифры могут повторяться?
382.Сколькими способами можно распределить 4 карандаша между двумя детьми, если: 1) карандаши различны; 2) ка- рандаши одинаковы?

Случайные события и их вероятности |
|
427 |
|
Итог |
|
|
|
Основные понятия |
|
|
|
|
|
|
|
Определение |
Примеры, формулы |
||
Под случайным испытанием понимают |
Извлечение шарика из |
|
|
любое действие, которое можно повто- |
урны. |
|
|
рить большое количество раз примерно |
Предоставление скорой |
|
|
в одинаковых условиях и результаты |
медицинской помощи. |
|
|
которого предсказать невозможно. |
|
|
|
Любой исход случайного испытания |
Извлекли из урны бе- |
|
|
называется случайным событием. |
лый шарик. |
|
|
|
На станцию скорой по- |
|
|
|
мощи поступило 10 вы- |
|
|
|
зовов. |
|
|
Если испытание заканчивается одним |
P( A) = |
N( A) . |
|
из N равновозможных исходов, из кото- |
|
||
рых N(A) исходов приводят к наступле- |
|
N |
|
нию события А, то вероятностью собы- |
|
|
|
тия А называют отношение N( A) . |
|
|
|
N |
|
|
|
Число опытов m, в которых произошло |
ν( A) |
= m . |
|
некоторое событие, называется часто- |
|
||
той этого события. Отношение числа |
|
n |
|
опытов, в которых произошло некото- |
|
|
|
рое событие, к общему числу опытов n, |
|
|
|
проведенных в тех же условиях, назы- |
|
|
|
вается относительной частотой этого |
|
|
|
события. |
|
|
|
Если относительная частота события от |
P( A) ≈ ν( A). |
|
|
серии к серии из большого числа опы- |
|
|
|
тов колеблется около некоторого числа, |
|
|
|
то такие опыты называют статистиче- |
|
|
|
ски устойчивыми, а число, около кото- |
|
|
|
рого колеблется относительная частота |
|
|
|
события, принимается за вероятность |
|
|
|
этого события. |
|
|
|

428 Раздел7.Элементытеориивероятностей иматематическойстатистики
Основные утверждения
|
|
Вероятность невозможного события V равна 0. |
P(V ) = 0. |
Вероятность достоверного события U равна 1. |
P(U) =1. |
Вероятность любого случайного события A нахо- |
0 ≤ P(A) ≤ 1. |
дится между 0 и 1. |
|
Относительная частота невозможного события V |
ν(V ) = 0. |
равна 0. |
|
Относительная частота достоверного события U |
ν(U) = 1. |
равна 1. |
|
Относительная частота любого случайного события |
0 ≤ ν( A) ≤ 1. |
A находится между 0 и 1. |
|
§21. Элементы комбинаторики
В данном параграфе изучаются методы вычисления числа различных комбинаций из заданных объектов, удовлетворяющих тем или иным условиям. Такие задачи называются комбинаторными.
.Комбинаторное правило умножения
Рассмотрим опыт, число исходов которого сложно подсчитать перебором.
Пример 1. В пригородный поезд из девяти ваго- 4 лица, произвольно выбирая вагоны. Какова вероят-
ность того, что они окажутся в разных вагонах?
Исходы опыта, описанного в примере, являются наборами но- меров вагонов, выбранных 4 лицами. Выписать все исходы опыта (а их свыше 6000) довольно трудно. Необходимо иметь специаль- ные методы, позволяющие подсчитать число исходов.
Один из способов решения этой задачи основан на так называ- емом основном правиле комбинаторики. Прежде чем формулиро- вать его, рассмотрим следующий пример.
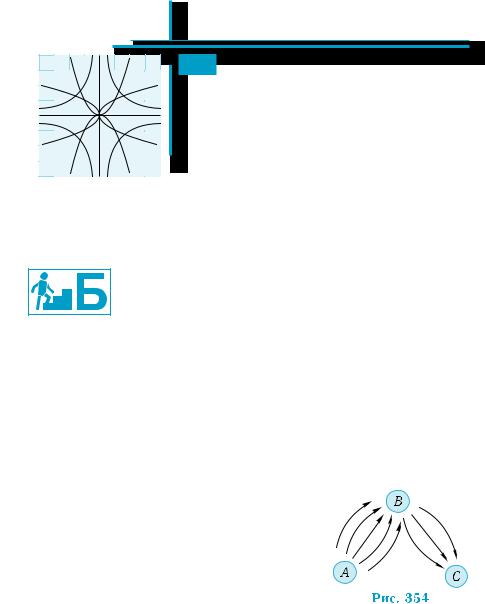
Пример 2. Из города А в город В ведут пять дорог, а из В в С — три. Сколько дорог, проходящих через В, ведут из А в С?
Для каждого из пяти способов добрать- ся из города А в город В существует три спо- соба доехать из В в С (рис. 354). Следова-
тельно, из А в С можно добраться 5 3 = 15 способами. g
Ответ. 15 дорог.
Метод решения, использованный в примере 2, допускает обоб щение. Соответствующее утверждение называется основным
430 Раздел7.Элементытеориивероятностей иматематическойстатистики
правилом комбинаторики, или комбинаторным прави-
лом умножения.
Термин «комбинаторика» происходит от латинско- го слова combina — соединять.
Правило умножения. Если объект А можно вы- брать m способами и если после каждого такого вы- бора объект В можно выбрать n способами, то выбор пары (А, В) можно осуществить m·n способами.
!Обратите внимание на то, каким бы способом не был выбран объект А, второй объект должен выбираться одинаковым числом способов.
 Обобщим рассмотренное правило умножения.
Обобщим рассмотренное правило умножения.
 Если объект А1 может быть выбран n1 раз- личными способами, объект А2 — n2 различ- ными способами и так далее, объект Аk —
Если объект А1 может быть выбран n1 раз- личными способами, объект А2 — n2 различ- ными способами и так далее, объект Аk —
nk различными способами, то k объектов А1, А2, ..., Аk можно выбрать n1 × n2 × . . . × nk способами.
Решим теперь пример 1.
Для вычисления искомой вероятности необходимо вычислить общее число исходов опыта и число тех из них, из которых состоит событие, вероятность которого вычисляется. Подсчитаем число спо- собов, с помощью которых 4 лица могут выбрать для себя вагоны из 9 вагонов поезда. Первое лицо может выбрать любой из 9 вагонов. Какой вагон не был бы выбран, второе лицо будет иметь тоже 9 воз- можностей для выбора. Следовательно, два лица могут выбрать ва- гоны 9 9 = 81 способом. Рассуждая также далее, придем к выводу, что общее число исходов рассматриваемого опыта равно 94 = 6561.
Событие А «4 лица окажутся в разных вагонах» состоит из исхо- дов опыта, где все вагоны различны. Первое лицо может выбрать вагон 9-ю способами. Для любого его выбора второе лицо будет иметь лишь 8 возможностей (в один из вагонов он уже не может попасть), следовательно, два лица могут выбрать вагоны 9 8 = = 72-я способами. Продолжая аналогично далее, получим, что об- щее число исходов опыта, при которых наступает событие А, рав-
но: N ( A) = 9 8 7 6 . Все исходы равновозможны, так как вагоны выбираются наугад. Поэтому
