
Конспект лекций Высшая математика (Басканова)
.pdf
862
y1 y2 M1 f y x, y1 y1 y2 y1 y21 Mm y1 y2 y1 , y2 ,
где 0 1. Следовательно, для любой точки y0 C последовательность
y1 Ay0 , y2 Ay1 , сходится и lim yn y есть единственное непрерывное
n
решение уравнения (7.6.5), определенное на отрезке a,b , и его последовательными приближениями являются функции y0 , y1 , y2 , . Полученная при
этом оценка имеет вид
y y y yn n 10 1 .
Доказанная теорема существования неявной функции находит себе следующее практическое применение: пусть требуется вычислить значение непрерывной функции y y x для данного значения аргумента в том случае,
когда непосредственное вычисление этого значения затруднительно. Тогда записывают данную функцию в неявном виде f x, y 0, и если
f x, y непрерывная и имеет ограниченную производную по y:
то |
|
|
|
|
|
|
|
0 m |
|
f y |
|
M , |
||||||
|
|
|
|
|
|
|
|
|||||||||||
f x, yn f x, yn f x, y yn y f y x, n , |
||||||||||||||||||
|
||||||||||||||||||
где |
|
|
|
n y q y yn , |
0 q 1, |
|||||||||||||
|
|
|
|
|
||||||||||||||
откуда получают: y yn |
|
f x, yn |
|
. |
|
|
|
|
|
|
|
|
||||||
|
f y x, n |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Значение n неизвестно, его заменяют приближенным значением |
|||||||||||||||||
n |
yn и далее пользуются итерационной формулой |
|||||||||||||||||
|
|
|
|
|
yn 1 yn |
f x, yn |
|
, |
n 1,2, |
|||||||||
|
|
|
|
|
f y x, yn |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Так, например, для вычисления квадратного корня из числа рассматри- |
|||||||||||||||||
вают функцию F x, y y2 |
x 0 , формула для которой приобретает вид |
|||||||||||||||||
|
|
1 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||
|
yn 1 |
|
|
|
|
n 1,2, |
(процесс Герона). |
|||||||||||
|
|
|
|
|
||||||||||||||
|
2 |
yn |
|
|
, |
|||||||||||||
|
|
|
|
yn |
|
|
|
|
|
|
|
|
||||||
Если в этой формуле положить y0 1,4, то уже на втором шаге полу-
чают результат с точностью до 10 7 . Метод итерации широко применяется в вычислительной технике.
863
Заметим, что для итерационных процессов справедливо утверждение: последовательность элементов xn 1 u xn является фундаментальной.
Для доказательства существования решения какого-либо уравнения с помощью принципа сжатых отображений достаточно:
1)рассмотреть соответствующий этому отображению оператор;
2)показать, что этот оператор отображает полное метрическое пространство в себя;
3)убедиться, что этот оператор является сжатым.
7.2.7 Линейные пространства
При построении метрических пространств мы сосредоточили внимание только на одном важном свойстве множества вещественных чисел – на наличии расстояния в нем. Если рассматривать алгебраические операции, определенные в множестве вещественных чисел, то можно прийти к понятию линейного пространства.
Пусть X - множество элементов некоторой природы, удовлетворяющее следующим аксиомам:
1. X – абелева группа относительно групповой операции сложения. Это значит, что определена сумма x+y двух любых элементов x, y X ,
являющаяся элементом того же множества, причем операция сложения обладает следующими свойствами:
x+y=y+x – закон коммутативности; x+(y+z)=(x+y)+z – закон ассоциативности;
Существует нулевой элемент 0 X такой, что x 0 x для любого x
из X.
Для каждого элемента x X существует обратный элемент (-x) того же пространства такой, что x+(-x)=0.
2. Определено умножение элементов x, y, z,... множества X на вещественные (комплексные) числа , , , причем x является снова элементом
множества X и выполнены условия:
( x) ( )x – закон ассоциативности;
(x y) x y - закон дистрибутивности;
1 x x .
Множество X, удовлетворяющее аксиомам 1 и 2, называется линейным (или векторным) пространством. В зависимости от того, на какие числа, вещественные или комплексные, допускается умножение элементов множества X, мы получаем вещественное или комплексное линейное пространство.
Приведем примеры линейных пространств.
1. Совокупность Rn вещественных n-мерных векторов образует вещественное линейное пространство.
864
2. Совокупность комплекснозначных решений обыкновенного однородного линейного дифференциального уравнения n-го порядка образует комплексное линейное пространство.
3. Совокупность элементов вещественного (комплексного) класса Lp a,b образует вещественное (комплексное) линейное пространство.
4. В арифметическом пространстве R1 элементы (действительные числа) можно складывать и умножать на действительные числа, не выходя за пределы пространства R1 : если x, y R1 , то x y R1 , ax R1 где a - дейст-
вительное число.
5.В пространстве C a,b непрерывных на отрезке a,b функций f (x)
врезультате операций f1 (x) f2 (x), c f (x) вновь получаем непрерывные
функции.
6. Пусть E - совокупность последовательностей x x1 , x2 ,... таких, что
xk2 .
k 1
Пусть x y x1 y1 , x2 y2 ,... , ax ax1 ,ax2 ,... .
Покажем, что E - линейное векторное пространство. Действительно,
|
xk yk 2 |
|
|
|
|
|
|
|
|
2 xk2 |
2 yk2 |
, |
|||||
k 1 |
|
|
|
k 1 |
|
|
k 1 |
|
|
|
axk |
2 |
|
|
|
|
|
|
|
a |
2 xk2 |
. |
|
|||
|
k 1 |
|
|
|
k 1 |
|
|
|
Таким образом, элементы x+y и ax принадлежат E, если x и y принадлежат E. Проверка аксиом не представляет труда.
Рассмотрим множества, не являющиеся линейными пространствами.
1.Множество всех векторов пространства, за исключением векторов, коллинеарных некоторой прямой l (так как в пределах этого множества нельзя складывать векторы, симметричные относительно указанной прямой l).
2.Множество всех многочленов степени, точно равной натуральному
числу n ( 2x таких многочленов может оказаться многочленом степени ниже
n).
Множество всех многочленов степени, не превышающей натурального числа n, коэффициенты которых положительны (элементы такого множества нельзя умножить на отрицательные вещественные числа).
7.2.8. Норма и скалярное произведение
Если при построении пространств есть такие важные свойства множества вещественных чисел как наличие расстояния и наличие алгебраических операций, то можно прийти к определению нормированных пространств.


867
Теорема 10 (тождество параллелограмма). Пусть L – нормированное пространство. На L можно ввести скалярное произведение, согласованное с нормой тогда и только тогда, когда в L выполнено тождество параллелограмма:
x, y L 
 x y
x y
 2
2 
 x y
x y
 2 2
2 2 
 x
x
 2
2 
 y
y
 2 .
2 .
7.2.9 Гильбертово пространство
Определение 17. Нормированное пространство называется банаховым, если оно является полным относительно метрики, порожденной нормой.
Определение 18. Пространство со скалярным произведением называется гильбертовым, если оно полно относительно метрики, порожденной скалярным произведением.
Замечание. Гильбертово пространство является непосредственным обобщением евклидова пространства, так как оно обладает наибольшим числом свойств евклидова пространства. Поэтому теория гильбертовых пространств выделилась в самостоятельную ветвь функционального анализа специфичными методами и результатами, не укладывающимися в общие рамки нормированных пространств. Результаты теории гильбертовых пространств глубже и полнее, чем результаты теории других пространств.
Примером гильбертовых пространств могут служить L2 и l2 . Определение 19. Система векторов в гильбертовом пространстве на-
зывается ортогональной, если  xi , x j
xi , x j  0 при i j . Если, кроме того,
0 при i j . Если, кроме того,
 xi , x j
xi , x j  1 при i j , то система называется ортонормированной.
1 при i j , то система называется ортонормированной.
Определение 20. Элемент x называется ортогональным к множеству X, если он ортогонален каждому элементу этого множества. Множества X и F называются ортогональными, если каждые два элемента этих множеств попарно ортогональны.
Ортогональные элементы обладают следующими свойствами. 1. Если x y1 и x y2 , то x 1 y1 2 y2 , а, следовательно,
x1 , 1 y1 2 y2 1 x1 , y1 1 x2 , y2 0 .
2. Если xn x и xn x0 , то x0 x . Из этих свойств вытекает
Следствие: если x X , то x L(X ) .
Теорема 11. Чтобы система элементов xk была полной в гильбертовом пространстве H, т.е. чтобы L xk H , необходимо и достаточно, чтобы не существовало элемента xk 0 и элемента x0 xk для всех k.
Определение 21. Полная ортонормированная система элементов называется ортонормированным базисом гильбертова пространства.

868
Пример 7. Доказать, что в пространстве l1 |
x x1 , x2 |
|
xn |
|
с |
,... : |
|
||||
нормой |
|
n 1 |
|
|
|
|
|
|
|
|
x xn
n 1
нельзя ввести согласованное с этой нормой скалярное произведение. Доказательство. Покажем, что в l1 не выполняется равенство паралле-
лограмма

 x y
x y
 2
2 
 x y
x y
 2 2
2 2 
 x
x
 2
2 
 y
y
 2 .
2 .
Для этого возьмем x (1,1,0,0,...) , y (1, 1,0,0,...) .
Тогда

 x
x
 2 ,
2 , 
 y
y
 2 ,
2 , 
 x y
x y
 2,
2, 
 x y
x y
 2
2
и

 x y
x y
 2
2 
 x y
x y
 2 8 2
2 8 2 
 x
x
 2
2 
 y
y
 2 16,
2 16,
т.е. равенство параллелограмма не выполнено.
Пример 8. В линейном пространстве H непрерывных на [0, ) функ-
ций x(t) таких, что |
|
x(t) |
|
2 e t dt сходится, положим |
|
|
|||
|
0 |
|
|
|
|
|
|
x, y x(t) y(t)e t dt . |
|
0 |
Проверить выполнение аксиом скалярного произведения. |
|
Решение. |
|
|
|
1. x, x x(t)x(t)e t dt 0 |
x H . |
0 |
|
|
|
|
|
Если x, x 0 , то x(t) e t 2 dt 0 |
и x(t) непрерывна, то по свойству ин- |
||
0 |
|
|
|
теграла Римана x(t) 0 . Если же x(t) 0 , то очевидно, что |
x, x 0 . Таким |
||
образом, для любого x H |
x, x 0 и |
x, x 0 x=0. |
|
2. x, y x(t) y(t)e t dt y, x , причем интеграл сходится для любых
0
x, y H , так как для любого конечного T>0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
T |
t |
dt |
|
T |
2 |
(t)e |
t |
T |
2 |
(t)e |
t |
2 |
. |
|
|
x(t) y(t)e |
|
x |
|
|
dt y |
|
|
dt |
|||||
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. x, y |
x(t) y(t)e t dt |
x(t) y(t)e t dt x, y . |
|
||||||||||||
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|


870
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ ДЛЯ САМОПРОВЕРКИ
1.Дать определение функции комплексного переменного (однозначной, многозначной)
2.Могут ли у двух различных функций комплексного переменного
быть
а) различные действительные части и одинаковые мнимые части; б) одинаковые действительные части и различные мнимые части; в) одинаковые действительные части и одинаковые мнимые части; г) различные действительные части и различные мнимые части;
3.Верно ли, что ez 0 при любом z C ?
4. Существуют ли такие точки z C , что cos z 1?
5.Верно ли, что функция sin z не ограничена на С?
6.Дать определение производной функции f(z) в точке z
7.Критерий дифференцируемости функции комплексного переменного
8.Дать определение аналитической (голоморфной) функции в точке и в
области
9.Дать определение особых точек
10.Определение дифференциала аналитической функции
11.Может ли функция быть дифференцируемой в точке z0 и не быть
аналитической в этой точке?
12.Может ли функция быть аналитической только в одной точке?
13.Верно ли, что функция f (z) аналитическая в области D, если
Re f (z) и Im f (z) – функции, гармонические в этой области?
14.Дать определение интеграла от функции f(z) по контуру L
15.Перечислить свойства интеграла от функции комплексного пере-
менного
16.Сформулировать теорему Коши и ее следствия
17.Сформулировать интегральную формулу Коши
18.Дать определение ряда Тейлора функции f(z) в точке z0
19. Если f (z)dz 0 , следует ли из этого, что f (z) – аналитическая
L
функция внутри замкнутой кривой L?
20. Дать определение нулей функции (простой нуль и нуль кратности
m)
871
21. Дать определение ряда Лорана, указать правильную и главную части ряда Лорана
22. |
Дать классификацию особых точек |
|
23. |
Может ли разложение некоторой функции в ряд Лорана содержать: |
|
а) конечное число слагаемых с отрицательными степенями z z0 ; |
||
б) конечное число слагаемых с положительными степенями z z0 ; |
||
в) бесконечное число слагаемых с отрицательными степенями z z0 ; |
||
г) конечное число слагаемых с положительными степенями z z0 ? |
||
24. |
Может ли точка z0 быть особой точкой указанных типов для дан- |
|
ных функций: |
|
|
а) полюсом для f (z) и полюсом для z z0 f (z) ; |
||
б) полюсом для |
f (z) и устранимой особой точкой для z z0 f (z) ; |
|
в) полюсом для |
f (z) и существенно особой точкой для z z0 f (z) ; |
|
25.Дать определение вычета функции f (z) в точке z0 .
26.Сформулировать теорему о сумме вычетов и теорему Коши (основную теорему о вычетах)
27.Дать определение метрики и метрического пространства
28.Привести примеры метрических пространств
29.Привести аксиомы расстояния
30.Дать определение фундаментальной последовательности
31.Ввести в трехмерное пространство метрику, отличную от евклидовой, удовлетворяющую аксиомам метрики
32.Может ли быть, что при введении метрик в множество различные элементы в одной метрике окажутся совпадающими в другой метрике?
33.Дать определение полного пространства
34.Привести примеры полных и неполных пространств
35.Ввести на прямой , метрику по формуле (x, y) |arctg x-
arctg y|. Будет ли это пространство полным?
36.Построить метрические пространства, обладающие и не обладающие свойством полноты
37.Сформулировать принцип сжимающих отображений
38.Дать определение оператора сжатия
39.Привести примеры применения принципа сжатых отображений
40.Дать определение нормированного пространства
41.Привести аксиомы скалярного произведения
42.Сформулировать тождество параллелограмма
43.Дать определение банахова пространства
44.Дать определение гильбертова пространства




 - норма этого элемента, удовлетво-
- норма этого элемента, удовлетво-


 0 , норма любого элемента x не отрицательна, причем
0 , норма любого элемента x не отрицательна, причем 


 0 тогда и только тогда, когда
0 тогда и только тогда, когда 
 x
x


 x
x












 – неравенство треугольника.
– неравенство треугольника.


 . Если расстояние определено по
. Если расстояние определено по


 max
max





 , принимаю-
, принимаю-
 0 ,
0 , 
 0
0 
 ;
;
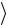





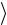

 .
.
 может принимать комплексные значе-
может принимать комплексные значе-


 заменяется более общим требованием
заменяется более общим требованием 


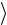 , где звездочка обозначает комплексное сопряжение.
, где звездочка обозначает комплексное сопряжение.
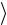

 ,
,