Конспект лекций Высшая математика (Басканова)

772

где cos n, x , cos n, y , cos n, z – направляющие косинусы нормали к поверхности, d – мера элемента поверхности. Пусть поверхность q , через

которую вычисляется поток, проектируется взаимно-однозначно на плоскость xOy , т.е. ее уравнение можно однозначно разрешить относительно z :

z f (x, y). Проекция элемента поверхности на xOy равна dxdy d cos n, z .

Отсюда следует, что

d dxdy . cos n, z

Подставляя найденное значение для d в координатную форму потока и заменяя z его зависимостью от x и y из уравнения поверхности, получим

двойной интеграл по области qxoy :

П=

P x, y, z(x, y) cos(n, x) Q x, y, z(x, y) cos(n, y) R x, y, z(x, y) cos(n, z)

qxoy

dxdy . cos(n, z)

Направляющие косинусы нормали к поверхности q выражаются через ее уравнение по формулам

Таким образом, вычисление потока свелось к вычислению одного двойного интеграла по области qxoy .

Аналогично, поток векторного поля можно свести к двойному интегралу по области qxoz . При этом поверхность q проецируют на координатную

плоскость xOz , а ее уравнение решают относительно y : y y(x, z) . Мера

элемента поверхности d будет выражаться через его проекцию на плоскость xOz по формуле

d dxdz . cos n, y

Поток векторного поля через поверхность q равен двойному интегралу по области qxoz :

773

П=

P x, y(x, z), z cos(n, x) Q x, y(x, z), z cos(n, y) R x, y(x, z), z cos(n, z)

qxoz

dxdz . cos(n, y)

Направляющие косинусы нормального вектора к поверхности q находят из ее уравнения следующим образом:

И, наконец, если поверхность проектируется однозначно на плоскость yOz , то ее уравнение нужно решить относительно x : x x( y, z) .

В этом случае вычисление потока сводится к вычислению двойного интеграла по области qyoz :

Пример 1. Вычислить поток векторного поля F 4i 5 j 2k через поверхность q в сторону, определяемую вектором единичной нормали n к поверхности q , если q – часть плоскости x 2y 3z 6 , расположенная в октанте x 0, y 0, z 0 , а n образует острый угол с осью Oz .

Решение. Известно, что нормальным вектором к плоскости является вектор, координаты которого есть коэффициенты при неизвестных в уравнении плоскости. В нашем случае – это вектор m(1,2,3) . Поскольку

mF 1 4 2 ( 5) 3 2 0, то нормаль m к плоскости (а, значит, и единич-

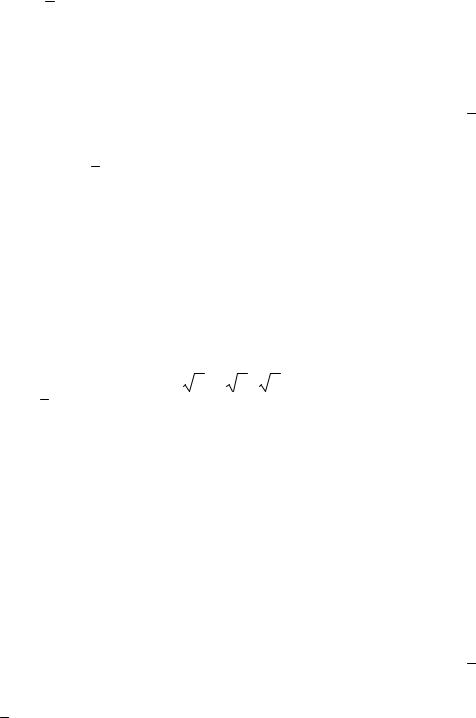
774

ная нормаль n к этой плоскости) перпендикулярна векторному полю. Но тогда

ПF nd 0 d 0.

йй

Пример 2. Вычислить поток векторного поля F(0, y,0) через поверхность q в сторону, определяемую вектором единичной нормали n к поверхности q , если q – часть плоскости 1 x y z 0 , расположенная в октанте x 0, y 0, z 0 , а n образует острый угол с осью Oz .

Решение.

Поток найдем методом проектирования на три координатные плоскости. Для этого воспользуемся формулой (6.3.2). Имеем:

П Pdydz Qdzdx Rdxdy ydzdx.

довательно, n образует острый угол с осью Oz и тупой угол с осью Oy ). Поэтому при сведении поверхностного интеграла к двойному по области Dxz перед двойным интегралом необходимо поставить знак минус:

Пример 3. Вычислить поток векторного поля F(1,1, z) через поверхность q в сторону, определяемую вектором единичной нормали n к поверхности q , если q – часть параболоида z x2 y2 , удовлетворяющая условию

z 1, а n – внешняя нормаль к параболоиду.

Решение. Изобразим поверхность q вместе с требуемой в условии задачи нормалью на рис. 6.3.5.

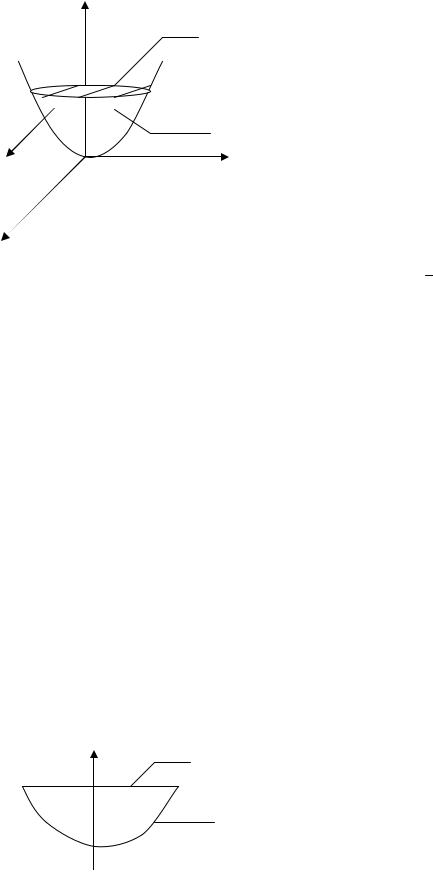
777

q

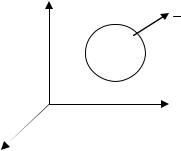
Рис. 6.3.8. Замкнутая поверхность в потоке жидкости

Пример 4. Представим мысленно, что замкнутая поверхность q распо-

ложена в равномерном потоке текущей жидкости и жидкость свободно проникает через ее стенки (рис. 6.3.8).

Поток изнутри поверхности q будет равен нулю, так как сколько вте-

кает жидкости в данную поверхность, столько и вытекает.

Вернемся к произвольному векторному полю, заданному в области D . Найдем количество векторных линий этого поля, которые возникают в единицу времени в единице объема V , заключенного внутри поверхности q .

Очевидно, что оно равно величине потока изнутри поверхности, деленной на объем, т.е.

П q F,n0 d . V V

Данное отношение, определяющее количество возникающих векторных линий в единице объема, характеризует среднюю объемную мощность источника, или мощность стока (для отрицательных потоков изнутри поверхности q ).

Чтобы найти, сколько образуется векторных линий в единицу времени

вточке P0 , нужно перейти к пределу при q P0 , т.е. при стягивании объема

вточку P0 .

Предел, если он существует, называют дивергенцией, или расхождени-

q P0 V

Определение 4. Дивергенция (или расходимость) – это скалярная ве-

личина, характеризующая мощность источников или стоков векторного поля в каждой его точке. Она равна пределу потока векторного поля через замкнутую поверхность, отнесенного к объему, заключенному внутри поверхности, при стягивании поверхности в точку.

Если векторное поле в области D задано тремя скалярными функциями – проекциями вектора поля на координатные оси

778

F P(x, y, z), Q(x, y, z), R(x, y, z) ,

то дивергенцию поля в произвольной точке M находят по формуле

всех точках области имеют непрерывные частные производные.

Замечание 1. В формуле (6.3.5) не пишут индекс M , так как эта формула справедлива в любой точке поля.

Замечание 2. Для плоского поля в правой части формулы (6.3.5) отсутствует третье слагаемое.

Отметим некоторые свойства дивергенции.

1.Если a – постоянный вектор, то div a 0.

2.div a b div a + divb , где и – произвольные постоян-

ные.

Пример 5. Найти дивергенцию однородного поля a const. Решение. Проекции вектора поля на координатные оси

ax const, ay const, az const

имеют вид

div a ax ay az 0.

x y z

Однородное поле не имеет источников. Пример 6. Найти дивергенцию радиус-вектора.

Решение. Координаты радиус-вектора r ix jy kz .

div r x y z 1 1 1 3.

x y z

Каждая точка поля радиус-вектора является источником мощности 3. Пример 7. Доказать равенство div f F grad f F f div F .

Решение. Пусть F P i Q j R k .

Тогда

f F f P i f Q j f R k

779

и

div f F f P x f Q y f R z

fx P f Px f y Q f Qy fz R f Rz

fx P f y Q fz R f Px Qy Rz .

В первой скобке стоит скалярное произведение градиента скалярного поля f на вектор F, а во второй – дивергенция векторного поля F. Таким обра-

зом, div f F grad f F f div F .

Дивергенция – это локальная характеристика векторного поля. Она характеризует свойства поля в точках и бесконечно малых окрестностях, прилегающих к этим точкам.

6.3.5. Теорема Остроградского-Гаусса

Существует ряд интегральных теорем, описывающих свойства векторного поля в целом. Одной из них является теорема Остроградского-Гаусса.

Рассмотрим физический смысл этой теоремы. Пусть в области D задано векторное поле F P(x, y, z), Q(x, y, z), R(x, y, z) .

Теорема Остроградского-Гаусса утверждает, что величина потока векторного поля изнутри любой замкнутой поверхности q D равна суммарной

мощности источников поля, заключенных внутри этой поверхности, т. е.

где V – область, ограниченная поверхностью q .

Равенство (6.3.6) является векторной формой теоремы ОстроградскогоГаусса.

Заменим дивергенцию, стоящую под знаком тройного интеграла, ее выражением через частные производные по формуле (6.3.5), а скалярное

произведение F,n0 запишем через координаты векторов F и n0 . Тогда равенство (6.3.6) примет вид

где cos cos(n, x) , cos cos(n, y) , cos cos(n, z) .

Это выражение называют теоремой (формулой) Остроградского-Гаусса в координатной форме. Сама теорема формулируется следующим образом:

Теорема 1 (Остроградского-Гаусса). Интеграл от дивергенции век-

торного поля F по объему равен потоку вектора через поверхность, ограниченную этим объемом.

780

Теорема Остроградского-Гаусса дает еще один способ вычисления потока векторного поля через замкнутую поверхность путем сведения его к тройному интегралу по области V , заключенной внутри поверхности.

Пример 8. Найти поток векторного поля F(x 1, y 3, z) через боковую поверхность конуса z2 x2 y2 , заключенную между плоскостями z 0 и

z 1 в направлении внешней нормали.

Решение. Рассмотрим тело V , границей которого служит коническая

q q1 q2 , являющейся объединением поверхностей q1 и q2 , возьмем внешнюю нормаль n . Поток П через поверхность q складывается из потоков П1 и П2 через поверхности q1 и q2 соответственно. Следовательно, интересующий нас поток может быть найден как разность потоков: П1 =П–П2 . Поток П может быть найден по формуле Остроградского-Гаусса:

П F n d divFdV 3 dV .

Последний интеграл представляет собой объем тела V . Тело представляет собой конус с высотой h 1 и радиусом основания R 1. По известной

из элементарной математики формуле, его объем равен 13 R2h 13 . Отсюда

П2 F nd z d .

q2 q2

Поскольку z 1 на q2 , а элемент площади ( d ) равен элементу площади ее проекции на плоскость xOy ( dxdy ), то последний интеграл сводится к

двойному:

dxdy ,

Dxy

где Dxy – круг с центром в начале координат и радиуса 1. Этот интеграл

выражает площадь этого круга, которая равна . Следовательно, искомый поток через коническую поверхность равен П1 =П–П2 = - =0.

Пример 9. Вычислить поверхностный интеграл

zdxdy,

q

где q – внешняя сторона эллипсоида

x2 y2 z2 1. a2 b2 c2