4. Принцип достоверности содержания практических приложений математики.

Этот принцип означает необходимость достоверного отражения реальных объектов в сюжетах задач и прикладных иллюстраций. Отобранные для обучения практические приложения математики должны демонстрировать школьникам действенность математических методов для изучения процессов и явлений действительного мира. В практике обучения описание реальных объектов из-за их сложности и многоаспектности часто возможно дать только в упрощенном, «очищенном» виде. Однако недопустимо выхолащивание сути описываемой реальной ситуации и использование ее только в дидактических целях. Это искажает представления школьников об изучении реальности с помощью математики, делает их недостаточно достоверными.

5. Принцип открытости содержания линии ППМ.

Принцип означает, что обеспечивающие реализацию линии ППМ наборы задач, исследовательские и проектные задания, методические разработки элективных и курсов по выбору допускают возможность их дополнения образовательными продуктами, созданными учителем.

Тема 4. Цели, задачи и этапы реализации линии ППМ

Уровни обучения математическому моделированию по Н.Я. Виленкину, этапы процесса математического моделирования (математизация, формализация, внутримодельное решение, интерпретация результата), этапы реализации линии ППМ (пропедевтический, подготовительный, основной, заключительный). уровни сложности задач на приложения математики, прикладные математические умения школьников, компоненты линии ППМ (содержательный, деятельностный, задачно-классификационный; процессуальный)

Сформулированные ранее принципы конструирования линии ППМ определяют цели, задачи и этапы ее реализации.

Так как базовым понятием линии ППМ является понятие

77

математической модели, а математическим методом – метод математического моделирования, то прежде чем перейти к рассмотрению целей, задач и этапов реализации этой линии, представим наше понимание последовательности изучения школьниками элементов метода математического моделирования. Использованию элементов метода математического моделирования в школе посвящено немало методических исследований, в большинстве из которых выделялись различные этапы и уровни обучения этому методу. Н.Я. Виленкиным95 выделены «в порядке нарастающей сложности» следующие уровни обучения математическому моделированию, определяющие последовательность изучения понятий, связанных с этим методом. Приведем их. Это обучение:

1)«языку», на котором будет вестись моделирование;

2)«переводу» реальной ситуации на данный математический язык;

3)выбору существенных переменных и построение схемы их взаимосвязей;

4)составлению математических выражений реально существующих отношений и связей;

5)решению математически выраженных отношений и связей, истолкованию полученного ответа;

6)исследованию полученного решения, и, в частности, простейшим навыкам самоконтроля.

Содержание этих уровней обосновывает необходимость и целесообразность выделения четырех этапов процесса математического моделирования в обучении математике в школе: математизация (анализ условия), формализация (построение математической модели условия), внутримодельное решение, интерпретация результата. Чаще выделяют только три этапа: формализация (построение математической модели); внутримодельное решение; интерпретация результата. Но при решении ряда задач не всегда возможно сразу предъявить математическую модель

95 О путях совершенствования содержания и преподавания школьного курса математики / Р.К. Таварткиладзе, Н.Я. Виленкин. - Тбилиси: Изд-во Тбил. ун-та, 1985. - 356 с.

78

условия. Например, в фабуле задачи присутствует непонятная или неизвестная учащимся нематематическая терминология. Поэтому целесообразно выделить еще один этап – этап математизации, на котором будет проделана подготовительная работа к составлению математической модели: проведен предварительный анализ условия задачи с целью установления возможности применения математики для ее решения, определены все нематематические термины, дана им математическая интерпретация, выявлены отношения между объектами условия задачи, уяснен смысл задачи в целом.

Итак, в качестве этапов процесса математического моделирования выделим следующие:

0 этап. Математизация (анализ условия).

1 этап. Формализация (построение математической модели условия).

2 этап. Внутримодельное решение.

3 этап. Интерпретация результата.

Учитывая необходимость обучения школьников элементам метода математического моделирования, руководствуясь представленными в нормативных документах требованиями к уровню геометрической подготовки учащихся по использованию приобретенных знаний и умений

впрактической деятельности и повседневной жизни, а также опираясь на принципы конструирования линии практических приложений математики

вшколе, сформулируем общие цели ее реализации:

1.Формирование системы математических знаний во взаимосвязи с их практическими приложениями к изучению окружающего мира.

2.Формирование прикладной математической грамотности, понимаемой как способность использовать математику для описания действительности и решения задач реального мира методом математического моделирования.

3.Демонстрация идей математизации наук через знакомство с

79

теоретическими основами практических приложений математики. Перечисленные цели достаточно широки и могут быть достигнуты

на двух уровнях – прагматическом и исследовательском. Начальный уровень, прагматический, определяется необходимостью ориентации в современном мире для практической жизни, подготовленностью к решению бытовых и профессиональных задач с использованием математического аппарата. Этот уровень посилен для всех учащихся и заложен в стандартах общего математического образования. Продвинутый уровень, исследовательский, состоит в наличии способности обучаемого математически исследовать объекты реального мира с различными целями, т.е. в математическом подходе к явлениям реального мира96. Достижение этого уровня доступно не всем учащимся. Обучение на таком уровне возможно организовать во внеклассной работе по математике: на занятиях курсов по выбору и элективных курсов, при выполнении школьниками исследовательских и проектных заданий и т.п.

Выделение ведущей идеи реализации линии ППМ позволило перейти к конкретизации этой идеи в виде принципов конструирования и следующих из них общих целей реализации линии. Так, например, принцип математизации знаний с одной стороны следует из указанной в ведущей идее необходимости формирования у школьников понимания роли математики в изучении реального мира, а с другой стороны лежит в основе всех трех целей реализации линии ППМ.

Этапы реализации линии ППМ.

Выделим четыре этапа реализации линии практических приложений математики в школе: пропедевтический, подготовительный, основной и заключительный. Они вполне традиционны. Укажем временные рамки для этих этапов:

1.Пропедевтический (основная ступень, 5–6 класс)

2.Подготовительный (основная ступень, 7 класс)

96 Арнольд В.И. Математика и математическое образование в современном мире. В сб. Математика в образовании и воспитании. Сост. В.Б. Филиппов. - М.: Фазис, 2000. - 256 с.

80

3.Основной (основная ступень, 8–9 класс)

4.Заключительный (старшая ступень, 10–11 класс) Пропедевтический этап достаточно хорошо изучен и реализован в

УМК для 5-6 классов разных авторов. Например, в учебниках математики Н.С. Подходовой и др., а также Л.Г. Петерсон, Т.Г. Ходот, И.И. Зубаревой и А.Г. Мордковича отражена работа с учащимися по формированию интуитивных представлений о модели, математической модели, процессе моделирования.

Так, в учебнике математики для 5 класса И.И. Зубаревой и А.Г. Мордковича97 изучаются темы «Математический язык», «Математическая модель». Понятие модели вводится с помощью рассмотрения двух задач, в которых требуется найти значение одного и того же выражения. Выражение, полученное в процессе решения, согласно авторам, - это математическая модель реальной жизненной ситуации, о которой говорится в задаче. Авторы обращают внимание учащихся на следующее: «Выполняя задания по переводу «обычной» речи на математический язык, мы каждый раз составляли математическую модель данной ситуации. Однако важно не только уметь составлять математические модели, но и выполнять обратную работу – понимать, какую ситуацию (или обстоятельства) описывает данная модель». Таким способом неявно выделяются этапы моделирования: формализация и интерпретация.

Учащиеся приобретают простейшие навыки работы с моделями на примере решения текстовых задач, сопоставления реальных объектов с их математическими прообразами. Таким образом, считаем, что выделен и разработан пропедевтический этап линии практических приложений математики в школе. Рассмотрим остальные три этапа реализации линии ППМ – подготовительный, основной и заключительный для школьного курса геометрии.

97 Зубарева И.И. Математика. 5 кл.: Учебник для общеобразоват. Учреждений / И.И. Зубарева, А.Г. Мордкович. - 2-е изд. - М.: Мнемозина, 2003. -293 с.

81

Частные образовательные задачи реализации линии ППМ. Для каждого этапа на основании указанных общих целей сформулированы

частные образовательные задачи реализации линии ППМ с учетом содержания курса геометрии в заданный временной отрезок; закономерностями окружающего мира, понятными школьникам в связи с изучением нематематических дисциплин и приобретением жизненного опыта; степенью овладения приемами мыслительной деятельности (синтезирование, анализирование, установление аналогий и т.д.) и учебнопознавательной деятельности школьников; последовательностью изучения элементов метода математического моделирования. Перейдем к рассмотрению частных задач подготовительного, основного и заключительного этапов реализации линии ППМ.

2. Подготовительный этап (основная ступень, 7 класс)

К седьмому классу у школьников происходит расширение знаний о мире. Количество учебных предметов, изучаемых ими увеличивается: математика делится на две дисциплины (алгебра и геометрия), начинается изучение физики, продолжается изучение биологии и географии. Значит, появляется возможность использовать содержательные примеры приложений геометрии к естествознанию. К этому возрасту у учащихся накоплен определенный практический опыт и в повседневной жизни.

С позиций возрастной психологии в возрасте 12–13 лет активно формируется продуктивное представление, (понимаемое А.А. Реаном98 как воспроизведение образов предметов, не воспринимаемых в данный момент времени, в контексте новых условий и с учетом всех основных свойств этих предметов), а также произвольное внимание (по Л.С. Выготскому, один из видов внимания – психический процесс, который заключается в сознательном и активном сосредоточении субъекта в данный момент времени на каком-либо реальном или идеальном объекте). К этому возрасту также начинает преобладать словесно-логическое, абстрактное

98 Психология человека от рождения до смерти / Под общей редакцией А.А. Реана. - СПб.: ПРАЙМ-ЕВРОЗНАК, 2002. - 683 с.

82

мышление. Эти особенности личности школьников позволяют осуществить подготовительный этап реализации линии ППМ.

На подготовительном этапе ставятся следующие частные

образовательные задачи:

создать мотивацию изучения геометрии во взаимосвязи с ее практическими приложениями к изучению окружающего мира;

ввести понятие математической модели на геометрическом

материале;

сформировать представление об этапах метода математического моделирования при решении задач, связанных с приложениями геометрии;

нацелить учащихся на выявление возможностей применения математического аппарата при изучении естественного блока школьных дисциплин.

На этом этапе предполагается развить понятие математической модели, сформированное у школьников на интуитивном уровне на пропедевтическом этапе. В учебнике алгебры 7 класса автора А.Г. Мордковича99 это понятие вводится на примере решения текстовой задачи следующего содержания: «В школе четыре седьмых класса. В 7А учатся 15 девочек и 13 мальчиков, в 7Б — 12 девочек и 12 мальчиков, в 7В — 9 девочек и 18 мальчиков, в 7Г — 20 девочек и 10 мальчиков. Если нам нужно ответить на вопрос, сколько учеников в каждом из седьмых классов, то нам 4 раза придется осуществлять одну и ту же операцию сложения:

После ее решения автор указывает: «Используя математический язык, можно все эти четыре разные ситуации объединить: в классе учатся а девочек и b мальчиков, значит, всего учеников а+b. Такова математическая модель данной реальной ситуации. Алгебра, в частности,

99 Мордкович А.Г. Алгебра. 7 кл.: В двух частях. Ч.1 Учебник для общеобразоват. учреждений. 13-е изд. испр. - М.: Мнемозина, 2009. - 160с.

83

занимается тем, что описывает различные реальные ситуации на математическом языке в виде математических моделей, а затем имеет дело уже не с реальными ситуациями, а с этими моделями, используя разные правила, свойства, законы, выработанные в алгебре».

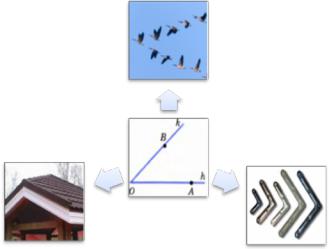
Такой путь введения понятия математической модели есть необходимость повторить на уроках геометрии в 7 классе для обобщения этого понятия. Например, при изучении начальных геометрических понятий предлагаем использовать следующую схему «Угол» (рис. 1), центральным элементом которой является математическая (геометрическая) модель реального объекта, выраженная словесно и (или) графически. Далее учитель дает учащимся такое уточнение этого понятия:

Математическую модель, отображающую геометрические свойства объекта, называют геометрической моделью.

Рис. 1

Аналогичным образом (на примере решения текстовой задачи) в курсе алгебры вводится трехэтапная схема применения метода математического моделирования: «первый этап – составление математической модели, второй этап – работа с математической моделью,

84

третий этап – ответ на вопрос задачи».100 Такая работа проводится в самом начале изучения курса алгебры.

На первых уроках геометрии в 7 классе при изучении основных свойств измерения углов есть возможность показать применение метода математического моделирования по четырем этапам, например, при решении следующей задачи:

 Наблюдая на пристани за отплывающим кораблем можно заметить, что по мере удаления от берега его видимый размер уменьшается. Как объяснить это явление?

Приведем пример поиска решения задачи согласно выделенным этапам, который учащиеся осуществляют вместе с учителем. Предварительно сделаем следующее замечание. Рассмотренные общий подход к построению математической модели реального объекта в прикладной математике (А.Д. Мышкис, А.Н. Тихонов, Г.И. Рузавин), методические исследования по использованию математического моделирования в обучении математике (А.Я. Блох, А.Г. Мордкович, В.А. Стукалов) показывают, что процесс математизации реального объекта, т.е. перевод условия задачи на математический язык, определяет выбор математического аппарата для решения задачи. Для того чтобы этот выбор был сделан в соответствии с реальной ситуацией задачи, предлагаем этап математизации проводить по следующему плану:

1.Уяснение смысла нематематических понятий, входящих в условие

задачи.

2.Выделение реальных объектов, значимых для решения задачи. Установление связей между этими объектами.

3.Подбор математических интерпретаций, адекватных выделенным реальным объектам.

0 этап. Математизация.

1.Уяснение смысла нематематических понятий, входящих в условие

100 Мордкович А.Г. Алгебра. 7 кл.: В двух частях. Ч.1 Учебник для общеобразоват. учреждений. 13-е изд. испр. - М.: Мнемозина, 2009. - 160с.

85

задачи.

Начнем с пояснения, что означают слова «видимый размер». В противном случае не понятно, что за явление надо объяснить. Мы хорошо знакомы с линейными размерами предметов. Сколько их? Как их принято называть?

(Ответ: три размера – длина, ширина и высота.)

При описании свойств математических объектов встречается понятие видимого размера. Часто оно используется в упрощенном виде. Мы говорим, например: «Из точки А отрезок а виден под углом » Такой угол принято называть видимым или угловым размером предмета.

Понятие углового размера очень важно в астрономии. Знание углового размера (астрономы говорят углового диаметра или видимого диаметра) небесного тела позволяет вычислить его линейные размеры. Угловых размеров у предмета может быть бесконечно много, так как имеется бесчисленное число точек наблюдения – вершин углов зрения, под которыми виден предмет. Иначе говоря, угловой размер предмета зависит от выбранной точки наблюдения. Для решения практических задач выбирают «удобный» угол зрения, например, тот, под которым видна высота рассматриваемого предмета.

2.Выделение реальных объектов, значимых для решения задачи. Установление связей между этими объектами.

Теперь выделим объекты условия задачи: наблюдатель, корабль, расстояние от берега до корабля. Они все связаны между собой. Есть еще объекты (берег, пристань), которые не влияют на поиск решения задачи. Но на первоначальном рисунке мы их изобразим. (Возможно предложить школьникам и готовый рисунок к условию).

3.Подбор математических интерпретаций, адекватных выделенным реальным объектам.

86

По этому рисунку сделаем чертеж, отбирая нужные объекты и устанавливая к ним подходящие геометрические эквиваленты (рис. 2). Изобразим на одном чертеже два положения корабля по мере удаления от берега. Точкой О обозначим наблюдателя (точнее его глаз), отрезки АВ и А1В1 – корабль (или его высота над поверхностью воды), отрезки ОА и ОА1 (ОА< ОА1) - расстояние от наблюдателя до корабля.

В этом примере этап математизации описан достаточно подробно. Его изложение может быть сокращено с учетом уровня математической подготовки школьников, их интересов, жизненного опыта и наличия учебного времени. Однако план реализации этого этапа необходимо довести до сведения учащихся.

1 этап. Формализация. Построенный чертеж и есть геометрическая модель условия задачи. Однако не хватает вопроса задачи. Сформулируем задачу так: луч ОВ1 проходит между сторонами угла АОВ. Какой угол больше: АОВ или А1ОВ1? Почему? В приведенной формулировке задача встречается в учебнике автора Погорелова А.В.101

2 этап. Внутримодельное решение. Так как на рис. 2 луч ОВ1 проходит между сторонами угла АОВ и пересекает отрезок АВ с концами на его сторонах, то по свойству измерения углов (градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами) АОВ>А1ОВ1.

3 этап. Интерпретация. Так как угол, под которым виден корабль с увеличением расстояния уменьшается, тот и его видимые размеры уменьшаются.

101 Погорелов А.В. Геометрия: Учеб. пособие для 6-10 кл. сред. шк. 6-е изд. - М.: Просвещение, 1987. С.19, зад. 29.

87

обучению этапу математизации, его выполнение является наиболее сложным. Содержание этого этапа также нацеливает учащихся на применение математики при изучении физики.

При решении ряда задач на приложения математики в школе ситуация, описанная в условии, практически не нуждается в математизации, т.е. проведение нулевого этапа не требуется. Например, рассмотрим следующую задачу, при решении которой воспользуемся трехэтапной схемой применения метода математического моделирования (этапы 1–3). Здесь, в отличие от предыдущей задачи, не требуется выделять математизируемые объекты, устанавливать их свойства и отношения между ними. Этот процесс очевиден, поэтому сразу переходим

кпервому этапу – построению математической модели условия задачи.

От оконного стекла треугольной формы откололся один из его уголков. Можно ли по сохранившейся части вырезать такое же оконное стекло?

1 этап. Изобразив стекло на рис. 3 согласно описанной ситуации, приходим к математической формулировке задачи:

Имеется треугольник, у которого известны сторона и прилежащие к ней углы. Можно ли построить треугольник равный данному?

88

модель исходной задачи.

2 этап. Внутримодельное решение сводится к обоснованию возможности построения треугольника по трем заданным элементам на основании соответствующего признака равенства треугольников.

3 этап. Для того чтобы заказать стекло необходимо измерить сохранившуюся сторону и углы.

На примере этой задачи учитель может показать учащимся важность этапа интерпретации для практической деятельности и таким образом способствовать формированию их познавательного интереса, а значит, и мотивировать изучение геометрии.

Таким образом, на подготовительном этапе учителю необходимо ввести понятия «математическая модель» и «метод математического моделирования» на геометрическом и на алгебраическом материале. Такой подход способствует формированию у школьников наиболее полных представлений об этих центральных для рассматриваемой линии понятий. Приведенные примеры демонстрируют возможность выполнения задач первого, подготовительного, этапа реализации линии практических приложений математики в школе.

3. Основной этап (8–9 класс)

Содержанием этого этапа является накопление знаний о практических приложениях геометрии и приобретение учащимися опыта применения метода математического моделирования к решению задач.

На основном этапе решаются следующие частные образовательные задачи, развивающие задачи предыдущего этапа:

поддерживать мотивацию изучения геометрии во взаимосвязи

сее практическими приложениями к окружающему миру;

расширить представление об этапах метода математического моделирования при решении задач, связанных с приложениями геометрии (выделять этапы решения задачи на приложения, строить математическую модель по содержательной модели согласно заданной цели, выбирать

89

рациональный метод решения задачи, интерпретировать полученный результат);

 формировать умение выделять математический аппарат, используемый при описании реальных объектов в учебной и научнопопулярной литературе. (Здесь имеется в виду процесс взаимодействия личности с математическим знанием. Научить всем «рецептам» решения задач невозможно. Необходимо формировать у ученика способность понимать смысл поставленной перед ним задачи, а затем обучать поиску математических методов (или к.-л. других методов), адекватных поставленной проблеме.)

На этом этапе продолжается обучение школьников построению математических моделей, адекватных предложенной задачной ситуации. Школьникам предлагаются для решения задачи на приложения, математическая модель которых может быть выбрана несколькими способами или с различной степенью точности и т.п.

Рассматривая специально подобранный пример (или серию примеров), учащиеся убеждаются, что математическая модель – это приближенное описание какого-либо класса объектов102 реального мира на языке математики, при этом один объект может иметь более одной модели. Геометрическая модель описывает геометрические свойства объекта согласно заданной цели.

В 8–9 классах обращается специальное внимание учащихся на особенности работы с моделью на каждом этапе. С этой целью подбираются примеры задач, имеющие несколько внутримодельных решений. Так, в зависимости от требований условия, должна вестись работа по выбору рационального решения. Для иллюстрации особенностей такой работы подбираются задачи, в которых интерпретация ответа нетривиальна – учащимся необходимо выбрать необходимую точность числа, форму его представления и т.п. Также на этом этапе учитель обращает внимание учащихся на то, что одна математическая модель

102 Здесь термин объект понимается в наиболее широком смысле: объектом может служить не только то, что обычно именуется этим словом, но и любая ситуация, явление, процесс и т. д

90

может быть использована для интерпретации различных по своей природе объектов.

4. Заключительный этап (10–11 класс)

На этом этапе происходит обобщение сведений, полученных о практических приложениях школьного курса геометрии. Такое обобщение производится по направлениям приложений: приложения геометрии к естествознанию (физика, химия, биология, астрономия); приложения геометрии к практическим дисциплинам (строительство, архитектура, геодезия и т.п.); приложения геометрии к изобразительному искусству (живопись, фотоискусство, скульптура) и т.д., а также по теоретическим основам приложений (сферическая геометрия как основа геодезии, астрономии и картографии; теория математических бильярдов, применяемая для изучения динамики твердого тела). Такая методическая работа ведется с учетом профиля обучения на старшей ступени общего образования.

Представленный подход согласуется с особенностями данного возрастного периода. Старшеклассники оценивают учебный процесс с позиции своей будущей профессиональной деятельности. Характерной особенностью учебно-познавательной деятельности старшеклассника является ее активизация и возрастающая самостоятельность. Мышление учащихся этого возраста приобретает творческий характер, повышается их способность к абстрагированию и обобщению изученного. В этот период активно формируется научное мировоззрение и теоретическое мышление, направленное на познание общих закономерностей окружающего мира.103 В связи с этим, на уроках и элективных курсах необходимо обратить внимание школьников на теоретические основы приложений, связанные с такими темами как «Основы сферической геометрии», «Элементы начертательной геометрии», «Теория математических бильярдов» и т.д.

Заключительный этап предполагает решение следующих частных

103 Смирнова И.М. Педагогика геометрии: Монография. - М.: Прометей, 2004.- 336 с.

91

образовательных задач, которые развивают задачи предыдущих этапов:

обобщить и систематизировать знания учащихся по геометрии как теоретической основы приложений;

показать возможности использования метода математического моделирования для решения широкого круга задач, связанных с практическими приложениями геометрии, в том числе требующих всестороннего анализа данных и допускающих неоднозначное построение математической модели;

достичь овладения учащимися следующими элементами метода математического моделирования: осуществление анализа содержания задачи, направленного на выявление объектов, подлежащих математизации, установление соответствия между содержательной и математической моделью объекта;

способствовать формированию прикладной исследовательской деятельности при изучении теоретических основ приложений, которые выходят за рамки школьного курса геометрии.

Сложность поиска решения задач этого типа, прежде всего, связана с осуществлением нулевого этапа метода математического моделирования – этапа математизации. Частные задачи всех трех этапов реализации линии сформулированы с учетом необходимости обучения школьников математизации реальных объектов. В связи с этим выделим уровни сложности выполнения этапа математизации при решении задачи на приложения математики, которые и будем считать уровнями сложности таких задач. Таких уровней четыре:

I. В задаче имеется прямое указание на математическую модель.

II. Прямого указания на модель нет, но объекты и отношения задачи легко соотносимы с соответствующими математическими объектами и отношениями.

III. Объекты и отношения задачи соотносимы с математическими объектами и отношениями, но неоднозначно. Требуется учет реально

92

сложившихся условий.

IV. Объекты и отношения задачи явно не выделены или их математические эквиваленты неизвестны школьникам.

Задачи первых двух уровней сложности, как правило, не вызывают у школьников затруднений при построении математической модели и готовят к решению задач третьего уровня. Одна из особенностей задач третьего уровня состоит не только в нетривиальности построения математической модели, но и в неопределенности выбора математического аппарата для их решения. Это сближает такие задачи с прикладными задачами, поставленными в реальной ситуации.

Задачи первых двух уровней целесообразно использовать на уроках математики. Задачи третьего и четвертого уровней требуют большего учебного времени для решения, поэтому их предпочтительнее использовать во внеклассном обучении математике. Задачи третьего и четвертого уровня сложности в большинстве составляют задачи, направленные на развитие умения применять метод математического моделирования для решения широкого круга задач, связанных с практическими приложениями геометрии, в том числе требующих всестороннего анализа данных и допускающих неоднозначное построение математической модели. К ним могут быть отнесены задачи с недостающими, лишними, противоречивыми и скрытыми данными. Рассмотрим эти уровни подробнее.

I. В задаче имеется прямое указание на математическую модель.

На первом уровне рассматриваются такие содержательные модели реальности, объекты и отношения которых практически не требуют математизации. Математическая модель представлена в явном виде. Например, такова следующая задача:

 Для определения того, что керамическая плитка имеет квадратную форму, измеряют и сравнивают ее диагонали. Достаточна ли такая проверка?

93

При переводе на математический язык, получаем такую задачу:

 Верно ли, что если диагонали прямоугольника равны, то этот прямоугольник – квадрат?

94

Также примером задач этого уровня служат задачи на использование различных инструментов для проведения измерений. В содержательной модели таких задач имеется прямое указание на математическую модель. Для их решения необходимо только найти подходящий математически аппарат, т.е. выполнить внутримодельное решение. Этап интерпретации здесь отсутствует.

Можно ли пользоваться чертежным угольником как центроискателем? Каким образом?

Если под рукой не оказалось чертежного угольника, то прямой угол можно получить двукратным перегибанием листа бумаги любой формы. Объясните, почему в данном случае получаются прямые углы?

II. Объекты и отношения задачи легко соотносимы с соответствующими математическими объектами и отношениями.

На втором уровне объекты и отношения задачи хорошо знакомы учащимся из жизненного опыта или в результате изучения других школьных дисциплин. Поэтому школьники могут легко соотнести их с соответствующими математическими объектами и отношениями. Это наиболее многочисленная группа задач. Большинство задач этой группы составляют задачи, назначение в обучении которых связано с

формированием математических понятий.

Приведем содержательную модель такой задачи, которая может стать основой для нескольких задач:

Лестница прислонена к стене дома.

Составим следующий набор задач по этой содержательной модели:

На какую высоту можно подняться по лестнице длиной L, отстоящей от стены на расстояние b.

Какой длины должна быть лестница, чтобы по ней можно было взбираться на высоту h? Ее нижний конец при этом отстоит от стены на расстояние b.

95

Фонарь висит на стене дома на высоте h. Можно ли в нем заменить лампочку, воспользовавшись лестницей длины L. Лестница не съезжает со стены, если прислонена к ней под углом α.

У этих задач одна математическая модель – прямоугольный треугольник, но для их внутримодельного решения используется разный математический аппарат: для первых двух задач - теорема Пифагора, для последней – определение косинуса угла в прямоугольном треугольнике. Таким образом, подобный набор задач позволяет во взаимосвязи формировать ряд понятий, объединённых понятием прямоугольного треугольника.

В условии следующей задачи уже сделаны необходимые упрощения. Все объекты задачи имеют математические эквиваленты, поэтому составление математической модели такой задачи, как правило, не вызывает затруднений у школьников.

 Человек среднего роста на совершенно ровном месте видит вокруг себя не далее 4,5 км. Как велика в градусной мере, та дуга земной поверхности, которую он видит? Радиус Земли принять равным 6400км.

математическими объектами и отношениями неоднозначно. Требуется учет реально сложившихся условий.

На третьем уровне объекты и отношения содержательной модели неоднозначно соотносимы с их математическими эквивалентами. Соответствующая математическая модель выбирается в зависимости от реальных условий, описанных в задаче.

Например, на карте Московской области Москва и другие города занимают определенную площадь, а, значит, их математической моделью может служить некоторая геометрическая фигура. Но на политической карте Европы столицы государств, в том числе и Москва, отмечены небольшими кружочками. В этом случае математическая модель города – точка, которая, как известно, не имеет размеров.

96

В следующих примерах построение математической модели усложнено тем, что в условии задачи есть объекты, математические интерпретации которых также неоднозначны.

Найдите расстояние между двумя соседними меридианами на

экваторе.

Если принять, что Земля имеет форму геоида, то такая модель Земли не позволит решить задачу средствами школьного курса геометрии. Если моделью формы Земли будет сфера, тогда для решения задачи будет использована известная школьникам формула длины дуги окружности.

На какой широте Земли длина параллели в два раза меньше, чем длина экватора?

Казалось бы, понятия широта, параллель, экватор хорошо знакомы учащимся. Эти понятия изучаются в курсе географии 6 класса.104 Однако понятие широты может быть определено по-разному. Часто встречается такое определение:

Географической широтой заданной точки называется величина в градусах дуги меридиана от экватора до параллели, проходящей через эту точку.

Приведенное определение является, по сути, наглядной иллюстрацией широты на глобусе, который, как известно, имеет форму шара. Если принять, что Земля – геоид, то строгое определение широты таково:

Географическая широта точки М это величина угла м между отвесной линией в данной точке и плоскостью экватора, отсчитываемый от 0 до 90° в обе стороны от экватора, причем к северу от экватора широта

считается положительной, а к югу – отрицательной, -900 м 900. Значит, при поиске математического эквивалента понятия широты,

учащиеся могут встретить два приведенных выше определения. Школьникам необходимо выбрать, каким из них целесообразно

104 Герасимова Т.П., Неклюкова Н.П. Начальный курс географии. 6 класс. - М.: Дрофа, 2010. - 176 с.

97

воспользоваться при решении данной задачи.

Приведем пример задачи, в которой выбор подходящего математического аппарата для внутримодельного решения зависит от конкретных условий, имеющих место в реальности.

На плоскости обозначены три точки А, В, С, не лежащие на одной прямой. Через точку А проложите прямую, параллельную ВС.

Эта задача имеет несколько решений. Выбор подходящего математического аппарата для внутримодельного решения зависит от условий, которые могут появиться в реальной ситуации прокладывания этой параллельной прямой. Например, если необходимо построить забор, параллельно имеющемуся, то возможно предположить, что для построений на местности мы будем ограничены шириной улицы. Также ограничения могут возникнуть со стороны возможности использования геодезических инструментов. Если построения проводятся не на местности, а, например,

вплотницком деле для разметки деревянных деталей, то и математическая модель будет соответствовать этим реальным условиям.

IV. Объекты и отношения задачи явно не выделены или их математические эквиваленты неизвестны школьникам.

На четвертом уровне объекты и отношения, подлежащие математизации, в содержательной модели не выделены. Проиллюстрируем это на примере следующей задачи:

Определите, на какой табурет (рис.4 а, б) можно сесть без риска оказаться на полу?

98

Рис.4а Рис.4б

Втексте задачи речь идет о табурете, а объектами, которые необходимо математизировать, являются его ножки и сидение, точнее их взаимное расположение. Математическими эквивалентами этих объектов являются отрезки, которые на рис. 5б образовывают треугольник. Т.к. эта фигура является жесткой, то именно на такой табурет можно садиться. Ясно, что, пользуясь жизненным опытом, школьники могут указать правильное решение. Однако просьба воспроизвести необходимые математические рассуждения вызывает затруднения даже у студентов старших курсов математического факультета МПГУ.

Вследующей задаче требуется выделить нужные характеристики объекта и учесть их при ее решении.

 В магазине имеются чайники четырех моделей. Выберите тот чайник, в котором вода будет остывать дольше всего.

При такой формулировке задачи учащиеся исследуют вопросы об объеме чайников и материале, из которого они изготовлены. Если эти параметры совпадают, то решение задачи сводится к сравнению их площадей поверхностей.

К этому уровню также относим задачи, в содержании которых встречается непонятная или неизвестная школьникам терминология. Например, для решения следующей задачи учащимся необходимо вспомнить или изучить заново понятия «курс корабля» и «ортодромия», «географические координаты точки».

 Вычислить начальный курс корабля при движении по ортодромии из А в В, если известны географические координаты этих

точек А, А и В, В.

Определение уровня сложности задачи на приложения в практической работе учителя целесообразно проводить по двум критериям: новизна для школьников объектов и отношений содержательной модели задачи; сложность подбора математических

99

эквивалентов к этим объектам и отношениям.

Выбор этих критериев обоснован тем, что у учащихся имеется некоторая сумма знаний и жизненный опыт, соответствующие их возрасту и содержанию школьной программы. Так, поиск решения задачи о табуретах у учащихся старшего школьного возраста не вызовет затруднений. Ими уже накоплены для этого необходимые предметные знания и жизненный опыт. Поэтому для них эта задача не будет задачей высокого уровня сложности. Следовательно, уровень сложности задачи на приложения – характеристика непостоянная. Так, одной и той же задаче, решенной, например, в 7 классе на уроке и в 9 классе на итоговой аттестации, может быть присвоен разный уровень сложности. Это может быть связано, например, с изменением оценивания первого критерия (степени новизны для школьников объектов и отношений содержательной модели) за время обучения. Определение уровней сложности задач на приложения позволит выделить базовые задачи, решение которых является обязательным для всех учащихся заданной возрастной группы.

Таким образом, на подготовительном этапе реализации линии практических приложений школьного курса математике обучение математизации целесообразно использовать задачи первого и второго уровня сложности, на основном этапе - задачи с первого по третий уровень сложности, заключительный этап характеризуется присоединением задач четвертого уровня к первым трем.

В процессе обучения практическим приложениям математики в школе необходимо формировать у учащихся прикладные математические умения. Систематизируем их по четырем этапам метода математического моделирования. Учащиеся должны уметь:

0 этап. Математизация (анализ условия).

0.1.Выделять объекты окружающей действительности, которые могут быть описаны средствами школьного курса математики.

0.2.Заменять исходные объекты и отношения их математическими

100

эквивалентами. Описывать эти объекты и отношения на языке математики.

1 этап. Формализация (построение математической модели условия).

1.1.Устанавливать соответствие между содержательной и математической моделью объекта в зависимости от предъявленных условий.

1.2.Соотносить реальные объекты различной природы с одной математической (геометрической) моделью.

1.3.Описывать реальный объект несколькими математическими (геометрическими) моделями.

1.4.Оценивать полноту исходных данных для построения математической модели.

2 этап. Внутримодельное решение.

2.1.Выбирать рациональные методы исследования реальных объектов в зависимости от поставленной задачи.

2.2.Составлять математическую модель с учетом требуемой точности описания реальных объектов задачи.

3 этап. Интерпретация результата.

3.1.Анализировать использованные математические методы решения

сточки зрения их рациональности для исследования реального объекта.

3.2.Интерпретировать результат исследования математической модели с требуемой погрешностью.

Представим структуру линии ППМ, выделив следующие ее компоненты: содержательный, включающий содержание учебного материала, базовое понятие, этапы процесса математического моделирования; деятельностный, представленный прикладными математическими умениями школьников; задачно-классификационный содержащий систему классификаций задач на приложения (она будет представлена далее) и характеристику уровней их сложности; процессуальный, в котором выделены временные этапы реализации линии.

101

На рис. 5 представлена описанная структура линии ППМ, иллюстрирующая взаимосвязи и соподчиненность перечисленных компонентов (на схеме это отражено соответственно дву- и однонаправленными стрелками). Так, из анализа содержания учебного материала линии ППМ, следует, что ее базовым понятием является понятие математической модели, а основным методом – метод математического моделирования, этапы которого определяют прикладные математические умения школьников. Это в свою очередь позволило выделить уровни сложности задач на приложения и установить их связи с этапами реализации линии ППМ.

На основе приведенной систематизации прикладных математических умений, выделим типы заданий, способствующих их формированию.

1.Сформулировать математические утверждения, отобрать формулы, понятия, которые необходимо использовать для ответа на вопрос задачи (здесь и далее имеется в виду задача на приложения).

2.Выбрать из предложенных задачу, в которой математической моделью является следующее утверждение, понятие, формула.

3.Среди данных задач найти такие, у которых математические модели совпадают.

4.Указать математические модели следующих реальных объектов (у одного объекта может быть несколько моделей).

5.Изобразить ситуацию, описанную в задаче на чертеже (она может быть неоднозначной в геометрическом смысле).

6.Перевести задачу с естественного языка на математический.

7.Привести несколько математических моделей решения задачи, выбрать рациональное с точки зрения рассматриваемой реальной ситуации.

8.Установить требуемую точность (допустимую погрешность) результата.

9.Оценить, достаточно ли данных для построения математической

102

модели объекта, есть ли лишние данные.

10. Выбрать из предложенных математизаций одного объекта ту, которая соответствует заданному условию.

103

задачно-классификационный компонент: (признаки классификации задач на приложения -по области приложений математики; по математическим методам решения; по сложности математизации условия; по назначению в обучении; по способу представления; по полноте данных)

104

Рис. 5. Структура содержательно-методологической линии практических приложений математики в школе.

105

Подобные умения также могут быть сформированы при организации бесед на прикладную тематику как эвристического, так и репродуктивного характера (пример такой беседы имеется в статье «Беседы об угле зрения»105), выполнении проектов и проведении учебных исследований, связанных с процессом математизации реальности, но, в первую очередь, при решении специально подобранных задач, связанных с практическими приложениями математики. Перечисленные прикладные математические умения и типы заданий, способствующие формированию таких умений, дают возможность учителю проектировать содержание линии, ее этапов.

***

Итак, целесообразность выделения линии ППМ следует из современных целей школьного математического образования, отраженных в соответствующих нормативных документах, и назревшей потребности систематизировать такие приложения, определить цели и результаты их изучения. Методологическая функция линии ППМ состоит в изучении понятий и методов, объединяющих содержание не только методических, но и предметных линий всего школьного курса математики. К ее базовому понятию естественно отнести понятие математической модели, т.к. оно проявляется во всех средствах обучения приложениям математики в школе. Математическим методом линии является метод математического моделирования.

Принципы конструирования линии ППМ:

1.Математизации знаний.

2.Соответствия областей практических приложений математики познавательным возможностям и интересам учащихся.

3.Доступности для изучения на школьном уровне средств математизации знаний.

4.Достоверности содержания практических приложений математики.

105 Егупова М.В. Беседы об угле зрения. // Математика в школе, 2008. №9. - С. 69-73.

106

5. Открытости содержания линии.

Общие цели реализации линии ППМ:

1.Формирование системы математических знаний во взаимосвязи с их практическими приложениями к изучению окружающего мира.

2.Формирование прикладной математической грамотности, понимаемой как способность использовать математику для описания действительности и решения задач реального мира методом математического моделирования.

3.Демонстрация идей математизации наук через знакомство с теоретическими основами практических приложений математики.

Этапы реализации линии ППМ: пропедевтический, подготовительный, основной и заключительный.

Уровни сложности задач на приложения:

I. В задаче имеется прямое указание на математическую модель.

II. Прямого указания на модель нет, но объекты и отношения задачи легко соотносимы с соответствующими математическими объектами и отношениями.

III. Объекты и отношения задачи соотносимы с математическими объектами и отношениями, но неоднозначно. Требуется учет реально сложившихся условий.

IV. Объекты и отношения задачи явно не выделены или их математические эквиваленты неизвестны школьникам.

Определение уровня сложности задачи на приложения в практической работе учителя целесообразно проводить по двум критериям: новизна для школьников объектов и отношений содержательной модели задачи; сложность подбора математических эквивалентов к этим объектам и отношениям.

Прикладные математические умения школьников:

0 этап. Математизация (анализ условия).

0.1. Выделять объекты окружающей действительности, которые

107

могут быть описаны средствами школьного курса математики.

0.2.Заменять исходные объекты и отношения их математическими эквивалентами. Описывать эти объекты и отношения на языке математики.

1 этап. Формализация (построение математической модели условия).

1.1.Устанавливать соответствие между содержательной и математической моделью объекта в зависимости от предъявленных условий.

1.2.Соотносить реальные объекты различной природы с одной математической (геометрической) моделью.

1.3.Описывать реальный объект несколькими математическими (геометрическими) моделями.

1.4.Оценивать полноту исходных данных для построения математической модели.

2 этап. Внутримодельное решение.

2.1.Выбирать рациональные методы исследования реальных объектов в зависимости от поставленной задачи.

2.2.Составлять математическую модель с учетом требуемой точности описания реальных объектов задачи.

3 этап. Интерпретация результата.

3.1.Анализировать использованные математические методы решения

сточки зрения их рациональности для исследования реального объекта.

3.2.Интерпретировать результат исследования математической модели с требуемой погрешностью.

Структурные компоненты линии ППМ: содержательный, включающий содержание учебного материала, базовое понятие, этапы метода математического моделирования; деятельностный, представленный прикладными математическими умениями школьников; задачно-классификационный, содержащий систему классификаций задач на приложения (она будет дана полностью в следующем разделе, здесь

108

представлена классификация по уровням сложности); процессуальный, в котором выделены временные этапы реализации линии.

109