Бусыгин

241

α+= inf A+, α– = sup A–.

Для этих чисел справедливо соотношение α– < α+; в противном случае нашелся бы общий элемент α A–, α A+, что противоречит нерефлексивности }.

Покажем, что f(α+) { p { f(α–), т.е. α+ A+ и α– A–. Предположим противное. Пусть, например, w { p { f(α+). В таком случае в силу (A3) существует γ>0, такое что для лотереи w♦γ♦f(α+) справедливо соотношение

w♦γ♦f(α+) } p.

Поскольку

w♦γ♦f(α+) = w ♦γ♦ (b ♦α+♦ w) = b ♦ α+(1–γ) ♦ w = f(α+(1–γ)),

то это означает, что f(α+(1–γ)) } p. Значит, α+(1–γ) A+, а это противоречит определению

числа α+. Итак, предположение f(α+) } p неверно. Поэтому f(α+) { p. Рассуждения для α– аналогичны. Таким образом,

f(α+) { p { f(α–).

Если сопоставить это с вытекающим из Теоремы 5 и α– < α+ соотношением f(α– ) { f(α+),

то

f(α–) ~ p ~ f(α+).

Таким образом, мы можем выбрать U(p) = α+. Существование числа U(p) доказано. Единственность числа U(p) следует из Теоремы 5.

Теперь покажем, что U(p) есть функция полезности. Из Теоремы 5 следует, что из двух лотерей из f([0,1]) хуже та, коэффициент которой меньше и обратно:

f(α) { f(β) α < β.

Для двух произвольных лотерей p, q S соотношение p { q эквивалентно тому, что f(U(p)) { f(U(q)). Поэтому

p { q U(p) < U(q).

*

Докажем теперь, что построенная таким образом функция является единственной линейной функцией, представляющей рассматриваемые предпочтения.

Теорема 7.

Функция полезности U( ), такая что f (U(p)) ~ p, является линейной.

Эта функция — единственная (с точностью до линейного преобразования) линейная функция полезности, представляющая данные предпочтения.

Доказательство: (Линейность)

Мы хотим доказать, что если p, q S, α [0,1], то выполнено

U(p♦α♦q) = αU(p) + (1–α)U(q).

241

242

При α=0 и α=1 доказываемое очевидно. Рассмотрим случай 0 < α < 1.

Пусть утверждение теоремы неверно, например, для некоторых p, q S

U(p♦α♦q) < αU(p) + (1–α)U(q).

Тогда можно подобрать числа 0 < β < U(p) и 0 < γ < U(q), такие что

U(p♦α♦q) = αβ + (1–α)γ,

откуда

p♦α♦q ~ f (αβ + (1–α)γ).

По свойствам операции комбинирования лотерей f (αβ + (1–α)γ) = b♦(αβ + (1–α)γ)♦w =

= (b♦β♦w)♦α♦(b♦γ♦w) = f(β)♦α♦f(γ).

Поскольку β < U(p), то f (β) { f (U(p)) ~ p, и по аксиоме (A2) получим f(β)♦α♦f(γ) { p♦α♦f(γ).

Аналогичным образом, поскольку γ < U(q), то верно соотношение f (γ) { f (U(q)) ~ q, и по аксиоме (A2)

p♦α♦f(γ) { p♦α♦q.

Получаем, в противоречие с нерефлексивностью отношения предпочтения {, цепочку соотношений

p♦α♦q ~ f(β)♦α♦f(γ) { p♦α♦f(γ) { p♦α♦q.

Аналогичным образом можно прийти к противоречию, предположив, что U(p♦α♦q) >

αU(p) + (1–α)U(q). Значит,

U(p♦α♦q) = αU(p) + (1–α)U(q). (Единственность)

Предположим, что V(.) — другая линейная функция полезности. Обозначим

V*(p) = V(p) – V(w). V(b) – V(w)

Данное преобразование является линейным. Покажем, что V*(p) = U(p). Поскольку V(.) линейна, то V*(p) также линейна. Кроме того, функции V*(.) и U(.) совпадают для худшей и лучшей лотерей:

V*(w) = U(w) = 0 и V*(b) = U(b) = 1.

Это означает, что функции V*(.) и U(.) в силу линейности совпадают на f([0,1]). Поскольку любая лотерея из S эквивалентна лотерее из f([0,1]), то V*(.) и U(.) совпадают на любой лотерее из S.

*

Сопоставляя доказанные в этом параграфе теоремы, видим, что мы, фактически, доказали Теорему 49. Правда, при этом мы использовали дополнительное предположение (A4). (Способ доказательства Теоремы 49 обрисован в задаче 5).

Теорема 8.

242

243

Если предпочтения на множестве простых лотерей S удовлетворяют предположениям (A1)-(A4), то существует представляющая их функция полезности U( ), имеющая вид Неймана—Моргенштерна. Такое представление единственно с точностью до линейного преобразования.

Задачи

1.Пусть отношение предпочтения на множестве лотерей, }, транзитивно и выполнено свойство (A2). Покажите, что если p } q, r } s, то p♦α♦r } q♦α♦s (α [0,1]).

2.Пусть отношение предпочтения на множестве лотерей, }, нерефлексивно и выполнено свойство (A2). Покажите, что если p ~ q, то p♦α♦q ~ q (α [0,1]).

3.Пусть выполнены свойства (A1)-(A3). Покажите, что если p } r } q, то найдется единственное α [0,1], такое что p♦α♦q ~ r.

4.Пусть выполнены свойства (A1)-(A3). Покажите, что если p ~ q, и r — произвольная лотерея, то p♦α♦r ~ q♦α♦r (α [0,1]).

5.Докажите Теорему 49, т.е. «подправьте» доказательства этого параграфа таким образом, чтобы не требовалось использовать предположение (A4).

Указание: Пусть p и q — две лотереи, такие что p } q. Тогда, как было показано выше, существует функция полезности Неймана—Моргенштерна, определенная на «отрезке» {r | p } r } q}. Пусть теперь s — любая лотерея. Тогда, по отрицательной транзитивности }, выполняется одно из трех соотношений:

p } s } q, s } p } q, p } q } s.

Предположим, что функция полезности Неймана—Моргенштерна, представляющая отношение предпочтения, определена на отрезке {r | p } r } q} и пусть s удовлетворяет соотношению: s } p } q (p } q } s) . Тогда существует (и единственно) число α (β) такое, что

p = s ♦α♦q (q = p♦β♦ s)

Определим U( ) в последних двух случаях на основе соотношений:

U(p) = α U(s ) + (1– α)U(q) (U(q ) = β U(p ) + (1– β)U(s)).

Демонстрация линейности определенной таким образом функции в значительной степени воспроизводит этапы доказательства теоремы в частном случае, когда U( ) определена лишь на «отрезке» {r | p } r } q}.

Предпочтения потребителя в условиях неопределенности

Модифицируем модель поведения потребителя, чтобы учесть в ней неопределенность. Следуя Эрроу, мы будем различать блага не только по их физическим характеристикам, но и по состояниям мира, в которых они потребляются. Будем называть такие блага контингентными или условно-случайными. Каждое контингентное благо характеризуется двумя

243

244

индексами — индексом блага k K, и индексом состояния мира s S. Тогда xks — количество блага k, которое потребитель потребил (планирует потребить) в состоянии мира s.

Таким образом, к параметрам экономики добавляется множество состояний мира S = {1,

..., s^}. Мы будем считать его конечным. Потребляемый набор благ для i-го потребителя

будет описываться вектором xi ={xiks}(k,s). В предположении о том, что потребитель состояниям мира приписывает вероятности их реализации µis, каждому такому потребитель-

скому набору xi соответствует случайная величина (и лотерея), которую мы будем обозначать x~i (это l-мерная дискретная случайная величина, принимающая значения xis с вероятностями µis). Следуя сложившейся традиции, будем предполагать, что на множестве этих случайных величин потребитель имеет неоклассические (рациональные) предпочтения, которые допускают представление функцией полезности. Эту функцию полезности будем обозначать Ui( ). В этой целевой функции учтены как полезности для него каждого товара в каждом состоянии мира (например, зонт полезнее в дождь), так и его личные гипотезы о вероятностях событий.

Поскольку в этом параграфе анализируется поведение одного и того же потребителя, индекс i будем опускать.

В предположении, что оценки вероятности состояний мира у данного потребителя не меняются, мы можем считать, что его функция полезности U( ) задана на различных потребительских наборах, и писать U(x) вместо U(x~).

Различают следующие типы потребителей в соответствие с их поведением в ситуациях с неопределенностью (свойствами предпочтений):

Определение 2.

Будем называть потребителя имеющим неприятие риска, если его функция полезности U( ) (как функция x) квазивогнута.

Будем называть потребителя имеющим строгое неприятие риска или рискофобом, если его функция полезности U( ) строго квазивогнута

Будем называть потребителя нейтральным к риску, если U( ) линейна.

Будем называть потребителя рискофилом, если U( ) строго квазивогнута.

Напомним, что функция квазивогнута тогда и только тогда, когда множества потребительских наборов, предпочитаемых наборам, на кривой безразличия, выпуклы для каждой кривой безразличия. Вогнутость функции влечет за собой ее квазивогнутость, но не наоборот.

Рис. 50 иллюстрирует эти понятия для случая одного (физического) товара и двух состояний мира. На графиках изображены кривые безразличия для потребителей с разным отношением к риску в предположении, что x1 —потребление данного блага в первом, а x2 — во втором состоянии мира.

244

245

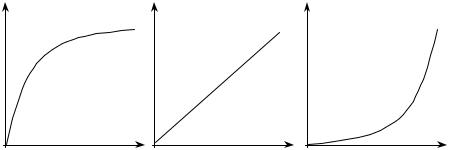
Рисунок 50. Кривые безразличия для потребителей с разным отношением к риску: а) рискофоб, б) нейтральный к риску, в) рискофил

В дальнейшем мы всюду будем предполагать, что функция U( ) имеет вид Неймана— Моргенштерна (аддитивная по вероятностям функция). Это частный, но наиболее удобный и поэтому наиболее часто используемый для анализа случай функции полезности U( ):

U(x) = Ûµsu(xs),

s S

где µs — оценки потребителем вероятностей состояний мира s S, xs X — потребительский набор в состоянии мира s (контингентный потребительский набор), а u(xs) —

(функция Бернулли) рассматриваемого потребителя

u( ): X &Ê,

не зависящая от состояния мира, а зависящая только от потребления благ как таковых.

частный, но наиболее удобный и поэтому наиболее часто используемый для анализа случай функции полезности U( )

Мы будем предполагать, что эта функция является возрастающей. Вероятности, заложенные в функции полезности участника могут быть и ошибочными, поэтому в общем случае их следует рассматривать как субъективные вероятности.

Напомним, что полезность по Нейману-Моргенштерну есть (субъективное) математическое ожидание полезности или просто ожидаемая полезность:

U(x) = Eu(x~).

Будем предполагать, что во всех рассматриваемых ниже ситуациях все необходимые условия существования функции полезности Неймана—Моргенштерна выполнены.

Переопределим для функции Неймана—Моргенштерна отношение к риску в терминах элементарной функции полезности.

Определение

Будем называть потребителя с глобальной функцией полезности U( ) типа Неймана— Моргенштерна имеющим (строгое) неприятие риска (рискофобом), если его элементарная функция полезности u( ) (строго) вогнута, нейтральным к риску, если она линейна, и (строго) предпочитающим риск (рискофилом) — если она (строго) выпукла.

245

Рисунок 51. Элементарные функции полезности для потребителей с разным отношением к риску: а) рискофоб, б) нейтральный к риску, в) рискофил

Можно показать, что из определения неприятия риска в терминах u( ) следует определение неприятия в терминах U( ), (обратное, вообще говоря, неверно). Из вогнутости u( ) следует вогнутость U( ), а следовательно и квазивогнутость.

В дальнейшем мы будем рассматривать только поведение экономических субъектов, характеризующихся неприятием риска, как более типичное.

Часто рассматривают ситуации, когда контингентные потребительские наборы содержат единственное благо — деньги. Соответствующие лотереи называют денежными. Количество денег, которое получает индивидуум в состоянии мира s (xs) будем называть доходом в этом состоянии мира (контингентным доходом). При этом используют следующие понятия (индекс блага опускаем).

Ожидаемый доход Ex~ — это математическое ожидание дохода. В данном случае он вычисляется как

Ex~= Ûµsxs.

s S

В терминах ожидаемого дохода рассмотренные выше три группы потребителей в зависимости от их отношения к риску характеризуются следующими соотношениями между ожидаемой полезностью денежной лотереи и полезностью ожидаемого дохода от нее:

–рискофилы: E(u(x~)) > u(E(x~)),

–рискофобы: E(u(x~)) < u(E(x~)),

–нейтральные по отношению к риску: E(u(x~)) = u(E(x~)).

Здесь x~ — любая «нетривиальная» случайная величина (формально это означает, что вероятность того, что она не совпадает со своим математическим ожиданием, не равна нулю).

Заметим, что соотношение E(u(x~)) > u(E(x~)) для всех случайных величин (так называемое неравенство Йенсена) выполнено тогда и только тогда, когда функция вогнута. Фактически это и есть определение вогнутой функции. Строгое неравенство E(u(x~)) < u(E(x~)) для произвольной «нетривиальной» случайной величины x~ выполнено тогда и только тогда, когда функция строго вогнута.

Безрисковым или гарантированным называется такой случайный потребительский набор x~, что в любом состоянии мира потребитель имеет один и тот же доход: xs = Ex~ s S.

246

247

Безрисковым или гарантированным эквивалентом75 данного потребительского набора x~ на-

зывается такой доход x*, что соответствующий безрисковый потребительский набор x~* дает потребителю ту же самую полезность:

Eu(x~) = Ûµsu(xs) = Eu(x~*) = u(x*).

s S

Величина ∆x называется вознаграждением за риск для данного потребительского набора x~, если Ex~– ∆x является безрисковым эквивалентом x~:

Eu(x~) = u(Ex~– ∆x).

Эта величина показывает, какую сумму денег (в терминах ожидаемого дохода) готов потерять потребитель за то, чтобы избавиться от риска.

У рискофобов безрисковый эквивалент ниже ожидаемого дохода от любой рискованной денежной лотереи (величина вознаграждения за риск положительна). Соответственно, у рискофилов он выше ожидаемого дохода (величина вознаграждения за риск отрицательна), а у нейтральных по отношению к риску потребителей совпадает (величина вознаграждения за риск равна нулю). Читателю предоставляется показать это самостоятельно.

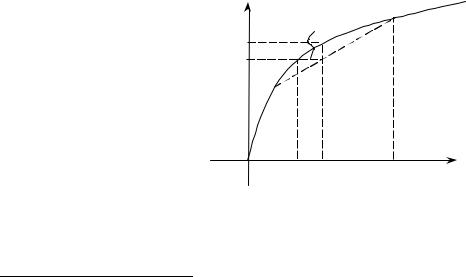
Проиллюстрируем введенные понятия графически. На Рис. 52 изображена элементарная функция полезности потребителя с неприятием риска (функция вогнута). Потребитель предполагает, что могут произойти два события (A и B) с некоторыми вероятностями (µA и µB). Его потребительский набор имеет вид x= (xA, xB), где xA и xB — доход, который получит потребитель, если произойдут события A и B соответственно. Как несложно понять, точка (Ex~, U) лежит на отрезке, соединяющей точки (xA, u(xA)) и (xB, u(xB)) и делит его в отношении µB к µA. Здесь Ex~ — ожидаемый доход набора, а U — полезность. Поскольку потребитель не любит риск, то график функции полезности лежит выше указанного отрезка, и ожидаемая полезность U = Eu(x~) больше полезности ожидаемого дохода u(Ex~). Гарантированный эквивалент x~ выбирается так, чтобы U(x~) = u(x*). Плата за риск ∆x равна разности между ожидаемой доходностью и доходностью гарантированного эквивалента.

x

Рисунок 52. Различные характеристики лотереи с двумя событиями

Пример 1. (Санкт-Петербургский парадокс)76

75Англ. certainty equivalent.

76Описание и объяснение этого парадокса приводятся в статье известного швейцарского ученого Даниила Бернулли: Daniel Bernoulli, "Specimen theoriae novae de mensura sortis", Commentarii academiae scientiarium imperialis Petropolitanae, T. V. Petropoli, 1738, 175-192 (рус. пер.: Д. Бернулли, "Опыт новой теории измере-

ния жребия", в кн. Теория потребительского поведения и спроса, — СПб.: Экономическая школа, 1993).

247

248

«Петр бросает вверх монету, пока она не упадет лицевой стороной вверх; если это происходит после первого броска, он должен дать Павлу 1 дукат, но если только после второго — 2 дуката, после третьего — 4, после четвертого — 8 и так далее, так что после каждого броска число дукатов удваивается. Спрашивается: какова оценка жребия для Пав-

ла?».

Ожидаемый доход от этой игры для Павла бесконечно велик, однако вряд ли кто согласиться заплатить за право участия в такой игре очень большую сумму. В этом и состоит парадокс. Объяснение парадокса состоит в том, что «ценность денег» для игрока не является постоянной. Она определяется некоторой возрастающей вогнутой элементарной функцией полезности.

Предположим, что исходный (безрисковый) доход игрока составляет сумму ω дукатов. В таком случае он сталкивается с лотереей, приносящей ему доход ω+2k–1 с вероятностью 2– k (k = 1, 2 , ..., ∞). Ожидаемый доход (с учетом цены p, уплаченной за участие в игре) равен

∞

Ex~= Û2–k(ω+2k–1 – p) = ∞.

k=1

Если элементарная функция полезности игрока — u( ), то ожидаемая полезность равна

∞

U = Eu(x~) = Û2–ku(ω+2k–1 – p).

k=1

Если x* — безрисковый эквивалент этой лотереи, то игрок будет готов заплатить за право участвовать в игре x* – ω.

Например, если u(x) = ln(x) и ω= 100, то максимальная цена, которую Павел будет готов отдать за участие в игре, определяется уравнением

∞

Û2–k ln(100 +2k–1 – p) = ln(100).

k=1

Отсюда, решая численно это уравнение, получим

p ≈4,36 < ∞,

то есть несколько больше 4 дукатов.

Задачи

6. Потребитель имеет элементарную функцию полезности u(x) = x. Он получает доход 9 с вероятностью 2/3 и доход 25 с вероятностью 2/3. Найти плату за риск.

7. Индивидуум имеет функцию полезности типа Неймана—Моргенштерна. Элементарная функция полезности строго возрастает и зависит только от одного аргумента (денег). Лотерея $3 и $5 с вероятностями 1/2 и 1/2 и лотерея $3 и $9 с вероятностями 2/3 и 1/3 для него эквивалентны. Может ли быть верным, что этот индивидуум

(а) рискофоб; (б) нейтрален к риску; (в) рискофоб?

8. Пусть есть одно благо (деньги), элементарная функция полезности потребителя имеет вид u(x) = x, а начальный запас (гарантированная сумма) денег равен $9. Существует

248

249

лотерейный билет, который может выиграть $0 с вероятностью 0,5 (если выпадет «орел») и $7 с вероятностью 0,5 («решка»). Рассмотрите три альтернативные ситуации:

(1)За какую сумму x потребитель купил бы такой билет?

(2)За какую сумму y потребитель согласился бы сам эмитировать (продать) такой лотерейный билет (можно считать, что его гарантированный запас состоит из 9-ти билетов по $1 выигрывающих в состоянии мира «орел» и 9-ти по $1 на «решку»)?

(3)Если потребителю подарят такой билет, за какую сумму z он бы его продал?

9.Рискофоб с элементарной функцией полезности (функцией Бернулли) вида u(x) = –1/x имеет $900 и лотерейный билет, который дает $900 с вероятностью 1/2 и $0 с вероятностью 1/2. За сколько он продал бы этот билет?

10.Богатство потребителя равно 100 д.е. Элементарная функция полезности равна квадратному корню из дохода. Лотерейный билет дает выигрыш 0 д.е. с вероятностью π и 20 д.е. с вероятностью (1 – π). Цена билета равна 5 д.е. При каких вероятностях потребитель

(1)купит билет?

(2)продаст билет (сам его эмитирует)?

(3)продаст билет, если ему его подарят?

(Решать не обязательно, достаточно составить неравенство)

11. Рассмотрим следующую игру: если игрок называет число a, то получает дополнительно к имеющейся у него сумме ω сумму a с вероятностью 1/3 и (–a) с вероятностью 2/3. Какое число назовет игрок, предпочтения которого описываются функцией полезности Неймана—Моргенштерна с элементарной функцией полезности u( )?

12. Пусть рискофоб, предпочтения которого описываются функцией полезности Нейма- на—Моргенштерна с элементарной функцией полезности u(x) = x, владеет суммой денег ω рублей и лотерейным билетом, выигрывающим a рублей с вероятностью 1/2. Покажите, что при уменьшении a до нуля цена, за которую он готов продать этот лотерейный билет, стремиться к величине ожидаемого (для данного рискофоба) выигрыша по этому билету.

13. Индивидуум, чьи предпочтения на лотереях описываются функцией полезности Ней- мана—Моргенштерна с элементарной функцией полезности u(x) = x, располагает суммой денег ω рублей. Ему предлагают приобрести лотерейный билет, выигрывающий a рублей с вероятностью 1/2. Пусть p — максимальная цена, которую он готов уплатить за лотерейный билет.

(1)Чему равна p при ω= 9 и a = 16?

(2)Покажите, что p ...

-растет при увеличении величины выигрыша a.

-растет при увеличении суммы денег ω.

-не может превышать величину a/4 рублей.

249

250

14. Нейтральный к риску фермер может посеять капусту на берегу реки и получить доход $1000 , но рискует потерять весь урожай при наводнении. Он может посеять вдали от берега, где урожайность на 20% меньше, но нет риска. Фермер оценивает вероятность наводнения в 0,1. Как он поступит без дополнительной информации? Сколько бы он отдал за точную информацию о наводнении?

15. Золотоискатель с запасом 900$, полезностью типа Неймана—Моргенштерна и функцией Бернулли вида u(x) = x решает, купить ли по цене 300$ золотоносный участок, где с равной вероятностью ожидает выигрыш в 900$ или ничего.

(A) За сколько он купил бы у геолога соответствующий прогноз, если положительный прогноз означает, что с вероятностью 0,75 золото есть, а отрицательный — что с вероятность 0,75 золота нет?

(B) Предположим, золотоискатель не купил прогноз, а застраховался на сумму в 300$ на случай отсутствия золота и купил участок. По какой цене продавались страховые контракты?

Задача потребителя при риске

В экономике с неопределенностью естественно ожидать заключения контрактов, условных по состояниям мира. Соответственно, блага следует рассматривать как условные по состояниям мира — контингентные (условно-случайные) блага. Каждое контингентное благо характеризуется парой (k, s). Контингентное благо естественно интерпретировать как актив, дающий право получить единицу блага k если (и только если) реализуется состояние мира s. Такой актив получил название актива Эрроу. (Нам понадобится понятие актива Эрроу ниже, когда речь пойдет о модели Раднера. В данном контексте это только интерпретация контингентного блага.)

Если ничто не препятствует заключению контрактов условных по состояниям мира (т.е. купле-продаже контингентных благ), то можно предположить, что любое контингентное благо можно обменять на любое другое контингентное благо. Иными словами, можно предположить, что любое благо k1 в любом состоянии мира s1 можно поменять (прямо или косвенно) на любое благо k2 в любом состоянии мира s2. Это предположение о полноте рынков контингентных благ.

Следует отметить, что предположение о полноте рынков контингентных благ является достаточно ограничительным и, как правило, не позволяет адекватно моделировать реальные рынки с риском. Тем не менее, модели, основанные на этом предположении, оказывается полезными при анализе реальных феноменов и понимании причин фиаско рынка при наличии неопределенности.

Другое предположение, которое мы сделаем — это предположение о свободной конкуренции на рынках контингентных благ. С точки зрения задачи потребителя — это стандартное предположение о том, что потребитель считает цены данными. Через pks мы будем обозначать рыночную цену контингентного блага (k, s) (это цена контракта на поставку единицы блага k в ситуации, если реализуется состояние мира s, т.е. цена соответствующего актива Эрроу).

Эти предположения позволяют записать задачу потребителя:

Ui(xi) = Ûµsui(xis) → max xi

s S

ÛÛpksxiks <ÛÛpksωiks, s Sk K s Sk K

xis Xi s S.

250