Бусыгин

211

ваемым благом в каждом технологическом процессе является (l + 1)-ое благо — деньги.65 В анализе удобно описывать технологии с помощью функции издержек cj(y1,..., yl) (которая каждому вектору объемов первых l благ сопоставляет необходимые для производства этих объемов затраты (l + 1)-го блага). Для того чтобы формально установить связь функции издержек с технологическим множеством предприятия j (Yj), рассмотрим следующую задачу:

r →min r

(y1,..., yl, –r) Yj.

Функция cj(y) сопоставляет каждому вектору выпусков y= (y1,..., yl) значение целевой функции этой задачи. В предположении замкнутости технологического множества оптимальное решение существует, если существует хотя бы одно допустимое решение. В дальнейшем мы будем предполагать, что множество значений выпусков y, при которых существует допустимое решение рассматриваемой задачи, совпадает с Êl+. Это означает, что функция издержек cj( ) определена на множестве Êl+, т.е. все неотрицательные выпуски возможны. Заметим, что выпуклость множества Yj гарантирует выпуклость функции cj( ).

Заметим, что функция издержек однозначно описывает технологическое множество в том случае, если выполнения для y и r неравенств

r >cj(y), y>0,

эквивалентно принадлежности множеству допустимых технологий Yj соответствующего вектора (y, –r). Для этого можно дополнительно потребовать, чтобы технологическое множество Yj удовлетворяло свойству свободы расходования (можно «выбрасывать» блага), то есть, чтобы из допустимости технологии (y, –r) всегда следовала допустимость технологии (y′, –r′), такой что (y′, –r′) <(y, –r).

Мы будем рассматривать два типа экономик. В одной из них (экономика EQ) предполагается, что потребитель не сталкивается с ограничением типа zi >0 (может «брать в долг» неограниченную сумму денег). В другой это ограничение принимается (экономика E+Q).

Под допустимым состоянием квазилинейной экономики EQ мы будем понимать такое состояние {(x1, z1), ..., (xm, zm), (y1, r1), ..., (yn, rn)}, что выполнены неравенства:

Ûxik <Ûyjk k = 1, ..., l,

i I j J

Ûzi + Ûrj = Ûωi,

i I j J i I

rj >cj(yj) j J,

xi >0 i I, yj >0 j J.

Соответственно, под допустимым состоянием квазилинейной экономики E+Q мы будем понимать такое состояние {(x1, z1), ..., (xm, zm), (y1, r1), ..., (yn, rn)}, что выполнены все вышеприведенные условия, и, кроме того, zi >0 i I.

65 Вообще говоря, мы можем предполагать, что некоторые из первых l благ затрачиваются в производстве, и для них может выполняться yj < 0; это никак не изменит выводов.

211

212

Характеристика Парето-оптимальных состояний в квазилинейных экономиках

Квазилинейностью предпочтений потребителей объясняется ряд особых свойств рассматриваемой экономики. В частности, анализировать Парето-оптимальные состояния в квазилинейной экономике можно с помощью следующей задачи оптимизации:

Ûvi(xi) – Ûcj(yj) →max x, y

i I j J

Ûxik <Ûyjk k = 1, ..., l, (W)

i I j J

xi >0 i I, yj >0 j J.

Другими словами, верна следующая теорема, дающая полное описание границы Парето экономики EQ.

Теорема 1.

Состояние {(x^1, z^1), ..., (x^m, z^m), (y^1, r^1), ..., (y^n, r^n)} является Парето-оптимальным состоянием в квазилинейной экономике EQ тогда и только тогда, когда

(x^1, ..., x^m, y^1, ..., y^n)

является решением задачи (W),

r^j = cj(y^j)

и

Ûz^i =Ûωi – cj(y^j).

i I i I

Доказательство:

1) Докажем сначала, что если {(x^1, z^1), ..., (x^m, z^m), (y^1, r^1), ..., (y^n, r^n)} — Парето-

оптимальное состояние в квазилинейной экономике EQ, то набор (x^1, ..., x^m, y^1, ..., y^n) является решением задачи (W).

Напомним, что Парето-оптимальное состояние при любом i0 I является решением следующей задачи условной максимизации:

vi0(xi0) + zi0 →max vi(xi) + zi >vi(x^i) + z^i i ≠i0

Ûxik <Ûyjk k = 1, ..., l,

i I j J

Ûzi + Ûrj <Ûωi,

i I j J i I

rj >cj(yj) j J,

xi >0 i I, yj >0 j J.

Как несложно показать, в этой задачи первое, третье и четвертое неравенства можно заменить на равенства, не изменяя множество решений задачи. Выражая из этих равенств zi и

212

213

rj и исключая их из оставшихся неравенств, видим, что данная задача сводится к задаче

(W).

2) Обратно, пусть (x^1, ..., x^m, y^1, ..., y^n) является решением задачи (W). Рассмотрим произвольные z^j, удовлетворяющие балансам

является допустимым состоянием экономики EQ. Докажем, что оно Парето-оптимально. Пусть это не так, и существует другое допустимое состояние экономики EQ,

S~ = {(x~1, z~1), ..., (x~m, z~m), (y~1, r~1), ..., (y~n, r~n)},

такое что для всех потребителей (i I)

vi(x~i) + z~i >vi(x^i) + z^i ,

и существует, по крайней мере, один потребитель i0, для которого выполнено

vi0(x~i0) + z~i0 > vi0(x^i0) + z^i0.

Складывая эти неравенства, получаем

Ûvi(x~i) – Ûcj(y~j) > Ûvi(x^i) – Ûcj(y^j).

i I j J i I j J

Поскольку (x~1, ..., x~m, y~1, ..., y~n) является допустимым в задаче (W), то это означает, что существование состояния S~ противоречит оптимальности (x^1, ..., x^m, y^1, ..., y^n) в задаче

(W).

*

Первая часть доказанной теоремы для экономики E+Q в общем случае не верна (см. нижеприведенный пример). Вторая часть верна при дополнительном предположении о том, что совокупные начальные запасы достаточно велики.

Как видно из вышеприведенной теоремы, задача поиска Парето-оптимума для экономики EQ эквивалентна задаче (W). В то же время множество допустимых состояний для эконо-

213

214

мики E+Q является подмножеством множества допустимых состояний для экономики EQ. Поэтому не исключена ситуация, в которой Парето-оптимум экономики E+Q не является Парето-оптимумом экономики EQ и, следовательно, не будет решением задачи (W).

Несложно придумать пример экономики E+Q и Парето-оптимума этой экономики, так чтобы в этом Парето-оптимуме ограничение zi > 0 оказалось существенным для одного из потребителей, и при снятии этого ограничения можно было бы увеличить полезность одного из потребителей, не уменьшая полезность остальных. Читатель может сконструировать такой пример самостоятельно.

Но даже если в Парето-оптимуме экономики E+Q все ограничения zi > 0 выполняются как строгие неравенства, снятие данных ограничений может позволить осуществить Паретоулучшение. Приведем пример.

Пример 1.

Рассмотрим экономику с одним потребителем (m = 1), одним производителем (n = 1) и двумя благами (l + 1 = 2). Для упрощения обозначений индексы будем опускать. Предпочтения потребителя заданы функцией v(x) = 5x3 – 9x2 + 6.9x, а технологическое множество фирмы — функцией издержек c(x) = x4. Обе функции являются возрастающими при x > 0, поэтому y = x, r = c(x) и z + r = ω, так что поиск Парето-оптимума сводится к максимизации функции

v(x) – c(x)

при ограничениях x >0 и c(x) <ω. Здесь ограничение c(x) <ω соответствует ограничению z >0. Можно переписать последнее ограничение в виде x <c–1(ω).

–0,025

–0,05

–0,075

–0,1

0,125

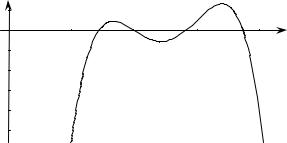
Рисунок 44. Пример существенности ограничения неотрицательности линейного члена

Пусть ω= 1, при этом c–1(ω) = 1. Как видно на Рис. 44 функция v(x) – c(x) имеет два локальных максимума: x1 ≈0.83473 и x2 ≈1.6988. Только второй из этих максимумов является глобальным. Парето-оптимум экономики E+Q достигается при x = x1, поскольку максимизация идет на отрезке [0, 1]. В то же время Парето-оптимум экономики EQ и, следовательно, решение задачи (W) достигается при x = x2.

В этом примере ключевым моментом является то, что функция v( ) не является вогнутой. Можно было построить подобный пример иначе: так, чтобы функция v( ) была вогнутой, но функция издержек не была выпуклой. Таким образом, для доказательства аналога первой части предыдущей теоремы в «выпуклой» экономике E+Q следует потребовать, чтобы все функции vi( ) были вогнутыми, а функции cj(yj) — выпуклыми. Аналогом этой теоремы для случая экономики E+Q является следующая теорема.

214

215

Теорема 2.

1) Предположим, что функции vi( ) вогнуты, а функции издержек cj( ) выпуклы, и пусть

S^ = {(x^1, z^1), ..., (x^m, z^m), (y^1, r^1), ..., (y^n, r^n)} —

Парето-оптимальное состояние в квазилинейной экономике E+Q, причем z^i > 0 i. Тогда набор (x^1, ..., x^m, y^1, ..., y^n) является решением задачи (W).

2) Обратно, пусть (x^1, ..., x^m, y^1, ..., y^n) является решением задачи (W), причем

Ûωi – Ûcj(y^j) >0.

i I j J

Тогда для произвольных z^1, ..., z^m >0, удовлетворяющих балансам

Ûz^i = Ûωi – cj(y^j)

i I i I

набор {(x^1, z^1), ..., (x^m, z^m), (y^1, c1(y^1)), ..., (y^n, cn(y^n))} является Парето-оптимальным со-

стоянием квазилинейной экономике E+Q.

Доказательство:

1) Доказательство опирается на следующее вспомогательное утверждение: если S^ — Па- рето-оптимум в экономике E+Q, удовлетворяющий условиям теоремы, то он также является Парето-оптимумом в соответствующей экономике EQ. Если это утверждение верно, то доказываемое является тривиальным следствием предыдущей теоремы.

Докажем это вспомогательное утверждение от противного. Пусть в соответствующей экономике EQ существует допустимое состояние

S~ = {(x~1, z~1), ..., (x~m, z~m), (y~1, r~1), ..., (y~n, r~n)},

которое доминирует по Парето состояние S^. Рассмотрим выпуклую комбинацию этих двух состояний:

S(α) = αS^ + (1 – α)S~, α [0, 1].

Существует достаточно малое α> 0, такое что S(α) является допустимым в экономике E+Q. Однако при α> 0 состояние S(α) представляет собой Парето-улучшение в экономике E+Q по сравнению с S^, что противоречит предположению теоремы.

Подробное изложение доказательства оставляется в качестве упражнения. 2) Доказательство оставляется в качестве упражнения.

*

Приведенные выше результаты позволяют нам в случае квазилинейной экономики использовать задачу (W) для анализа Парето-оптимальных состояний.

В ситуации, когда функции vi( ) строго вогнуты, а функции cj( ) выпуклы, решение задачи (W) единственно, поэтому два Парето-оптимальных состояния в экономике EQ (в экономике E+Q, если z~i и z`i положительны)

(x~1, z~1), ..., (x~m, z~m), (y~1, r~1), ..., (y~n, r~n)}, (x`1, z`1), ..., (x`m, z`m), (y`1, r`1), ..., (y`n, r`n)}, —

215

216

могут различаться лишь объемами потребления (l+1)-го блага. Другими словами, x~i = x`i

i I и y~j = y`j j J.

Поэтому, как несложно заметить, в случае экономики EQ граница Парето представляет собой гиперплоскость вида (читателю предлагается доказать этот результат самостоятельно)

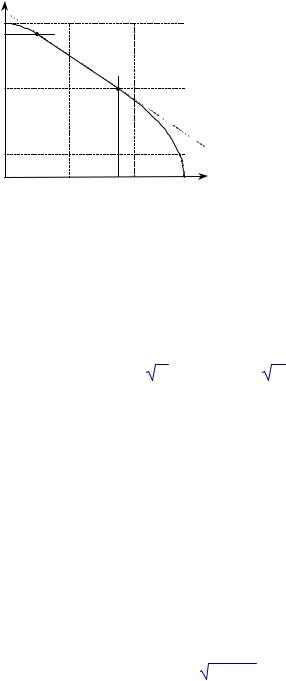
Рисунок 45. Парето-граница в экономике типа E+Q

В экономике E+Q граница Парето может «загибаться» из-за того, что некоторые из ограничений zi >0 являются существенными, что иллюстрирует следующий пример.

Пример 2.

На Рис. 46. изображена Парето-граница в экономике типа E+Q со следующими параметрами: 2 блага (l + 1 = 2), 2 потребителя, с функциями полезности

u1 = 2 x1 + z1 и u2 = 4 x2 + z2,

и один производитель с функцией издержек

c(y) = y.

Начальные запасы 2-го блага равны 10.

Несложно проверить, что решение задачи (W) дает x1 = 1 и x2 = 4. Однако это решение описывает точки границы Парето только при u1 [2; 7]. Парето-граница при этом имеет вид

u2 = 15 – u1.

При u1 [0; 2] Парето-граница имеет вид u2 = 14 – u412.

При u1 [7; 11] Парето-граница имеет вид u2 = 4 11 – u1 .

216

217

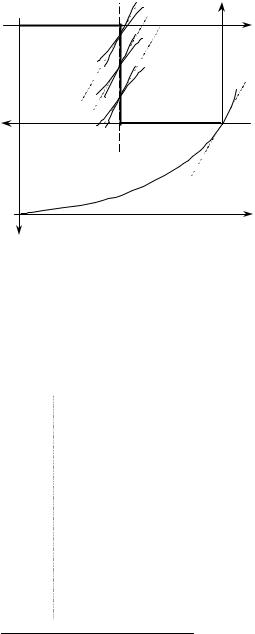
В случае двух благ можно привести графическую иллюстрацию Парето границы экономики типа E+Q на основе диаграммы Эджворта (см. Рис. 46). Жирная линия представляет собой границу Парето.

Так как в достаточно широком классе случаев решения задачи (W) описывают Паретограницу, то целевую функцию задачи (W) можно использовать для решения вопроса о принадлежности некоторого допустимого состояния к Парето-границе. В связи с этим, естественно рассматривать функцию

W(x, y) = Ûvi(xi) – Ûcj(yj)

i I j J

в качестве индикатора благосостояния. Основанием для этого является следующая теорема.

Рисунок 46. Парето-граница экономики типа E+Q на основе диаграммы Эджворта

Пусть

S~ = {(x~1, z~1), ..., (x~m, z~m), (y~1, r~1), ..., (y~n, r~n)}, S` = {(x`1, z`1), ..., (x`m, z`m), (y`1, r`1), ..., (y`n, r`n)} —

допустимые состояния экономики EQ (E+Q ). Тогда выполнено следующая теорема.

Теорема 3.

1) Если каждый из потребителей в состоянии S~ имеет не меньшую полезность, чем в состоянии S`, т.е.

vi(x~i) + z~i > vi(x`i) + z`i i,

и

Ûz`i + Ûcj(y`j) = Ûωi ,66

то

W(x~, y~) > W(x`, y`),

66 Это условие будет, например, выполнено в общем равновесии.

217

218

причем если существует потребитель i0, такой что

vi0(x~i0) + z~i0 > vi0(x`i0) + z`i0

(т.е. состояние S~ доминирует S` по Парето), то

W(x~, y~) > W(x`, y`).

2) Для экономики EQ выполнено и обратное: если для состояний S~ и S` верно W(x~, y~) > W(x`, y`), то можно подобрать z~1′, ..., z~m′ такие, что состояние экономики

{(x~1, z~1′), ..., (x~m, z~m′), (y~1, r~1), ..., (y~n, r~n)},

будет допустимым, причем

vi(x~i) + z~′i > vi(x`i) + z`i i.

Доказательство:

Доказательство оставляется в качестве упражнения.

*

Первая часть данного утверждения говорит о том, что любое Парето-улучшение сопровождается ростом индикатора W( ). Смысл второй части приведенного утверждения состоит в том, что если W(x~, y~) > W(x`, y`), то можно в состоянии S~ произвести такие трансферты

(перераспределить деньги), что новое состояние будет строго доминировать состояние S` по Парето. Заметим, что некоторые zi при этом могут оказаться отрицательными, поэтому вторая часть утверждения неприменима к экономике E+Q.

В Парето-оптимуме квазилинейной экономики индикатор благосостояния достигает максимума. Пусть W^ — это максимальное значение. Разность между W^ и уровнем индикатора W(S) в некотором состоянии S называется чистыми потерями благосостояния:

DL = W^ – W(S).

Сравнение уровней благосостояния в анализируемом состоянии и в идеальной ситуации позволяет количественно оценить, насколько далеко данное неэффективное состояние от границы Парето, и сколько экономика в целом теряет вследствие неэффективности.

Характеристика поведения потребителей в квазилинейных экономиках

В дальнейшем сравниваются потребительские наборы, которые оказываются рыночными равновесиями при различных организациях рынков (совершенная конкуренция, монополия, олигополия и т.д.). При этом всюду предполагается, что потребители рассматривают рыночные цены как данные. Другими словами, определяя предпочитаемый потребительский набор (xi, zi) при рыночных ценах благ (p, 1), потребитель в экономике EQ решает следующую задачу:

vi(xi1,..., xil) + zi → max

(Будем обозначать эту задачу через C+Q). Здесь через βi обозначен доход потребителя.

218

219

Имеют место следующие результаты, характеризующие оптимальный выбор потребителя.

Теорема 4.

Предположим, что (x-i, z-i) — решение задачи потребителя CQ при ценах p. Тогда x-i является решением следующей задачи

И обратно, пусть x-i — решение задачи (☺), тогда (x-i, βi – px-i) — решение задачи CQ при ценах p.

Доказательство:

Доказательство оставляется в качестве упражнения.

*

Это означает, что спрос потребителя на первые l благ не зависит от его дохода. Аналог этого результата верен и в случае задачи C+Q, когда допустимые потребительские наборы удовлетворяют дополнительному условию zi> 0, что показывает следующая теорема.

Теорема 5.

Предположим, что vi( ) — вогнутая функция, а (x-i, z-i), — решение задачи потребителя C+Q при ценах p (соответствующей экономике E+Q), такое что z-i > 0. Тогда x-i является решением следующей задачи

Доказательство:

Доказательство оставляется в качестве упражнения.

*

Предположим дополнительно, что vi( ) — непрерывно дифференцируемая функция. Тогда для решения задачи оптимального выбора потребителя CQ (или C+Q при zi > 0) должно выполняться следующее условие

vi(x-i) <p,

причем если x-ik > 0, то

∂ - vi(xi) ∂xik = pk .

Таким образом, если решение задачи потребителя внутреннее (x-i > 0) и, кроме того, zi > 0 в случае задачи C+Q), то

219

220

vi(x-i) = p.

Другими словами, градиент функции vi( ), вычисленный для набора благ, совпадающего с рыночным спросом потребителя, равен вектору рыночных цен этих благ. Таким образом, градиент функции vi( ) представляет собой обратную функцию спроса pi(xi) i-го потребителя — вектор цен первых l благ, при котором потребитель предъявляет спрос именно на этот набор благ.

В классе квазилинейных экономик важную роль играет случай когда предпочтения всех потребителей, помимо свойства квазилинейности обладают свойством сепарабельности, т.е. функции полезности таких потребителей представимы в виде

ui(xi1,..., xil, zi) = vi(xi1,..., xil) + zi = Ûvik(xik) + zi.

k

Если функция полезности i-го потребителя имеет такой вид, то задачу потребителя CQ можно разложить на l задач — по одной на каждое благо кроме (l+1)-го:

vik(xik) – pkxik → max xik>0 (CQk)

Теорема 6.

Если x-i — решение задачи потребителя CQ при ценах p, то x-ik — решение задачи CQk при

цене pk. Обратно, если x-ik — решение задачи CQk при цене pk при k = 1, ..., l, то x-i = (x-i1, ..., x-il) — решение задачи CQ при p= (p1, ..., pl).

Доказательство:

Доказательство оставляется в качестве упражнения.

*

Из данной теоремы следует, что функция спроса на k-е благо зависит только от цены на это благо, т.е. имеет вид xik(pk).

В этом случае (при условии дифференцируемости) необходимое условие оптимальности потребительского набора (x-i, -zi) (как в случае экономики EQ, так и в случае E+Q при zi > 0) имеет вид:

Это условие является также и достаточным, если vik( ) — вогнутые функции.

Из Теоремы Ошибка! Источник ссылки не найден. следует, что, вместо исходной задачи мы можем использовать для анализа спроса на k-е благо задачу CQk. Мы будем предполагать, что функция vik(xik) дважды дифференцируема, имеет положительную производную и строго вогнута. Строгая вогнутость гарантирует, в числе прочего, что если решение задачи CQk существует, то оно единственно. Очевидно, что это решение есть значение функции спроса рассматриваемого потребителя на k-е благо при данном pk, xik(pk).

Рассмотрим условия существования решения задачи CQk. (Заметим, что из Теоремы Ошибка! Источник ссылки не найден. следует, что решение исходной задачи CQ в слу-

220