Бусыгин

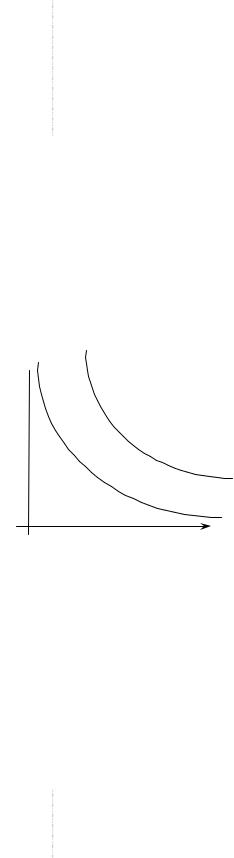
141

Множество требуемых затрат

Определение 4.

Для каждого вектора выпуска y множество требуемых затрат V(y) — это множество векторов затрат, обеспечивающих этот выпуск при данном технологическом множестве

Y, т.е.

V(y) = {r| (–r, y) Y}.

Из предполагаемых свойств Y вытекают некоторые свойства множества V(y) и соответствующего отображения V( ):

1.Из выпуклости Y следует выпуклость множеств V(y):

2.Из свободы расходования для Y следует свобода расходования для множеств V(y):

r V(y), r′ >r r′ V(y).

Заметим, что обратное, вообще говоря, неверно.

Обычно предполагается монотонность отображения V( ), т. е. вложенность множеств V(y):

y<y′ V(y′) V(y).

r2

V(y′)

V(y)

y<y′

r1

Рисунок 27. Монотонность V( )

Множества V(y), как и Y, в предположении свободного расходования можно строить по производственной функции:

V(y) = {r| f(r) > y}.

Обратно, в случае однопродуктовой технологии (y Ê) можно определить на основе V( ) производственную функцию следующим образом:

f(r) = max y.

y:r V(y)

Теорема 13.

Если отображение V( ) монотонно, то соответствующая производственная функция монотонна, а если к тому же множества V(y) выпуклы, то она квазивогнута.

Доказательство:

Доказательство этого утверждения оставляется читателю в качестве упражнения.

141

142

■

В терминах множеств V(y) можно определить изокванты для данной технологии

Q(y) = {r V(y) | r V(y′), y′> y}.

Это множество таких векторов затрат r, которые позволяют произвести y, но не позволяют произвести больше y. Таким образом, изокванта Q(y) — это граница множества V(y).

Например, для производственной функции Кобба-Дугласа с двумя видами затрат имеем

Y = {(–r1, –r2, y) | y <rα1 r12–α}, V(y) = {(r1, r2) | y <rα1 r12–α}, Q(y) = {(r1, r2) | y = rα1 r12–α}.

Напомним, что через w мы обозначили цены затрачиваемых ресурсов (часть общего вектора цен p, соответствующая –r).

Функция издержек

По аналогии с Задачей 3 рассмотрим следующую задачу

Задача 4.

wr→min r r V(y).

Обозначим множество цен факторов, на котором существует решение Задачи 4 при объеме выпуска y, через W(y).

Определение 5.

Функция издержек c(w, y) — это значение целевой функции Задачи 4; для каждого вектора выпуска y и вектора цен факторов w W(y) она указывает минимальную величину издержек, при которых в соответствии с данной технологией можно произвести y.

Если технологическое множество задано производственной функцией y <f(r), то Задача 4 примет вид:

wr→min r y <f(r).

Функция издержек обладает следующими свойствами.

Теорема 14. (Свойства функции издержек c(w, y) выпуклой технологии) Функция издержек c(w, y)

142

143

(1) положительно однородна первой степени по ценам факторов: c(λw, y) = λc(w, y) y, w W(y);

(2)монотонна по ценам факторов и выпуску при ;

(3)вогнута по ценам на любом выпуклом подмножестве множества W(y);

(4)непрерывна по ценам на внутренности множества W(y), int W(y).

Доказательство:

Доказательство свойств (1), (3) и (4) аналогично приводимым ранее и оставляется читателю в качестве упражнения.

Докажем только монотонность функции издержек.

w′>≠w c(w′, y) > c(w, y) w, w′ W(y).

Пусть r> 0 — оптимальные затраты при ценах факторов w и выпуске y, т.е. wr= c(w, y). Из w′>≠w, следует, что c(w, y) = wr< w′r<c(w′, y).

■

В дальнейшем нам понадобится также понятие функции условного спроса.

Определение 6.

Функция условного спроса на факторы производства r(w, y) есть оптимальное решение Задачи 4 при выпуске y и ценах факторов w.

Заметим, что функция издержек и функция условного спроса на факторы производства определены для любого непустого замкнутого технологического множества Y.

Теорема 15. (Свойства функции условного спроса на факторы)

1)Функция условного спроса на факторы производства r(w, y) однородна нулевой степени как функция цен факторов производства w.

2)Если множество V(y) строго выпукло, то r(w, y) — однозначная непрерывная функция w.

Доказательство:

Доказательство этого утверждения аналогично приводимым ранее и оставляется читателю в качестве упражнения.

■

Если, кроме того, функция издержек дифференцируема, то верна лемма Шеппарда, которая связывает издержки и функцию условного спроса на факторы.

Теорема 16.

Пусть функция издержек дифференцируема по ценам факторов при объеме производства y.

Тогда для всех w int W(y) выполнено

∂c(w, y)

∂wi = ri(w, y)

или

143

144

wc(w, y) = r(w, y).

Доказательство:

Зафиксируем цены факторов на уровне w~ int W(y). Введем функцию на W(y):

γ(w) = c(w, y) – wr(w~, y).

По определению функции издержек и функции условного спроса γ(w) достигает максимума, равного нулю, в точке w~:

γ(w) <0 и γ(w~) = 0.

Если функция издержек дифференцируема по ценам факторов, то функция γ( ) тоже дифференцируема. Поскольку точка w~ внутренняя в W(y), то по условию первого порядка максимума градиент ее должен быть равен нулю:

γ(w~) = wc(w~, y) – r(w~, y) = 0.

■

Как было указано выше, использование функции издержек позволяет рассматривать максимизацию прибыли как двухэтапную процедуру. На первом этапе по данной технологии и соответствующему множеству требуемых затрат строится функция издержек. На втором этапе решается задача выбора объема производства, максимизирующего прибыль, которая в этом случае рассчитывается как разница между выручкой и издержками:

py– c(w, y) →min y Yo .

Здесь через p мы обозначили цены продукции, а через Yo — те объемы производства, которые допустимы при данном технологическом множестве (существуют затраты, которые вместе с y составляют допустимую технологию):

Yo = {y| r: (–r, y) Y}.

Это один из вариантов записи задачи производителя. Если функция издержек дифференцируема, и решение рассматриваемой задачи, y-, является внутренним (т.е. y- int Yo), то оно характеризуется следующим условием первого порядка:

∂ - c(w, y)

∂yk = pk k,

или, в векторной записи,

yc(w, y-) = p.

Таким образом, оптимальный выпуск характеризуется тем, что предельные издержки равны цене.

На основе решения рассматриваемой задачи можно построить

предложения. Она указывает оптимальный объем выпуска y- как функцию цен продукции p и цен факторов w.

Обычно функции издержек используют в моделях частного равновесия (моделях квазилинейных экономик).

Восстановление множества требуемых затрат

Построим по функции издержек c(w, y) при некотором фиксированном объеме производства следующее множество:

144

145

Vc(y) = {r| wr>c(w, y) w>0}.

При любом векторе выпуска y это множество является выпуклым по построению. Так как цены неотрицательны, то выполняется также следующее свойство, которое можно называть свойством свободы расходования производственных факторов:

т.е. если r принадлежит множеству Vc(y) и r′>r, то r′ также принадлежит множеству

Vc(y).

Ясно, что множество требуемых затрат V(y) и Vc(y) могут не совпадать, если само исходное множество допустимых затрат V(y) не является выпуклым или монотонным.

Теорема 17.

Пусть V(y) выпуклое и удовлетворяющее свойству свободы расходования (+) множество. Тогда V(y) = Vc(y).

Доказательство:

Доказательство этого утверждения оставляется читателю в качестве упражнения.

■

Отметим, что даже если множества V(y) и Vc(y) не совпадают друг с другом, это различие не существенно с точки зрения описания поведения производителя, поскольку Vc(y) порождает ту же самую функцию издержек, что и V(y).

Теорема 18.

Пусть c*(w, y) — решение задачи wr→min r

r Vc(y).

Тогда c*(w, y) = c(w, y).

Доказательство:

Доказательство этого утверждения оставляется читателю в качестве упражнения.

■

Заметим, что два эти утверждения — аналоги соответствующих результатов относительно связи Y и Yπ , π(p) и π*(p).

Это утверждение обосновывает возможность получения некоторого множества допустимых затрат Vc(y), порождающего функцию издержек c(w, y). Но совпадение Vc(y) и V(y) возможно только в том случае, когда V(y) удовлетворяет предположениям выпуклости и монотонности. Практический способ восстановления V читатель может сконструировать сам.

Задачи

37. Функция c(y, w) = y1/2(w1w2)3/4 является функцией издержек для некоторой технологии

♦Да

♦Нет

145

146

♦ Недостаточно информации

38. Функция c(y, w) = (y + 1/y)(w1w2)1/2 является функцией издержек для некоторой технологии

♦ Да ♦ Нет

♦ Недостаточно информации

39. Функция c(y, w) = y(w1 – (w1w2)1/2 + w2) является функцией издержек для некоторой технологии

♦ Да ♦ Нет

♦ Недостаточно информации

40. Функция c(y, w) = y(w1 + w2) является функцией издержек для некоторой технологии ♦ Да ♦ Нет

♦ Недостаточно информации

41. Функция c(y, w) = y min{w1, w2} является функцией издержек для некоторой технологии

♦ Да ♦ Нет

♦ Недостаточно информации

42. Функция c(y, w) = y(aw1 + bw2) является функцией издержек для некоторой технологии ♦ при положительных коэффициентах a и b;

♦ если a равно b;

♦ при любых коэффициентах a и b данная функция не является функцией издержек для некоторой технологии

43. Функция c(y, w) = y min{aw1, bw2} является функцией издержек для некоторой технологии

♦при положительных коэффициентах a и b;

♦если a равно b;

♦при любых коэффициентах a и b данная функция не является функцией издержек для некоторой технологии

146

147

44.Функция c(y, w) = ywa1wb2 является функцией издержек для некоторой технологии ♦ если сумма a + b меньше или равна единицы

♦ при положительных коэффициентах a и b, и если сумма a + b меньше или равна единице ♦ при положительных коэффициентах a и b, и если сумма a + b больше единицы

45.Множество требуемых ресурсов на производство объема y задается неравенством

ar1 + br2 >y2 при a, b > 0.

Какой вид имеет соответствующая производственная функция? Постройте функцию издержек.

46. Найдите функции издержек для следующих производственных функций:

а) f(r) = Çi rαi i, αi > 0,

б) f(r) = Ûi airρi ,

в) f(r) = min{ri/ai},

г) f(r) = Ûi airi.

47. Предположим, что предприятие имеет строго вогнутую производственную функцию f(r). Рассмотрим следующие две задачи:

I. Пусть r* является решением первой задачи. Тогда r* является решением второй задачи при c* = wr*.

II. Пусть r* является решением второй задачи. Тогда r* является решением первой задачи при y* = f(r*).

48. Предположим, что предприятие со строго вогнутой производственной функцией f(r) имеет функцию издержек c(w, y). Докажите, что оптимальный объем производства в следующих двух задачах совпадает

py – wr→max y,r py – c(w, y) →max r y <f(r)

49.Доказать, что если функция издержек выпукла, то производителю выгоднее производить продукцию, чем закрыться (производить нулевой объем).

50.Докажите Теорему 13.

147

148

51.Докажите Теорему 14.

52.Докажите Теорему 15.

53.Докажите Теорему 17.

54.Докажите Теорему 18.

55.Пусть функция издержек строго вогнута, и, кроме того, c(0) = 0. Докажите, что данная функция издержек была порождена производственной функцией, которая в точках оптимального выбора производителя характеризуется возрастающей отдачей от масштаба.

56.Для технологии, описываемой производственной функцией f(r) = rα, вычислите функцию издержек. Покажите, что функция издержек однородна по цене фактора производства и выпукла по выпуску y.

57.Показать, что если производственная функция квазивогнута и обладает постоянной отдачей от масштаба, то функция предельных издержек не убывает по выпуску.

58.Покажите, что издержки фирмы возрастут, если цены на все выпускаемые этой фирмой продукты увеличатся пропорционально.

59.Покажите, что если производственная функция строго вогнута, то функция издержек строго выпукла.

Агрегирование в производстве

Пусть существует n фирм с технологическими множествами Yj, j = 1, ..., n. Зададимся вопросом о том, можно ли найти технологическое множество YΣ, такое чтобы производитель с таким технологическим множеством (репрезентативный производитель или агрегированный производитель) демонстрировал определенном смысле такое же поведение, как и n исходных производителей.

Оказывается, что такое технологическое множество построить очень просто:

YΣ = Ûj Yj,

т.е.

YΣ = {Ûj yj | yj Yj}.

Теорема 19.

(1) Если при ценах p технология y-j является решением задачи j-го производителя, то технология

y-Σ = Ûj y-j

148

149

является решением задачи агрегированного производителя при тех же ценах.

(2) Обратно, если y-Σ является решением задачи агрегированного производителя, то найдутся технологии y-j, каждая из которых является решением задачи соответствующего производителя.

Доказательство:

Доказательство оставляется читателю в качестве упражнения.

■

Как следствие указанного свойства, между функциями прибыли существует следующая связь:

πΣ(p) = Ûj πj(p).

Если fj( ) — производственная функция j-й фирмы, то агрегированная фирма будет иметь производственную функцию fΣ( ), которая получается как значение следующей задачи:

Ûj fj(rj) → max {rj Rj}

Ûj rj = rΣ.

Можно показать, что построенная таким образом функция fΣ( ) будет производственной функции, соответствующей агрегированному технологическому множеству YΣ.

Аналогично, если cj( ) — функция издержек j-й фирмы, то агрегированная фирма будет иметь функцию издержек cΣ( ), которая получается как значение следующей задачи:

Ûj cj(w, yj) → max

{yj Yjo} Ûj yj = yΣ.

Задачи

60.Докажите Теорему 19.

61.Докажите, что приведенный в этом параграфе способ агрегирования производственных функций корректен.

62.Докажите, что приведенный в этом параграфе способ агрегирования функций издержек корректен.

63.Технологические множества n фирм одинаковы и состоят из двух технологий, (0; 0) и (–1; 1). Опишите агрегированное технологическое множество YΣ. Покажите, что усредненное технологическое множество YΣ/n в пределе заполняет весь отрезок между (0; 0) и

(–1; 1).

64. Повторите анализ предыдущей задачи для ситуации, когда технологические множества дополнены свободой расходования.

149

150

65. Технологические множества n фирм одинаковы и заданы неравенствами

(yj1 + 1)2 + (yj2 + 1)2 <2, j = 1, ..., n.

Найдите неравенство, задающее соответствующее агрегированное технологическое множество.

66. Технологические множества n фирм одинаковы и заданы неравенствами

yj1 + y2j2 <0, j = 1, ..., n.

Найдите неравенство, задающее соответствующее агрегированное технологическое множество.

67. Для следующих производственных функций, j = 1, ..., n, найдите агрегированную производственную функцию:

а) fj(r) = αj r,

б) fj(r) = αj ln(r + 1), в) fj(r) = αj r,

г) fj(r) = αj(1 – exp( – r)),

68. Для следующих функций издержек, j = 1, ..., n, найдите агрегированную функцию издержек:

а) cj(w, y) = wαj y,

б) cj(w, y) = wαj(exp(y) – 1), в) cj(w, y) = wαj y3,

г) cj(w, y) = –wαj ln(1 – y),

69.Фирма имеет n заводов, издержки производства которых описываются следующими функциями: ci(w, y) = w αi y2, i = 1, ..., n. Определите функцию издержек фирмы.

70.Фирма имеет два завода, издержки производства которых описываются следующими функциями c1(w, y) = w αy2 , c2(y) = w βy. Определите функцию издержек фирмы.

ДВОЙСТВЕННОСТЬ МЕЖДУ ИЗОКОСТАМИ И ИЗОКВАНТАМИ

В заключение укажем на связь между двумя типами кривых: изоквантами в пространстве возможных издержек, определяемыми уравнениями типа f(r) = y при разных y и изокостами в пространстве возможных цен, определяемыми формулами типа c(w, y) = const.

Для наглядности рассмотрим случай двух производственных факторов. Тогда при монотонной технологии можно рассматривать изокванту как функцию r2(r1), а изокосту — как функцию w2(w1). Эти зависимости задаются соответствующими соотношениями, определяющими их как неявные функции.

Из определения изокосты имеем

150