Бусыгин

111

(1) Пусть x, y — две альтернативы из X. Ситуация выбора {x, y} должна принадлежать A, так как это двухэлементное подмножество X. Поскольку по определению C({x, y}) не должно быть пустым, то либо x C({x, y}), либо y C({x, y}). То есть либо x }R y, либо y }R x.

(2) Пусть x, y, z — три альтернативы из X, такие что x }R y и y }R z. Ситуация выбора {x, y, z} должна принадлежать A, так как это трехэлементное подмножество X.

Покажем, что x C({x, y, z}). Если y C({x, y, z}), то из аксиомы выбора Хаутеккера следует, что x C({x, y, z}), поскольку x }R y. Аналогично, если z C({x, y, z}), то x C({x, y, z}). Поскольку C({x, y, z}) непусто, то в любом случае x C({x, y, z}). Это влечет за собой, что x }R z.

*

Данное утверждение показывает, что выбор на основе правила выбора, удовлетворяющего аксиоме Хаутеккера, можно «рационализировать» как выбор на основе некоторого отношения предпочтения. Заметим, что, как будет показано ниже, справедливо и обратное.

Если заданы предпочтения }, то правило выбора потребителя, соответствующее этим предпочтениям естественно определить следующим образом:

C}(A) ≡ {x A | x } y y A}.

Теорема 37.

Пусть правило выбора C}(A) соответствует транзитивному нестрогому отношению

предпочтения }. Тогда это правило выбора удовлетворяет аксиоме выбора Хаутеккера.

Доказательство:

Пусть x }R y. Это означает, что в некоторой ситуации выбора A как x, так и y можно было выбрать (x, y A) и среди выбранных альтернатив была альтернатива x (x C}(A)). По-

скольку правило C}(A) порождено нестрогим отношением предпочтения }, то x } y. Пусть в некоторой другой ситуации выбора A′ как x, так и y можно было выбрать (x, y A′) и среди выбранных альтернатив была альтернатива y (y C}(A′)). Это означает, что y } z

z A′. Из транзитивности следует, что то же самое должно быть верным для x, т.е. x } z

z A′. Таким образом, x C}(A′), то есть аксиома Хаутеккера выполнена. *

Покажем теперь, что если множество ситуаций выбора, на котором определено правило выбора, достаточно богато, то подход, берущий за основу правило выбора, эквивалентен подходу, берущему за основу предпочтения.

Теорема 38.

Пусть выполнены условия предыдущей теоремы. Тогда правило выбора CR(A), порожденное нестрогим отношением выявленного предпочтения }R, сопадает с исходным правилом выбора на A, т.е.

CR(A) = C(A) A A.

Доказательство: (C(A) CR(A))

111

112

Пусть x C(A). Тогда по определению нестрогого выявленного предпочтения x }R y y A. Отсюда видно, что x CR(A).

(CR(A) C(A))

Пусть x CR(A). Поскольку множество C(A) непусто, то существует альтернатива y C(A). Условие x CR(A) означает, что для произвольной альтернативы z A, в том числе и для y, выполнено x }R z, то есть существует такая ситуация выбора A′, что x , y A′ и x C(A′).

Таким образом, мы имеем x , y A′, x , y A, x C(A′) и y C(A). По аксиоме Хаутеккера это означает, что x C(A).

*

Задачи

139.Нестрогое отношение выявленного предпочтения всегда обладает свойством ♦ полноты; ♦ транзитивности;

♦ рефлексивности.

140.Пусть множество альтернатив X конечно. Тогда функция выбора C(.), определенная на всех подмножествах множества X, удовлетворяет аксиоме выявленных предпочтений Хаутеккера, если

♦правило (функция) выбора является вогнутым;

♦выбор участника может быть описан полным и транзитивным отношением предпочтения;

♦функция спроса участника может быть получена на основе сравнения потребительских излишков.

141. Множество альтернатив X конечно и состоит из 3 элементов X = {x, y, z}.

Участник осуществляет свой выбор на его подмножествах A 1={x, y}, A 2={x, y, z}. Выбор участника описывается функцией выбора C(.). Какие из нижеприведенных правил выбора не удовлетворяют аксиоме выявленных предпочтений?

142. Множество альтернатив X конечно и состоит из 3-х элементов X = {x, y, z}. Участник осуществляет свой выбор на его подмножествах A1={x, y}, A 2={y, z},

A3={x, z}. Выбор участника описывается функцией выбора C(.), при этом C(A 1) = {x}, C(A 2) = {y}, C(A 3) = {z}. Какие из нижеприведенных высказываний справедливы?

1)Выбор удовлетворяет аксиоме выявленных предпочтений.

2)Выбор участника представим некоторым отношением предпочтения.

112

113

143. Какому из перечисленных утверждений эквивалентна аксиома выявленных предпочтений?

♦Пусть X — множество альтернатив. Пусть A, A′ X и кроме того x, y A и x, y A′. Тогда из того, что x C(A) и y C(A′) следует x, y C(A) и x, y C(A′), где C(.) — функция выбора.

♦Пусть X — множество альтернатив. Тогда из того, что x A и y A′ следует x A′ и yA, где A, A′ X некоторые подмножества X.

♦Пусть X — множество альтернатив. Пусть A, A′ X и кроме того x C(A) и y C(A′), где C(.) — функция выбора. Тогда x, y A и x, y A′.

144.Отношение выявленного предпочтения обладает свойством полноты, если… ♦ правило выбора задано на множестве всех подмножеств множества альтернатив; ♦ отношение выявленного предпочтения отрицательно транзитивно;

♦ отношение выявленного отношения удовлетворяет аксиоме выявленных предпочтений.

145.Пусть множество альтернатив X конечно и состоит из 3-х элементов X={x, y, z}.

Участник осуществляет свой выбор на его подмножествах A1 = {x, y}, A2={x, y, z}. Выбор участника описывается функцией выбора C(.).

Отношение выявленного предпочтения заданное для данной ситуации

♦не будет удовлетворять аксиоме выявленных предпочтений;

♦не будет полным;

♦будет обладать свойством транзитивности.

146. Одно из необходимых условий для того, чтобы отношение выявленного предпочтения было транзитивно состоит в том, что

♦правило выбора непрерывно;

♦отношение выявленного предпочтения рефлексивно;

♦правило выбора задается на всех трехэлементных подмножествах множества альтернатив.

147. Пусть функция С}(.) сопоставляет каждому непустому подмножеству А множества Х совокупность его наилучших по } элементов

(С}(А) ≡ (х А | не существует y A, такой, что y } x).

Покажите, что если нестрогое и строгое отношения предпочтения связаны соотношением x } y x } y, но не y } x,

то построенные на их основе правила выбора совпадут, то есть область определения A у них будет одинаковой и

С}(А) = С}(А) А A.

113

114

148. Пусть множество альтернатив Х конечно, определенное на нем отношение предпочтения } антисимметрично и отрицательно транзитивно, а функция С(.) сопоставляет каждому непустому подмножеству А множества Х совокупность его наилучших по } элементов

(С}(А) ≡ (х А | не существует y A, такой, что y } x). Покажите, что

(1)для всякого А множество С}(А) не пусто, а функция С}(А) удовлетворяет аксиоме выявленных предпочтений Хаутеккера;

(2)если С(А) А — произвольная функция выбора, сопоставляющая каждому непустому подмножеству А непустое подмножество его элементов и удовлетворяющая аксиоме выбора Хаутеккера, то существует антисимметричное и отрицательно транзитивное отноше-

ние предпочтения }, такое что С(А) = С} (А).

Альтернативный подход к описанию предпочтений: стохастические предпочтения

До сих пор мы смотрели на предпочтения как на детерминированный объект. Условно говоря, наш потребитель всегда предпочитал что-то одно либо яблоки, либо груши. Но реальный выбор экономических агентов далеко не столь однозначно определен. Довольно правдоподобно, что, например, в половине случаев потребитель предпочитает яблоки, а во второй половине груши. Как корректно объяснить такое поведение агентов? Излагаемый далее пример иллюстрирует этот стохастический взгляд на предпочтения.

Пусть потребительское множество X={x, y, z}. Множество ситуаций выбора A={{x, y}, {y, z}, {z, x}}. С(A) – стохастическая функция выбора, которая представляет собой вероятностное распределение над элементами из A и интерпретируется, как вероятность выбора соответствующей альтернативы. Будем говорить, что стохастическая функция выбора С(.) рационализируется предпочтениями, если найдется вероятностное распределение над строгими отношениями предпочтения на X согласующееся со стохастической функцией выбора. Покажем, например, что стохастическая функция выбора C({x, y})= C({y,

Сопоставим с каждым из этих отношений предпочтения вероятность того, что выбор потребителя подчинен этому отношению предпочтения. С учетом этих вероятностей

C({x, y})= (p2+p3+p6, p1+p4+p5), C({y, z})= (p1+p3+p5, p2+p4+p6),

C({z, x})= (p3+p5+p6, p1+p2+p4).

Для ответа на поставленный вопрос необходимо определить найдутся ли такие вероятности (p1, p2, …, p6) которые согласуются с нашей функцией выбора

114

115

1 1 C({x, y})= C({y, z})=C({z, x})=(2, 2).

Фактически необходимо решить следующую систему линейных уравнений:

Легко заметить что решение данной системы уравнений существует, например, возьмем

Аналогично непосредственной проверкой устанавливается, что для случая C({x, y})=

1 3

C({y, z})=C({z, x})=(4, 4) таких вероятностей подобрать не удается, так как не существу-

ет неотрицательного решения соответствующей системы. Наконец проинтепретируем

1 1

полученные вероятности. Функция выбора C({x, y})= C({y, z})=C({z, x})=(2, 2) могла

наблюдатся в действительности если, например, в первом квартале потребитель имел предпочтения y } z } x, во втором квартале он имел предпочтения z } x } y, а в третьем и четвертом y } x } z и x } z } y, соответственно. Тогда его опрос о предпочтениях в течении прошедшего года мог дать подобную функцию выбора.

Агрегирование предпочтений

В этом параграфе мы рассмотрим условия, при которых функция рыночного спроса может быть порождена как решение задачи индивидуальной рациональности отдельного репрезентативного агента. Такого рода конструкции, когда рыночный спрос представляется порождаемым некоторым виртуальным агентом, является рабочим аппаратом современной макроэкономики и поэтому такая постановка вопроса интересна, осмысленна и является одним из базовых оправданий микрооснований макроэкономики.

Предположим, что в экономике присутствуют n агентов, каждый из которых имеет функцию спроса xi(p, Ri). Как не сложно заметить, совокупный спрос этих агентов Ûxi(p, Ri), вообще говоря, зависит от распределения доходов между ними. Пусть потребители в экономике имеют доходы (R1,…, Rn) и предположим, что доходы каждого из потребителей изменились на дифференциально малую величину dRi, причем Û dRi=0. Изменение суммарного спроса в экономике в результате этого изменения доходов составит: Û

d x (p, R )

di Ri i dRi. В случае если суммарный спрос не зависит от распределения доходов, т.е. Ûxi(p, Ri) = x (p, Û Ri) это изменение совокупного спроса должно быть равно 0, т.е. Û

115

116

Следующая теорема дает необходимые и достаточные условия для выполнения этого условия ”всюду” и соответственно для глобального агрегирования предпочтений.

Теорема 39.

Рыночный спрос Û xi(p, Ri) не зависит от распределения доходов потребителей, т.е. Û xi(p, Ri) = x(p, ÛRi) тогда и только тогда, когда индивидуальные функции спроса порождены одним и тем же гомотетичным отношением предпочтения }.

Доказательство:

Предположим, что каждая индивидуальная функция спроса xi(p, Ri) получена на основе некоторого (но одного и того же!) гомотетичного отношения предпочтения }. Как было показано выше, в случае гомотетичных предпочтений индивидуальная функция спроса будет положительно однородна первой степени по доходу. Таким образом, Ûx (p, Ri)=Û

Rix (p, 1)=(ÛRi)x (p, 1)= x (p, Û Ri).

Предположим теперь, что существует некоторая функция спроса x (., .), такая что Ûxi(p, Ri) = x(p, ÛRi) для всех p, R1,…, Rn. Рассмотрим некоторого агента i и распределение доходов Ri = R, и Rj =0, при j≠i. Тогда x(p, R)= xi(p, R), откуда следует, что все агенты одинаковы и имеют одни и те же предпочтения. Для того, что бы показать, что спрос x (.,

.), получен исходя из гомотетичных предпочтений, покажем, что функция x (., .) линейна по R. Это, например, следует из того факта, что x (p, R1+R2)= x (p, R1)+ x (p, R2).

*

Если отказаться от требования, что суммарный спрос всюду не зависит от распределения дохода, а требовать это свойство только локально, то класс предпочтений позволяющих локальное агрегирование расширится.

Одним из важных классов функций полезности позволяющих локальное агрегирование является класс квазилинейных функций полезности. Подробнее этот вопрос мы рассмотрим при рассмотрении квазилинейной экономики.

116

117

2. Поведение производителя

Технологическое множество и его свойства

Рассмотрим экономику с l благами. Для конкретной фирмы естественно рассматривать часть из этих товаров как факторы производства и часть — как выпускаемую продукцию. Следует оговориться, что такое деление довольно условно, так как фирма обладает достаточной свободой в выборе ассортимента производимой продукции и структуры затрат. При описании технологии будем различить выпуск и затраты, представляя последние как выпуск со знаком минус. Для удобства представления технологии продукцию, которая и не затрачивается и не выпускается фирмой, будем относить к ее выпуску, причем объем производства этой продукции считаем равным 0. В принципе не исключена ситуация, в которой продукт, производимый фирмой, также потребляется ею в процессе производства. В этом случае мы будем рассматривать только чистый выпуск данного продукта, т.е. его выпуск минус затраты.

Пусть число факторов производства равно n, а число видов выпускаемой продукции равно m, так что l = m + n. Обозначим вектор затрат (по абсолютной величине) через r Ên+, а объемы выпусков черезy Êm+ . Вектор (–r, yo) будем называть вектором чистых выпусков. Совокупность всех технологически допустимых векторов чистых выпусков y= (– r, yo) составляет технологическое множество Y. Таким образом, в рассматриваемом случае любое технологическое множество — это подмножество Ên– ×Êm+ .

Такое описание производства носит общий характер. При этом можно не придерживаться жесткого деления благ на продукты и факторы производства: одно и то же благо может при одной технологии затрачиваться, а при другой — производится. В этом случае Y Êl.

Опишем свойства технологических множеств, в терминах которых обычно дается описание конкретных классов технологий.

1. Непустота

Технологическое множество Y непусто.

Это свойство означает принципиальную возможность осуществления производственной деятельности.

2. Замкнутость

Технологическое множество Y замкнуто.

Это свойство скорее техническое; оно означает, что технологическое множество содержит свою границу, и предел любой последовательности технологически допустимых векторов чистого выпуска также является технологически допустимым вектором чистых выпусков.

3. Свобода расходования:

если y Y и y′<y, то y′ Y.

Это свойство можно интерпретировать как наличие возможности производить тот же самый объем выпуска, но посредством больших затрат, или меньший выпуск при тех же затратах.

4. Отсутствие «рога изобилия» (“no free lunch”)

y Y и y>0 y= 0

117

118

Это свойство означает что для производства продукции в положительном количестве необходимы затраты в ненулевом объеме.

y2

Y

y1

5. Невозрастающая отдача от масштаба:

если y Y и y′= λy, где 0 < λ < 1, тогда y′ Y.

Рисунок 17. Технологическое множество с возрастающей отдачей от масштаба.

Иногда это свойство называют (не совсем точно) убывающей отдачей от масштаба. В случае двух благ, когда одно затрачивается, а другое производится, убывающая отдача означает, что (максимально возможная) средняя производительность затрачиваемого фактора не возрастает. Если за час вы можете решить в лучшем случае 5 однотипных задач по микроэкономике, то за два часа в условиях убывающей отдачи вы не смогли бы решить более 10 таких задач.

5′. Неубывающая отдача от масштаба:

если y Y и y′= λy, где λ> 1, тогда y′ Y.

В случае двух товаров, когда один затрачивается, а другой производится, возрастающая отдача означает, что (максимально возможная) средняя производительность затрачиваемого фактора не убывает.

5′′. Постоянная отдача от масштаба — ситуация, когда технологической множества удовлетворяет условиям 5 и 5′ одновременно, т.е.

если y Y и y′= λy′, тогда y′ Y λ> 0.

Геометрически постоянная отдача от масштаба означает, что Y является конусом (возможно, не содержащим 0) .

В случае двух товаров, когда один затрачивается, а другой производится, постоянная отдача означает, что средняя производительность затрачиваемого фактора не меняется при изменении объема производства.

y2

Y

y1

Рисунок 18. Выпуклое технологическое множество с убывающей отдачей от масштаба.

6. Выпуклость:

если y′, y″ Y и 0 < α<1, то αy′+ (1 – α)y″ Y.

118

119

Свойство выпуклости означает возможность «смешивать» технологии в любой пропорции.

7. Необратимость

y Y и y≠0 (–y) Y.

Пусть из килограмма стали можно произвести 5 подшипников. Необратимость означает, что невозможно произвести из 5-ти подшипников килограмм стали.

8. Аддитивность

y Y и y′ Y y+ y′ Y.

Свойство аддитивности означает возможность комбинировать технологии. 9. Допустимость бездеятельности:

0 Y.

Теорема 1.

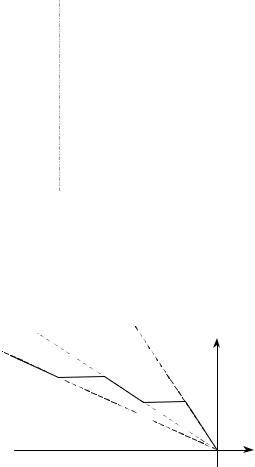
1)Из невозрастающей отдачи от масштаба и аддитивности технологического множества следует его выпуклость.

2)Из выпуклости технологического множества и допустимости бездеятельности следует невозрастающая отдача от масштаба. (Обратное не всегда верно: при невозрастающей отдаче технология может быть невыпуклой, см. Рис. 19).

3)Технологическое множество обладает свойствами аддитивности и невозрастающей отдачи от масштаба тогда и только тогда, когда оно — выпуклый конус.

Доказательство:

Доказательство оставляется в качестве упражнения.

Не все допустимые технологии в равной степени важны с экономической точки зрения.

Рисунок 19. Невыпуклое технологическое множество с невозрастающей отдачей от масштаба.

Среди допустимых особо выделяются эффективные технологии. Допустимую технологию y принято называть эффективной, если не существует другой (отличной от нее) допустимой технологии y′, такой что y′>y. Очевидно, что такое определение эффективности неявно подразумевает, что все блага являются в определенном смысле желательными. Эффективные технологии составляют эффективную границу технологического множества. При определенных условиях оказывается возможным использовать в анализе эффективную границу вместо всего технологического множества. При этом важно, чтобы для любой допустимой технологии y нашлась эффективная технология y′, такая что y′>y. Для

119

120

того, чтобы это условие было выполнено, требуется, чтобы технологическое множество было замкнутым, и чтобы в пределах технологического множества невозможно было увеличивать до бесконечности выпуск одного блага, не уменьшая при этом выпуск других благ. Можно показать, что если технологическое множество обладает свойством свободы расходования, то эффективная граница однозначно задает соответствующее технологическое множество.

Рисунок 20. Эффективная граница технологического множества

Начальные курсы и курсы промежуточной сложности, при описании поведения производителя, опираются на представление его производственного множества посредством производственной функции. Уместен вопрос, при каких условиях на производственное множество такое представление возможно. Хотя можно дать более широкое определение производственной функции, однако здесь и далее мы будем говорить только об «однопродуктовых» технологиях, т.е. m = 1.

Пусть R — проекция технологического множества Y на пространство векторов затрат, т.е.

R = {r Ên | yo Ê: (–r, yo) Y}.

Определение 1.

Функция f( ): R &Ê называется производственной функцией, представляющей технологию Y, если при каждом r R величина f(r) является значением следующей задачи:

yo →max y

(–r, yo) Y.

Заметим, что любая точка эффективной границы технологического множества имеет вид (–r, f(r)). Обратное верно, если f(r) является возрастающей функцией. В этом случае yo = f(r) является уравнением эффективной границы.

Следующая теорема дает условия, при которых технологическое множество может быть представлено производственной функцией.

Теорема 2.

Пусть для технологического множества Y Ê×(–R) для любого r R множество

F(r) = {yo | (–r, yo) Y}

замкнуто и ограничено сверху. Тогда Y может быть представлено производственной функцией.

Доказательство:

120