Бусыгин

71

e(tp, x) = tp1tp2(u(x))2 = tp1p2(u(x))2 = t e(p, x). tp2+a2tp1 p2+a2p1

Покажем свойство неубывания по ценам. Отметим, что

1

Действительно при росте при росте p1 величина p1 убывает, что в свою очередь влечет

(u(x))2

рост значения дроби 1 a2 , и, тем самым, рост функции расходов. p1 + p2

Покажем теперь вогнутость функции расходов по ценам. Матрица вторых частных про-

Несложно заметить, что первый главный последовательный минор отрицателен, а второй равен 0. То есть, главные последовательные миноры чередуют свой знак, начиная с первого, который отрицателен. Отсюда непосредственно следует, что матрица H отрицательно полуопределена и, соответственно, вогнутость функции e(p, x).

Наконец проверим, что x } y e(p, x)>e(p, y). Действительно, в силу положительности

функции полезности имеем, что e(p, x)>e(p, y) x } y.

Рассмотрим теперь вопрос о взаимосвязи прямой и двойственной задач потребителя. Следующая теорема, называемая теоремой взаимности (двойственности), устанавливает условия совпадения решений прямой и двойственной задач потребителя.

Теорема 19. (Теорема взаимности (двойственности))

Пусть множество допустимых альтернатив X непусто, замкнуто, ограничено снизу, выпукло, 0 X и p ÊK++, а потребитель описывается системой непрерывных неоклассических предпочтений. Тогда

1)если предпочтения локально ненасыщаемы, то x- x(p,R) влечёт x- h(p,x-).

2)для любого -h h(p, x-) и x- X, выполнено -h x(p,e(p,x-)).

Доказательство:

(1) Предположим противное: пусть x- h(p,x-), т.е. в двойственной задаче существует потребительский набор h′}x- такой, что px->ph′. Из локальной ненасыщаемости предпочтений следует, что существует h′′, такой, что h′′}h′}x- и при этом px->ph′′. А это противоречит оптимальности x- в прямой задаче потребителя.

71

72

(2). Предположим, что -h не является решением прямой задачи потребителяпри ценах p и доходе e(p,x-). Тогда существует потребительский набор x′B(p,e(p,x-)) такой, что u(x′) > u(-h). В силу непрерывности отношения предпочтения найдется 0<α<1 такое, что αx′B(p,e(p,x-)) и u(αx′) > u(-h). Это противоречит оптимальности -h в двойственной задаче потребителя.

■

Мы показали, что при выполнении условий данной теоремы, справедливо, что для любого x- x(p,R) выполнено x- h(p,x-). В силу этого, из определения функции расходов имеем e(p, x-)=px-, в силу локальной ненасыщаемости предпочтений справедливо, что px-=R. То есть для любого x- x(p,R) справедливо тождество e(p, x-)=R. Аналогично, пусть -hh(p,x-) при некотором x- X, тогда по доказанной теореме двойственности получаем, что -h x(p,e(p,x-)). В силу оптимальности -h при ценах p и доходе e(p,x-) имеем, что ν(p,e(p,x-))=u(-h). Также заметим, что в силу непрерывности предпочтений u(-h)=u(x-). Таким образом, получаем что ν(p,e(p,x-))= u(x-). Покажем теперь, что x(p, e(p,x-))=h(p,x- ). Включение h(p,x-) x(p,e(p,x-)) доказано в теореме двойственности. Пусть теперь x x(p,e(p,x-)), тогда в силу локальной ненасыщаемости x h(p, x) и e(p, x)=e(p, x~). Так как потребительский набор x допустим при ценах p и доходе e(p,x-) то u(x)> u(x-). Таким образом, несложно увидеть, что h(p, x) h(p,x-), откуда непосредственно вытекает x(p,e(p,x-))=h(p,x-). Из приведенных рассуждений непосредственно следует, что для любого x- x(p,R) выполнено x(p, R)=h(p,x-). Этими рассуждениями мы доказали следующее

Следствие. (Соотношения двойственности)

Пусть выполнены все предположения Теоремы 19. Тогда:

•для любого x- x(p,R) выполнено e(p, x-)=R;

•для любого x- x(p,R) выполнено x(p, R)=h(p,x-);

•ν(p, e(p, x-)) = u(x-);

•x(p, e(p, x-)) = h(p,x-).

Проиллюстрируем важность установленных соотношений двойственности.

Пример 10.

Пусть мы, решив задачу потребителя, нашли функцию спроса и непрямую функцию полезности. Этой информации достаточно для того, чтобы найти функцию хиксианского спроса и функцию расходов, не решая, соответственно, двойственную задачу. Действи-

Пример 11.

72

73

Пусть непрямая функция полезности потребителя имеет вид ν(p, R) = a(p)R и x(p, R) = Rx(p, 1). Тогда используя соотношения двойственности несложно видеть, что e(p, x)

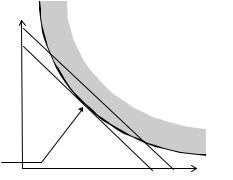
хиксианский

спрос

Рисунок 11. «Толстая» кривая безразличия

Рассмотрим теперь пример когда хиксианский и маршаллианский спрос не совпадают. Для построения этого примера достаточно рассмотреть предпочтения, не обладающие свойством локальной ненасыщаемости. В качестве таковых, рассмотрим предпочтения порождающие “толстую” кривую безразличия (такие кривые безразличия появятся, например, если взять в качестве функции полезности целую часть какой-нибудь “нормальной” функции полезности). Хиксианский спрос всегда будет лежать (случай двух благ) на левой границе “толстой” кривой безразличия. На Рисунке 11 эта граница изображена темной линией. Маршаллианский же спрос может лежать внутри “толстой” кривой безразличия (Найдите его на приведенном Рисунке!).

Вернемся теперь, как и обещали, к обсуждению закона спроса. Используя полученные соотношения двойственности, закон спроса при компенсированном изменении дохода по Хиксу (p′ - p)( h(p′, x-) - h(p, x-)) < 0 можно переформулировать в виде:

(p′ - p)( h(p′, x-) - h(p, x-)) = (p′ - p)( x(p′, e(p′, x-)) - x(p, e(p, x-)))<0.

Пусть x- оптимальное решение задачи потребителя при ценах p и доходе R, тогда данное свойство означает, что (p′ - p)(x(p′, e(p′, x-)) - x(p, R))<0. Сравним теперь два полученных нами варианта закона спроса при компенсированном изменении дохода по Слуцкому и по Хиксу:

1)(p′ – p)(x(p′, p′x-)) - x(p, R)) < 0;

2)(p′ - p)(x(p′, e(p′, x-)) - x(p, R)) < 0.

Единственное отличие этих свойств состоит в величине компенсации. В первом случае компенсированное изменение дохода равно ∆1= p′x- – R, а во втором случае величина

компенсации равна ∆2= e(p′, x-) – R. Несложно понять, что ∆1>∆2, действительно ∆1>∆2

p′x- > p′h(p′, x-). Последнее неравенство справедливо, так как потребительский набор x- допустим в двойственной задаче, но он не может стоить меньше чем оптимальный на-

бор h(p′, x-).

73

74

Рисунок 12. Компенсирующие изменения дохода по Слуцкому и Хиксу при

Обе указанные формы компенсированного изменения дохода имеют достаточно ясную графическую интерпретацию. Предположим, что в момент времени 0 цены были p0=(p10, 1), а доход в нулевой момент времени был равен R. В момент времени 1 упала цена перво-

го блага, а цена второго блага и доход остались неизменными, т.е. p1=(p11, 1), p01 > p11. На

рисунке 12 показана разница в определениях компенсирующего изменения дохода по Слуцкому и Хиксу. На левом рисунке показан способ нахождения компенсирующего изменения дохода по Слуцкому. Строим обе бюджетные линии. Находим спрос в начальный момент времени. После чего начинаем двигать новую бюджетную линию до тех пор, пока она не пройдет через точку спроса в начальный момент времени. Разница между дохо-

дом, отвечающим этому положению и исходным доходом, и будет компенсированным изменением по Слуцкому. На втором рисунке показан способ нахождения компенсированного изменения по Хиксу. Отличие от предыдущего случая состоит в том, что в этот раз мы двигаем бюджетную линию до точки касания с исходной кривой безразличия, определяющей спрос потребителя.

Рассмотренные варианты закона спроса при компенсированном изменении дохода позволяют делать некоторые выводы о поведении потребителя при изменении параметров модели. Неоспоримое достоинство этих свойств в том, что они выполняются при очень слабых предположениях на предпочтения индивидуума, но в то же время, это достоинство уравновешивается ограниченностью этих выводов. Мы можем говорить о направлении изменения спроса только при компенсированном изменении дохода. Фактически мы не получаем точной информации в ситуации когда цены изменились, а доход остался неизменным. То есть наша информация дает лишь приблизительный, возможно, достаточно грубый ответ на вопрос о поведении спроса. Этот недостаток не возможно устранить легкой ценой, требуется сделать некоторые дополнительные предположения на свойства функции полезности.

В дальнейшем нам понадобится следующее определение.

Определение 19.

Будем говорить, что функция x(p, R) удовлетворяет закону спроса, если выполнено соотношение

(p′ – p)(x(p′, R)– x(p, R)) < 0.

Отметим очевидное отличие формулировки этого свойства от рассмотренных нами выше. Данное свойство должно выполняться при фиксированном доходе, в отличие от рассмотренных выше свойств, выполнявшихся при компенсированном изменении дохода.

74

75

В случае выполнения закона спроса мы получаем чистую информацию об изменении спроса не обусловленную изменением дохода, что, в частности, позволяет делать выводы об отсутствии товаров Гиффена в экономике, то есть об отсутствии товаров, спрос на которые растет при росте цены. Естественно задаться вопросом об условиях, которые гарантирует выполнение закона спроса. Ответ на этот вопрос дает следующая теорема.

Теорема 20. (Закон спроса)

Пусть X=ÊK+ , p ÊK++, R > 0

1)функция полезности u(x) определена на ÊK+ , вогнута и дважды непрерывно дифференцируема;

2)градиент u(x) неотрицателен и удовлетворяет неравенству u(x)x > 0;

3)матрица вторых частных производных H функции u(x) отрицательно определена.

Тогда, функция спроса x(p,R) удовлетворяет закону спроса тогда и только тогда, когда для любого x ÊK+ выполнено неравенство:

u(x)x xÅHx

u(x)H-1 u(x)Å – u(x)x < 4.

Доказательство:

Доказательство данного утверждения достаточно длинно и технично, заинтересованный читатель сможет его найти в работах: Митюшин Л.Г., Полтерович В.М., Критерий монотонности функций спроса, Экономика и математические методы, Т. 14(1), 1978 и Полте-

рович В.М., Экономическое равновесие и хозяйственный механизм, М., Наука, 1990, стр. 69-77. Некоторый вариант этой теоремы в терминах непрямой функции полезности можно найти в Quah, J. K.-H., The weak axiom and comparative statics, Oxford University, Discussion paper, 1999.

■

Отметим, что, несмотря на силу заключения данной теоремы, она мало применима, так как прямая проверка выполнения сформулированного неравенства даже в случае двух товаров достаточно утомительна, а в пространствах большей размерности вряд ли представляется возможной. Но она служит полезным источником для получения достаточных условий выполнения закона спроса. В рамках сделанных предположений, первое слагаемое отрицательно, поэтому закон спроса будет заведомо выполнен в случае справедливости неравенства:

xÅHx

– u(x)x < 4.

В этом параграфе мы рассмотрели прямую и двойственную задачи потребителя, изучили их свойства и рассмотрели некоторые основные соотношения связывающие эти задачи. В следующем параграфе мы продолжим рассмотрение основных свойств данных задач, используя аппарат дифференциального исчисления.

Задачи

71. Для каждой из нижеприведенных функций найти маршаллианскую функцию спроса, непрямую функцию полезности, хиксианскую функцию спроса, функцию расходов. Проиллюстрируйте соотношения двойственности между маршаллианской и хиксианской функциями спроса, а также между непрямой функцией полезности и функцией расходов.

a) u(x)=x1+ x2;

75

76

b)u(x)= x1 + x2;

c)u(x)= x1 + x2;

d)u(x)=x1x2;

2

e) u(x)= ln(x1)+x22 ;

f) u(x)= x1x2 ; x1+ x2

g)u(x)= x21 +x22 ;

h)u(x)=min{ x1, x2};

i)u(x)=max{ x1, x2};

j)u(x)=min{ 2x1– x2, 2x2– x1};

k)u(x)=28x1+28x2–2x21 –3x1x2–2x22

l)u(x)= x21 +x22 +4x1+4x2+2x1x2+6.

Основываясь на полученных результатах, проверьте теоретические свойства маршаллианской функции спроса, непрямой функции полезности, хиксианской функции спроса, функции расходов.

72. Приведите пример функции полезности, для которой:

•Доля средств, расходуемых потребителем на приобретение каждого блага — постоянная (и положительная) доля совокупных расходов потребителя.

•Спрос потребителя на любое благо зависит лишь от относительной цены данного блага и совокупных потребительских расходов.

•Спрос потребителя на первые l–1 благ зависит лишь от относительной цены этих благ.

•Спрос потребителя на первые l–1 благо зависит лишь от цены данного блага.

•Структура спроса потребителя постоянна (отношение величины покупок j блага к величине 1 блага, j=1,..., l).

•Отображение спроса не является выпуклым множеством.

73.Покажите, что если функция полезности является квазилинейной, то непрямая функция полезности v(p,R) имеет вид v(p,R) = a(p) + b(p)R для тех значений p и R, при которых оптимальный потребительский набор содержит все блага (в положительных количествах).

74.Покажите, что если функция полезности потребителя однородна, то отношение функций спроса на любые два товара не зависит от уровня дохода.

75.Пусть полезность потребителя зависит от двух благ, и первое благо является дискретным (доступные уровни его потребления — целые числа), а потребитель имеет квазилинейные предпочтения. При каких ценах на благо 1 потребитель предъявляет спрос на него на уровне 1, 2, …?

76

77

76.Покажите, что если функция полезности квазилинейна, то непрямая функция полезности — выпуклая функция цен.

77.Покажите, что если функция полезности квазилинейна, причем l-ое благо входит линейно, то хиксианский спрос на первые l–1 благо не зависит от U. Каков вид функции расходов в этом случае? При каких предположениях справедливы вышеприведенные утверждения?

78.Докажите теорему 17.

79.Пусть все исходные данные те же что и в примере 8. Укажите геометрическое место точек, среди которых может находиться спрос потребителя, обладающего квазилинейными предпочтениями.

80.(Алипрантис, Браун, Беркеншо) Рассмотрите функцию полезности вида u(x, y) = x + y+y+z/(1+z).

(а) Покажите, что функция полезности строго монотонна, строго вогнута и непрерывна.

(б) Покажите, что если (x, y, z) Ê 3+ и z>0, то (x, y+ z, 0) } (x, y, z). (в) Пусть p>>0 и p2 = p3. Покажите, что для вектора спроса выполнено равенство z(p,R)=0.

(г) Рассмотрите последовательность цен pn=(1, 1/n, 1/n) чему равны пределы z(pn,R) и y(pn,R).

81.В случае, когда в экономике наличествуют всего 2 товара, найдите, если это возможно,

маршаллианский, хиксианский спросы, непрямую функцию полезности и функцию расходов для потребителя, описываемого лексикографическими предпочтениями.

82.Сформулируйте и докажите аналоги теорем 14 – 19 для случая когда доход потребителя формируется за счет продажи начальных запасов w.

83.Сформулируйте и докажите аналоги теорем 14 – 19 для случая когда доход потребителя формируется за счет заработной платы. Почасовая ставка заработной платы равна w, потребитель располагает 24 часами времени в сутки. Время отдыха является одним из благ, количество потребления которого выбирает потребитель.

84.(МасКолелл, Винстон, Грин) Рассмотрите следующую функцию расходов

e(p, x) = exp{Σαlln(pl) + (Πpβll)u(x)}.

При каких ограничениях на параметры αl, βl данная функция является функцией расходов? С учетом ответа на первый вопрос найдите отвечающую ей непрямую функцию полезности.

77

78

85.Пусть непрямая функция полезности имеет вид a(p) + b(p)R. Какими свойствами должны обладать функции a(p) и b(p) для того чтобы данная функция была непрямой функцией полезности рационального потребителя.

86.В экономике присутствует два товара. Потребитель имеет локально ненасыщаемые

компенсирующее изменение дохода по Слуцкому приp=(1, 1), p′=(1, 4) и R=121.

87. Пусть непрямая функция полезности некоторого потребителя имеет вид: ν(p, R) =

R

min{p1, p2} . Найдите компенсирующее изменение дохода по Хиксу при p=(1, 1), p′=(1, 4)

и R=121.

88.Функция полезности называется псевдовогнутой, если из условия u(x)(y – x) < 0, следует, что u(y)< u(x). Покажите, что если функция полезности является псевдовогнутой, то условия Куна-Таккера являются достаточными условиями для нахождения решения задачи потребителя. Покажите, что любая вогнутая функция является псевдовогнутой, а любая псевдовогнутая функция является квазивогнутой.

89.Пусть функция полезности равна u(x) = (x1+x2–2)3. Цена на первый товар равна 1, а на второй равен 2. Доход потребителя равен 3. Проверьте, что целевая функция квазивогнута и локально ненасыщаема. Покажите, что точка (1, 1) удовлетворяет условиям КунаТаккера, но не является оптимальной.

функции полезности и вычислите на ее основе функцию затрат и функции спроса (маршаллианского и хиксианского).

92.Проверьте выполнение соотношений двойственности (взаимности) в случае если пове-

дение потребителя описывается функцией полезности: u(x) =[x1x2], где [.] – оператор взятия целой части.

93.Пусть потребитель имеет однородную первой степени функцию полезности при ценах p=(1, 1) и доходе R=5 его функция спроса была равна x(p, R) = (2, 3). Определите геометрическое место точек, которые могут представлять спрос потребителя, если на покупку первого товара ввели налог в размере 20% от цены, а доход потребителя остался неизменным. Ответьте на этот вопрос, в случае если налог на доход потребителя изменился с 20 до 40 процентов.

78

79

94. Пусть функция полезности потребителя аддитивно-сепарабельна, то есть имеет вид:

K

u(x)=Û ui(xi). Запишите достаточные условия оптимальности для задачи потребителя в

i=1

предположении, что потребитель имеет выпуклые, локально ненасыщаемы предпочтения. Покажите, что если u′i(0) = +∞, то потребитель покупает все блага в положительных количествах.

95. Пусть функция полезности потребителя аддитивно-сепарабельна, то есть имеет вид:

K

u(x)=Û ui(xi). Кроме того, предположим, что выполнены все условия теоремы 20 и каж-

i=1

дое слагаемое ui(xi) положительно однородно степени αi >0. Покажите, что спрос данного потребителя удовлетворяет закону спроса.

96. Пусть функция полезности, представляющая некоторое нетранзитивное отношение, имеет вид k(x, y) = y–11/2x1/22 + ln(x3) – x–11/2y1/22 – ln(y3). Найдите маршаллианский спрос данного потребителя. (Для пояснения обозначений смотри теорему 9.)

Дифференциальные свойства задачи потребителя

Перед тем как перейти к рассмотрению дополнительных содержательных свойств решения задачи потребителя, проведем предварительную подготовку и приведем условия гарантирующие дифференцируемость функций спроса, непрямой функции полезности и функции расходов. Эти технические вопросы послужат некоторым обоснованием законности применяемых далее рассуждений.

Теорема 21.

Пусть X=ÊK+ , p ÊK++, R > 0, функция полезности обладает свойствами локальной ненасыщаемости, сильной квазивогнутости, непрерывности и дважды непрерывно дифференцируема. Предположим, что оптимальный потребительский набор строго положителен, x(p,R)>>0. Тогда,

1)функция маршаллианского спроса x(p,R) и непрямая функция полезности ν(p, R) непрерывно дифференцируемы по ценам и доходу;

2)функция хиксианского спроса h(p, x) и функция расходов e(p, x) непрерывно дифференцируемы по ценам.

Доказательство:

Как было показано в предыдущем параграфе, приведенные предположения гарантируют, что условия Куна-Таккера являются необходимыми и достаточными условиями оптимальности для задачи потребителя. Также было показано, что при выполнении этих условий множитель Лагранжа строго положителен. С учетом этого факта и того, что x(p,R)>>0 условия Куна-Таккера (условия первого порядка) которые определяют потребительский спрос как функцию от параметров (p, R) задачи, запишутся следующим образом.

u(x) – λpÅ = 0; px –R =0.

79

80

По теореме о неявной функции42 функция спроса x(p,R) и множитель Лагранжа λ будут непрерывно дифференцируемыми если матрица

является невырожденной, где матрица H(x(p,R)) – матрица вторых частных производных функции полезности, вычисленная в точке спроса. Невырожденность этой матрицы эквивалентна невырожденности матрицы (Почему?)

Покажем, что при сделанных нами предположениях матрица H~ не вырожденная. Предположим противное. Тогда существует такой вектор y и число z, такие, что Hy + u(x)Å z = 0 и u(x)y=0, где (y, z)≠0. Пусть y=0, а z≠0, то u(x) = 0. Это противоречит доказанному ранее свойству существования такого блага i, что ui′(x(p,R)) > 0. Пусть теперь y≠0, тогда yÅHy + yÅ u(x)Åz = yÅHy = 0 и u(x)y=0, что противоречит свойству силь-

ной квазивогнутости. Таким образом, мы доказали, что матрица H~ не вырождена. И, тем самым, функция маршаллианского спроса и множитель Лагранжа λ являются непрерывно дифференцируемыми по ценам и доходу. В силу определения непрямой функции полезности ν(p, R)= u(x(p, R)) и непрерывной дифференцируемости функции полезности и функции спроса имеем непрерывную дифференцируемость непрямой функции полезности по ценам и доходу. В силу свойств взаимности ν(p, e(p, x)) = u(x). С учетом монотонности непрямой функции полезности по доходу и непрерывной дифференцируемости непрямой функции полезности имеем непрерывную дифференцируемость функции расходов по ценам. Наконец, в силу соотношения x(p, e(p, x)) = h(p, x), непрерывной дифференцируемости функции спроса по доходу и непрерывной дифференцируемости функции расходов по ценам имеем непрерывную дифференцируемость хиксианского спроса по ценам.

■

В задачах к этому параграфу читателю предложат доказать непрерывную дифференцируемость функции расходов и хиксианского спроса по x.

При выполнении условия дифференцируемости непрямой функции полезности, функции расходов и функций маршаллианского и хиксианского спросов выполняются три важных свойства теории потребителя: лемма Шепарда, тождество Роя и уравнение Слуцкого.

Связь между функциями расходов и (хиксианского) спроса описывается леммой Шепарда.

Теорема 22. (Лемма Шепарда43)

Пусть решение взаимной (двойственной) задачи внутреннее и выполнены условия теоремы 21, тогда44

∂e(p,x)

∂pi = hi(p, x)

42Смотри, например, Зорич, В.А., Математический анализ I, М., МЦНМО, 2001, стр. 568-69.

43Shephard, R. W., Cost and production function, Princeton, Princeton Univ. Press, 1953

44На самом деле для справедливости данного утверждения достаточно дифференцируемости функции расходов и непрерывности системы неоклассических предпочтений.

80