Бусыгин

221

чае сепарабельной функции полезности существует тогда и только тогда, когда существуют решения задач CQk при любом k = 1, ..., l.)

Введем обозначения 67

Легко видеть, что при любом pk, таком что p < pk < -p, решение задачи CQk существует. Действительно в силу непрерывности функции ∂vik(xik)/∂xik, существует xik, такое что

∂v (x )

ikx ik = pk.

∂ k

Это xik должно быть решением задачи потребителя при ценах pk.

Кроме того, при ценах pk <p задача CQk не имеет решения. Покажем это. Пусть при pk <p

существует решение xik(pk) >0. Тогда должно выполняться необходимое условие оптимума (условие первого порядка)

Так как xik(pk) + ε > 0, мы получили противоречие с определением инфимума. Тем самым, предположив существование решения задачи CQk при pk < p мы пришли к противоречию, а

значит полностью обосновали то, что при pk < p задача CQk не имеет решения.

Покажем теперь, что xik(pk) → 0 при pk → ∞. Рассмотрим для этого два случая: -p = ∞ и -p < ∞.

Пусть -p = ∞. При pk > p, по доказанному ранее решение xik(pk) задачи CQk существует, причем оно будет внутренним (xik(pk) > 0), так как любое значение pk > p по непрерывности функции ∂vik(xik)/∂xik может быть реализовано при соответствующем подборе xik. Это означает, что условие первого порядка в этой задаче выполнено как равенство при pk > p:

67 -p — это так называемая цена «удушения» спроса.

221

222

∂vik(xik(pk)) = p ,

∂xk k

и оно определяет функцию спроса xik(pk) при pk > p.

Рассмотрим теперь последовательность {pnk}, такую что

lim →∞ pn = ∞.

n k

Выделим из последовательности {pkn} возрастающую подпоследовательность {pnks}. На основании подпоследовательности цен {pnks} построим соответствующую ей последовательность объемов спроса {xniks} по правилу

∂vik(xniks) = pns. ∂xik k

Так как lim s→∞ pnks = ∞, то в силу строгой вогнутости функции полезности имеем, что последовательность объемов спроса {xniks} убывает, причем xniks +1< xniks. Как мы отметили выше при pk > p решение задачи CQk является внутренним и, таким образом, xniks > 0 ns, но каждая убывающая и ограниченная снизу последовательность имеет предел. Пусть x~ik — предел этой последовательности объемов спроса и x~ik > 0. Тогда, как нетрудно заметить, подпоследовательность {pnks} имеет (в силу непрерывности ∂vik(xik)/∂xik) конечный предел ∂vik(x~ik)/∂xik, что противоречит ее построению. Получив противоречие, мы доказали, тем самым, что x~ik= 0 и тем самым, что xik(pk) →0 при pk →∞.

Пусть теперь -p < ∞. Тогда в силу убывания функции ∂vik(xik)/∂xik имеет место равенство

Отсюда следует, что при pk >p- спрос на данное благо равен нулю, т.е. xik(pk) = 0, поскольку в силу вогнутости целевой функции это необходимое условие оптимальности является также и достаточным. Отметим, что так как функция полезности в задаче CQk является строго вогнутой, то xik(pk) = 0 — единственное решение этой задачи. Тем самым мы доказали, что в общем случае xik(pk) →0 при pk →∞.

Потребительский излишек: определение, связь с прямой и обратной функциями спроса

Пользуясь выведенными выше характеристиками потребительского выбора, проанализируем связь оценки vi(xi) с площадью под кривой спроса потребителя.

Пусть xi = xi(p), т.е. является спросом потребителя при ценах p. Величина

CSi = vi(xi1,..., xil) – pxi – vi(0)

называется потребительским излишком. В дальнейшем без потери общности будем предполагать, что vi(0) = 0.

Мы рассмотрим случай квазилинейных сепарабельных функций полезности, т.е.

l

vi(xi1,..., xil) = Ûvik(xik). Потребительский излишек при этом получается суммированием

k=1

потребительских излишков, получаемых потребителем на рынках отдельных благ:

222

223

CSi = Û(vik(xik) – pkxik) = ÛCSik,

где CSik = vik(xik) – pkxik.

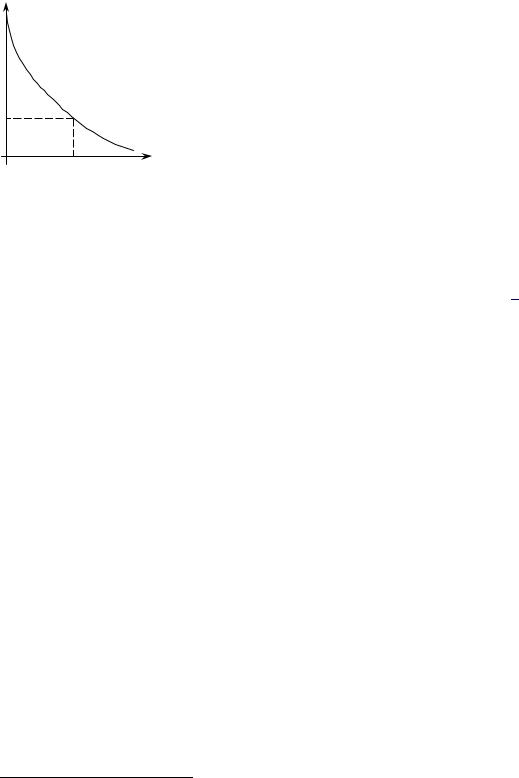
В этом случае геометрически излишек потребителя на рынке k-го блага равен площади фигуры, лежащей под графиком функции обратного спроса выше цены этого блага (см.

Рис. 47).

Рисунок 47. Излишек потребителя

Поясним это. Рассмотрим потребительский излишек как функцию цен:

Функции CSik(pk) = vik(xik(pk)) – pk xik(pk) определены при всех ценах pk > p и, кроме того, не могут быть отрицательными.68

Как было доказано, xik(pk) →0 при pk →∞, откуда vik(xik(pk)) →0 при pk →∞. Поскольку pk xik(pk) <vik(xik(pk)), то при росте цены блага расходы на его приобретение стремятся к

нулю, т.е. pk xik(pk) →0 при pk →∞.

Функция CSi(p) является дифференцируемой, если функция полезности дважды дифференцируема. Дифференцируя ее, получаем (с учетом условий первого порядка для задачи потребителя), что при xik(pk) > 0

(Читателю предоставляется проверить этот факт самостоятельно).

Если xik(t) > 0 при всех t >pk , то проинтегрировав обе части этого дифференциального уравнения, получим

Откуда

∞

CSik(p) – lim t→∞CSik(t) = øxik(t)dt,

p

что позволяет выразить излишек потребителя i от потребления блага k в виде

68 Так как xik = 0 является допустимым в задаче C1k(pk), то CSik(pk) = vik(xik(pk)) – pk xik(pk) > vik(0) – pk 0 = 0, и, тем самым, CSik(pk) > 0.

223

224

∞

CSik(p) = øxik(t)dt + lim t→∞CSik(t).69

p

Поскольку второе слагаемое в этом соотношении равно нулю:

lim t→∞CSik(t) = 0,

то

∞

CSik(p) = øxik(t)dt.

p

В силу того, что функция pik( ) является обратной к функции xik( ), имеет место соотношение70

xik(p)

CSik(p) = ø pik(q)dq – pxik(p),

0

В итоге, общий потребительский излишек получаем суммированием этих интегралов по всем рынкам:

CSi(p) = ÛCSik(p) = Ûøxik(t)dt =

= Û ø pik(t)dt – pÛxik(p).

Характеристика поведения производителей в квазилинейных экономиках

Напомним, что в рассматриваемом случае технологию каждого производителя представляет функция издержек. Если технологическое множество выпукло, то функция издержек является выпуклой. В этом параграфе мы приведем постановки задачи потребителя при различных предположениях о типе конкуренции с которым сталкивается производитель.

Предположим, что j-й производитель сталкивается с функцией обратного спроса на производимые им блага вида

pj = pj(yj).

Здесь мы отходим от предположения о совершенстве конкуренции — производители не рассматривают цены как данные.

В предположении (обычном для неоклассической парадигмы), что производитель выбирает объемы производства соответствующих благ, максимизирующие прибыль, задача j-го производителя имеет вид:

πj = pj(yj)yj – cj(yj) → maxyj > 0.

Если функции p(yj) и cj(yj) дифференцируемы, то необходимое условие оптимальности выпуска yj производителя j имеет вид

224

225

pjk(yj)yj + pjk(yj) – cjk′(yj) <0,

причем если yjk > 0, то

pjk(yj)yj + pk(yj) – c′jk(yj) = 0.

В случае, если функции полезности сепарабельны, спрос на каждое благо зависит только от его цены. В этом случае цена любого блага зависит только от продаваемого количества блага:

pjk = pjk(yjk).

Предположим также, что функция издержек производителя также сепарабельна, т.е.

l

cj(yj) = Ûcjk(yjk).

k=1

В этом случае прибыль имеет вид

l

πj = Û[pjk(yjk)yjk – cjk(yjk)].

k=1

Задача максимизации прибыли распадается, таким образом на l задач. Условия первого порядка приобретают более простой вид:

pjk′(yjk)yjk + pjk(yjk) <cjk′(yjk),

причем при yjk > 0

pjk′(yjk)yjk + pjk(yjk) = cjk′(yjk).

И наконец, если цена спроса не зависит от продаваемого объема блага,

pjk(yjk) = const,

(производители принимают цены как данные, в отрасли складывается ситуация совершенной конкуренции), то pjk′(yjk) = 0 и условия первого порядка приобретают вид

pjk < cjk′(yjk),

причем при yjk > 0

pjk = cjk′(yjk).

Последнее соотношение задает функцию предложения k-го блага j-м предприятием. Это функция зависит только от цены k-го блага.

Излишек производителя

Предположим, что производитель рассматривает цену как данную, или, другими словами, цена спроса не зависит от продаваемого объема, и цены у всех производителей одинаковы и равны p. В качестве излишка производителя при ценах p будем рассматривать его прибыль при этих ценах, т.е.

PSj = πj = pyj – cj(yj).

225

226

pk cjk( )

PS yjk

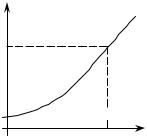
Рисунок 48. Излишек производителя

В случае, если функция издержек сепарабельна, излишек производителя можно представить как сумму излишков по l рынкам:

PSj = Û[pkyjk – cjk(yjk)] = ÛPSjk.

Можно представить излишек производителя на k-м рынке в виде интеграла:

yjk

PSjk = ø [pk – cjk′(t)]dt – cjk(0).

0

Он равен (с точностью до константы cjk(0) ) площади фигуры, образуемой прямой, проходящей через точку (0, pjk) параллельно оси абсцисс, и кривой предельных издержек cjk′(yjk) (кривой предложения). В случае, когда cjk(0) = 0 получаем, что излишек производителя равен

yjk

PSjk = ø [pk – cjk′(t)]dt.

0

Связь излишков потребителя и производителя с индикатором благосостояния

Предположим, что {(x1, z1), ..., (xm, zm), (y1, r1), ..., (yn, rn)} — допустимое состояние экономики, причем (xi, zi) — решение задачи CQ i-го потребителя при ценах p и

pÛxi = pÛyj.

i I j J

Тогда

W(x, y) = Ûvi(xi) – Ûcj(yj) =

i I j J

= Ûvi(xi) – pÛxi + Û(pyj – cj(yj)) = CS + PS,

где

CS = ÛCSi

i I

— суммарный потребительский излишек,

PS = Ûπj(p) = ÛPSj(p)

j J j J

— суммарный излишек производителей.

226

227

Другими словами, индикатор благосостояния W(x, y), соответствующий любому равновесию, равен сумме излишков потребителей и производителей.

Заметим, что если p — равновесный вектор, предпочтения локально ненасыщаемы, то условия

pÛxi = pÛyj

i I j J

выполнены. Заметим также, что в этом случае состояние экономики Парето-оптимально, и поэтому W(x, y) достигает максимума на множестве допустимых состояний.

В сепарабельной экономике излишки потребителей и производителей представляют собой суммы соответствующих излишков на l рынках:

l l

CS = ÛCSk, PS = ÛPSk.

k=1 k=1

Представление суммарного спроса посредством модели репрезентативного потребителя

Очень часто при изучении моделей частного равновесия бывает удобно использовать предположение о том, что суммарный спрос порождается решением задачи одного потребителя. В том случае, когда такой потребитель существует, его называют репрезентатив-

ным потребителем.

Покажем, что в экономике EQ репрезентативный потребитель всегда существует.

Пусть xi(p) — вектор спроса i-го потребителя на первые l благ при ценах p. Тогда суммарный спрос всех потребителей равен

X(p) = Ûxi(p).

i I

В этих обозначениях репрезентативный потребитель будет порождать своими предпочтениями суммарный спрос X(p).

Покажем что репрезентативный потребитель в этих условиях существует, причем его предпочтения на множестве потребительских наборов (x, z), x > 0, могут быть представлены квазилинейной функцией полезности вида:

u(x, z) = v(x) + z.

Рассмотрим следующую задачу (задачу максимизации суммы полезностей от потребления 1-го блага при фиксированном количестве x- этого блага):

Ûvi(xi) →max x1,...xm i I

xi >0

Тогда в качестве v(x) мы можем взять значение этой задачи при x- = x. Покажем, что X(p) является решением задачи репрезентативного потребителя с функцией полезности, u(x, z) = v(x) + z, при любом векторе цен p> 0.

Предположим противное. Как мы видели, задачу представительного потребителя в случае квазилинейных предпочтений можно записать в эквивалентной форме:

227

228

v(x) – px→max x>0.

Пусть существует x~ >0, такой что

v(x~) – px~ > v(X(p)) – pX(p).

При этом, так как X(p) = Ûxi(p), и xi(p) допустимы в задаче ( ) при x- = X(p), то долж-

i I

но быть выполнено

v(x~) – px~ > Ûvi(xi(p)) – pÛxi(p).

i I i I

Заметим, что v(x~) = Ûvi(x~i), где (x~1, ..., x~m) — решение задачи ( ) при x- = x~. Таким обра-

i I

зом имеем

Ûvi(x~i) – pÛx~i >Ûvi(x~i) – px~ > Ûvi(xi(p)) – pÛxi(p).

Но это означает, что по крайней мере для одного из потребителей выполнено

vi(x~i) – px~i > vi(xi(p)) – pxi(p),

что противоречит оптимальности набора xi(p). Докажем, что

v(X(p)) = Ûvi(xi(p)),

i I

другими словами, индикатор благосостояния в экономике с одним представительным потребителем упорядочивает интересующие нас состояния экономики так же, как и индикатор благосостояния первоначальной экономики.

Предположим противное. Случай v(X(p)) < Ûvi(xi(p)) невозможен, т.к. xi(p) допустимы

i I

в задаче ( ) при x- = X(p). Поэтому предположим, что существует p такое, что

v(X(p)) > Ûvi(xi(p)).

i I

Пусть (x^1, ..., x^m) — решение задачи ( ) при x- = X(p). По определению v(X(p)) = Ûvi(x^

i I

i). Значит,

Ûvi(x^i) > Ûvi(xi(p)).

i I i I

С другой стороны,

Ûx^i <X(p) = Ûxi(p).

Умножим на p:

pÛx^i <pÛxi(p).

i I i I

Складывая два неравенства, получаем

228

229

Ûvi(x^i) – pÛx^i > Ûvi(xi(p)) – pÛxi(p).

Получили требуемое противоречие.

Задачи к главе

1.Докажите вторую часть Теоремы Ошибка! Источник ссылки не найден..

2.а) Постройте контрпример с вогнутыми функциями vi( ) и выпуклыми функциями cj( ), который бы показывал, что условие z^i > 0 i существенно в первой части Теоремы

Ошибка! Источник ссылки не найден..

б) Постройте контрпример, который бы показывал, что условие выпуклости функции издержек существенно в первой части Теоремы Ошибка! Источник ссылки не найден..

3.Докажите Теорему Ошибка! Источник ссылки не найден..

4.Покажите, что в случае квазилинейной экономики без ограничений на квазилинейное благо (EQ) Парето-граница в координатах полезностей ui представляет собой гиперпло-

скость вида Ûui = const.

i I

5.Докажите Теоремы Ошибка! Источник ссылки не найден., Ошибка! Источник ссылки не найден. и Ошибка! Источник ссылки не найден..

6.Докажите, что при xk(pk) > 0 выполнено

7. Пусть (x, y) — допустимое состояние квазилинейной экономики, и p > 0 — некоторый вектор цен, причем xi является решением задачи потребителя при ценах p, и

pÛxi = pÛyj

i I j J

Докажите, что

Ûui(xi, zi) = W(x, y) + Ûωi

i I i I

8. В экономике два блага (l + 1 = 2) и два потребителя, имеющие функции полезности u1 = x1 + z1 и u2 = 2 x2 + z2. Найдите функцию полезности репрезентативного потребителя.

9. Решите предыдущую задачу с функциями полезности u1 = –3/x31 + z1 и u2 = –3/x32 + z2.

229

230

10. Потребители (i = 1, ..., m) имеют квазилинейные функции полезности вида

Найдите функцию полезности репрезентативного потребителя в каждом из случаев.

11. Пусть предпочтения потребителей представляются квазилинейными сепарабельными функциями полезности. Тогда без потери общности можно считать, что в экономике два блага (l + 1 = 2). Пусть xi(p) — спрос на первое благо i-го потребителя при ценах p, D(p) = Ûxi(p) — суммарный спрос потребителей на первое благо, и p(x) = D–1(x) — обратная функция спроса. Предположим, что функция p(x) является непрерывной и убывающей при x > 0. Докажите, что если

x

v(x) = øp(q)dq,

0

то v(x) + z является функцией полезности репрезентативного потребителя.

12. В ситуации предыдущей задачи функция спроса на благо имеет вид

1 D(p) = 4p2.

Найдите функцию полезности репрезентативного потребителя.

230