
Бусыгин
.pdf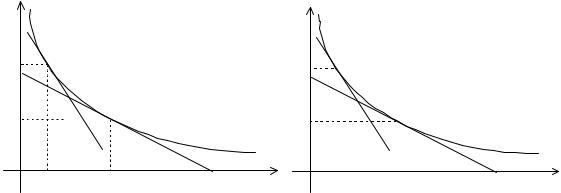
151 c(w1+dw1, w2+dw2, y) = c(w1, w2, y) или
|
dw1 |
|
∂c |
+dw2 |
∂c |
= 0 |
|
|
||||
|
|
|
|
|
|
|
||||||
|
|
|
∂w1 |
|
∂w2 |
|
|
|||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂c |
(w,y) |
|
|
* |
||||||
dw2 |
|
∂w |
|
w |
||||||||
1 |
|
|
|
r1( ,y) |
r1 |
|||||||
dw1 |
= – |
|
|
|
|
|
= – r2(w,y) = – |
|
|
|||
∂c |
(w,y) |
r2* |
||||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
∂w2 |
|
|
|
|
|
|||||
Аналогично получим соотношение для изокванты
|
|
∂f(r) |
|
|
dr2 |
|
∂r1 |
w1 |
|
dr1 |
= – |
|
|
= – w2. |
∂f(r) |
||||
|
|
∂r2 |
|
|
Эти соотношения двойственности показывают, что чем больше кривизна изокосты, тем меньше кривизна изокванты, и наоборот. Действительно, на графиках видно, что если две точки, r~ и r- одного графика далеки друг от друга, а их касательные близки (малая кривизна, то есть сильная взаимозаменяемость затрат в производстве), то в двойственном
графике соответствующие точки w-, w~ |
будут характеризоваться, наоборот, близким поло- |
||
жением, но сильно отличающимися касательными. |
|
|
|
x2 |
w2 |
|
|
x′ |
|
w′ |
|
x |
|
w |
|
|
Q(y) |
|
c(w,y)=const |
изокванта |
x1 |
изокоста |
w1 |
Рисунок 29 Связь между изокостами и изоквантами |
|
|
|
При полной взаимозаменяемости затрат любой структуре затрат соответствует одна и та же структура цен (см. рис ниже). Таким образом, структура цен не определяет однозначно структуру затрат.
151

152
x′2 |
|
|
w1 |
|
|
A |
w2 |
|
w2 |
c(w, y) |
|
|
|
||
x2 |
|
|
|
|
|
|
|
x′1 |
x1 |
w1 |
|
В любой точке отрезка |
Множество производных |
||
производная одна и та же |
одной точке |
||
Рисунок 30
A
x′1 x1
Кривая спроса
И наоборот, если затраты жестко взаимодополняемы, то цены, при которых эти затраты минимизирую издержки, определяются неоднозначно.
x2 |
|
w2 |
|
w1 |
|
||
|
|
w2 |
|
||||
x-2 |
|
w′2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
w″2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x-1 |
x1 |
w′1 |
w″1 w1 |
|
x-1 |
x1 |
|
Рисунок 31. Ситуация, обратная предыдущей
Еще один «нерегулярный» случай— невыпуклость IRS — иллюстрирует нижеследующий рисунок.
При разных векторах цен w один и тот же r.
x′2 |
|
|
w1 |
разрыв |
|
|
|
w2 |
|
x2 |
|
w2 |
|
|
|
|
|
|
|
x′1 |
x1 |
w1 |
|
x′1 x1 |
Рисунок 32. Изокванта не является выпуклой функцией
152

153
3. Классические (совершенные) рынки. Общее
равновесие
Анализ классических рынков уместно начать с перечисления характеристик рынков, при наличии которых их называют совершенными или классическими:
1)Отсутствие экстерналий — не опосредованных рынком влияний одних экономических субъектов на других. На поведение экономических субъектов поведение других экономических субъектов может влиять только через уровни цен и фиксированные денежные трансферты (например, получение потребителем прибыли с принадлежащих ему предприятий).
2)Существуют рынки всех благ, от которых зависят полезности потребителей и/или технологические множества производителей.
3)Существующие рынки является связанными: любое благо можно поменять на любое другое благо.
4)Совершенная конкуренция: каждый экономический субъект считает, что он не может повлиять на цены, принимает их как данные («достаточно мал»).
5)Нет издержек сделок, нет «рыночного трения». Цена покупки и цена продажи совпадают.
6)Совершенство информации. Уровни цен и характеристики обмениваемых благ известны каждому экономическому субъекту.
Реальные рынки далеки от совершенных рынков, однако их анализ выявляет некоторые эффекты, общие для всех рынков, и предваряет анализ несовершенных. В теоремах благосостояния мы покажем, что совершенный рынок как механизм согласования интересов экономических субъектов приводит к Парето-оптимальным исходам. В дальнейшем мы рассмотрим отдельные типы рыночных несовершенств и связанные с ними отклонения равновесий от Парето-оптимальности, то есть так называемые фиаско рынка.
Классическая модель экономики. Допустимые состояния
Пусть имеются l благ и m потребителей. Каждый из потребителей характеризуется неоклассическими предпочтениями {}i , }i , ~i} на множестве Xi, а также принадлежащими
ему ωi. Как правило в дальнейшем мы будем предполагать, что предпочтения потребителя представимы функцией полезности ui( )51. Множество Xi — это множество всех тех наборов, которые потребитель (физически) в состоянии потребить. Обычно в микроэкономических моделях множество Xi совпадает с неотрицательным ортантом: Xi = Êl+. Но мы не вводим такой априорной предпосылки, рассматривая и ситуации, когда Xi не совпадает с Êl+. Например, в ситуации, когда одним из благ является досуг, его потребление ограничено бюджетом времени потребителя. Другое ограничение может состоять в том, что потребление тех или иных благ не может быть ниже некоторой положительной пороговой величины («прожиточного минимума»). В ситуации, когда потребители сами создают некоторые блага, их можно моделировать отрицательными компонентами потребительских наборов.
Кроме того, пусть в экономике есть n производителей (фирм), каждый из которых характеризуется производственным множеством Yj (множеством векторов чистого выпуска); k-
51 Если неоклассические предпочтения непрерывны, то, в соответствии с теоремой Дебре, существует представляющая данные предпочтения непрерывная функция полезности ui( ).
153

154
я компонента вектора yj Yj показывает, сколько k-го блага выпускается j-м производителем. Технологические множества Yj в дальнейшем мы будем часто задавать в виде неявных производственных функций gj( ). Напомним, что по определению gj( ) называется неявной производственной функцией, если технология yj принадлежит технологическому множеству Yj тогда и только тогда, когда gj(yj) > 0. Как и ранее, с целью упрощения изложения мы будем рассматривать только скалярные неявные производственные функции. Переформулировка рассматриваемых ниже теорем для случая векторных неявных производственных функций (т.е. технологических множеств, задаваемых несколькими ограничениями) не связана с какими-либо концептуальными трудностями.
Таким образом, классическая модель экономики задается следующими компонентами: I = {1, ..., m} — множество потребителей,
J = {1, ..., n} — множество производителей (фирм), K = {1, ..., l} — множество товаров (благ),
Xi Êl — множество допустимых наборов i-го потребителя,
{}i , }i , ~i} — предпочтения потребителя или ui( ) — функция полезности i-го потреби-
теля (ui: Xi & Ê),
ωik — начальный (до обмена) запас k-го блага у i-го потребителя,
Yj Êl — технологическое множество (множество допустимых технологий) j-го производителя, gj( ) — неявная производственная функция (gj: Êl & Ê).
Для описания состояния экономики используются следующие переменные: xik — потребление i-м потребителем k-го блага (k K),
xi = (xi1, ..., xil) — потребительский набор i-го потребителя, x= (x1, ..., xm) — потребительские наборы всех потребителей,
yjk — производство j-м производителем k-го блага (это чистый выпуск, т.е. отрицательные компоненты соответствуют затратам),
yj = (yj1, ..., yjl) — технология j-го производителя,
y= (y1, ..., yn) — набор технологий всех производителей.
Набор (x, y) = ({xi}i I, {yj}j J) называют состоянием экономики. Естественно рассматривать не все такие наборы, а только (физически) допустимые состояния экономики.
Определение 1.
Под допустимым состоянием экономики принято понимать такую пару (x, y), что
при всех i I вектор xi является допустимым набором для i-го потребителя (т.е.
xi Xi),
при всех j J вектор yj является допустимой технологией для j-го производителя (т.е.
yj Yj),
для экономики в целом выполнены балансы (общий объем потребления в экономике по каждому благу равен сумме общего объема производства и суммарных начальных запасов):
Ûxik = Ûωik + Ûyjk , k K.
i I i I j J
154

155
Отметим, что часто в моделях общего равновесия используются полубалансы:
Ûxik <Ûωik + Ûyjk , k K.
i I i I j J
При этом строгое неравенство должно означать, что в экономике осталось непотребленное благо. В рамках моделей с балансами в виде равенств возможность «выбрасывать» блага можно моделировать с помощью технологических множеств со свободой расходования по данным благам. В определенном смысле используемый здесь подход является более общим, поскольку позволяет моделировать блага, утилизация которых требует затрат ресурсов.
Любой механизм координации решений экономических субъектов должен приводить к допустимому состоянию экономики. Анализ экономического механизма включает описание условий, при которых он «работоспособен», и свойств тех допустимых состояний, к которым он может привести. Ниже мы проведем такое исследование для механизма ценовой координации совершенных рынков.
Общее равновесие (равновесие по Вальрасу)52
В этом параграфе мы вводим понятие равновесия и обсуждаем ту роль, которую играет это понятие в неоклассическом анализе.
Субъекты экономики в моделях общего равновесия
МОДЕЛЬ ПОТРЕБИТЕЛЯ
Ниже через pk будем обозначать цену k-го блага, а через p вектор всех цен (p1, ..., pl). Пусть потребитель i I, предпочтения }i которого зависят только от собственного потребления xi = {xik}k K, сталкивается с рыночными ценами p приобретаемых им благ. Как и ранее, мы предполагаем, что потребитель выбирает наилучший потребительский набор из тех, которые ему доступны, т.е. потребительских наборов, принадлежащих бюджетному множеству. Под бюджетным множеством подразумевается множество допустимых потребительских наборов, xi Xi, удовлетворяющих бюджетному ограничению:
pxi = Ûpkxik <βi, k K
т.е. бюджетное множество имеет вид
Bi(p, βi) = {xi Xi | pxi <βi}
Здесь βi = βi( ), где βi( ) — функция, задающая доход потребителя. Способ формирования дохода зависит от конкретного варианта экономики. Например, в экономике обмена доход потребителя формируется за счет продажи по рыночным ценам его начальных запасов:
βi(p, ωi) = pωi = Ûpkωik. k K
В модели классических рынков предполагается, что начальные запасы ωi, цены, а также доходы из других источников не зависят от выбора потребителя (определяются экзогенно). Другими словами, потребитель считает, что не влияет на цены и свою исходную (до
52 Развитие этой модели связано с такими именами как Адам Смит (1776), Давид Рикардо (1817), Леон Вальрас (1874,1883), Кеннет Эрроу и Жерар Дебрё (1950-е гг.).
155

156
торговли) собственность, принимая их как данные. Поэтому при описании выбора потребителя при заданных ценах будем считать, что доходы фиксированы.
Таким образом, набор x-i является выбором потребителя, сталкивающегося с ценами p и имеющего доход βi, если
1)набор x-i принадлежит бюджетному множеству, x-i Bi(p, βi);
2)любой потребительский набор xi Xi лучший, чем x-i, не принадлежит бюджетному множеству, т.е. xi }i x-i xi Bi(p, βi).
Если предпочтения потребителя описываются функцией полезности ui( ), то его выбор моделируется как решение задачи максимизации функции полезности по xi Xi при бюджетном ограничении. Таким образом, задача потребителя имеет вид
ui(xi) →max xi
xi Bi(p, βi).
При дифференцируемости функций полезности можно охарактеризовать решение задачи потребителя, т.е. оптимальный для данного потребителя набор x-i, при помощи теоремы Куна—Таккера в дифференциальной форме (см. Приложение).
Будем считать, что решение задачи потребителя внутреннее, т.е.53 x-i int(Xi).
Это позволяет не учитывать ограничение xi Xi. Функция Лагранжа для задачи потребителя равна
L = ui(xi) + νi(βi – Ûpkxik),
k K
где νi — множитель Лагранжа для бюджетного ограничения.
По теореме Куна—Таккера (при выполнении условий регулярности, которые в данном случае эквивалентны тому, что не все цены равны нулю) существует множитель Лагранжа νi > 0, такой что в оптимуме
|
∂L(x |
, ν ) |
|
|||||
|
|
|
-i |
|
|
i |
= 0, |
k K, |
|
|
∂xik |
||||||
|
|
|
|
|||||
или |
|
|
|
|
|
|
||
|
|
∂u |
(x |
) |
|
|
|
|
|
|
i |
-i |
|
= ν p , k K. |
|||
|
|
|
|
|
||||
|
|
∂xik |
|
|
|
i k |
|
|
|
|
|
|
|
|
|
||
Другими словами, |
|
|
|
|
|
|
||
ui(x-i) = νip,
то есть градиент функции полезности коллинеарен вектору цен. Если предположить, что в решении задачи потребителя x-i не все производные функции полезности равны нулю,
ui(x-i) ≠0, то νi > 0. Такое решение задачи потребителя может иметь место только если цены, с которыми он сталкивается, не все равны нулю. Исключая множитель Лагранжа, для любых двух благ k, s K, таких что pk ≠0, получаем, что
53 Напомним, что это означает, что x-i принадлежит Xi вместе с некоторой своей окрестностью.
156

157
ps = ∂ui(x-i)/∂xis. pk ∂ui(x-i)/∂xik
Следовательно, решение задачи потребителя характеризуется равенством предельной нормы замещения любых двух благ отношению цен этих благ. Таким образом, мы получили классическую дифференциальную характеристику решения задачи потребителя.
Это одно из условий первого порядка, т.е. необходимое условие максимума. Поскольку, как мы предположили, градиент не равен нулю, то νi > 0, и по условию дополняющей нежесткости теоремы Куна—Таккера получаем, что бюджетное ограничение выходит на равенство:
pxi = βi.
Это еще одно условие первого порядка.
Условия первого порядка задают систему уравнений, любое (внутреннее) решение которой по обратной теореме Куна—Таккера является решением задачи потребителя, если выполнено дополнительное условие, состоящее в том, что множество Xi выпукло, а функция полезности ui( ) вогнута.
Напомним, что ui( ) называется вогнутой, если
ui(αx+ (1 – α)y) >αui(x) + (1 – α)ui(y)
для любого α [0,1] и любых x и y.
Замечание: На самом деле достаточно, чтобы данная функция полезности могла быть преобразована в вогнутую каким-либо монотонным (строго возрастающим) преобразованием. Монотонное преобразование функции полезности не меняет предпочтений потребителя. Так, например, функция u(x, y) = xy и ее логарифм ln(u(x, y)) = ln(x) + ln(y) задают одни и те же потребительские предпочтения, хотя первая не вогнута, а вторая вогнута и допускает поэтому применение теоремы Куна—Таккера. Следовательно, допускает его и первая, приводимая к вогнутой.
Существуют и более слабые наборы условий, гарантирующие тот факт, что условие первого порядка приводят к решению задачи потребителя. Обычно они включают выпуклость предпочтений (или квазивогнутость представляющих их функций полезности) (см. задачу???). Мы приводим здесь более сильные, чем это необходимо, достаточные условия оптимальности, чтобы использовать в анализе хорошо известный читателям аппарат теории экстремальных задач — эффективное средство их анализа.
Отдельного рассмотрения требует случай, когда решение задачи потребителя не является внутренним. Пусть, например, Xi = Êl+ и потребление некоторых благ в решении задачи потребителя может быть равно нулю. Для получения дифференциальной характеристики такого решения опять можно воспользоваться теоремой Куна—Таккера. Получаем, что оптимальный набор должен удовлетворять условиям
|
|
∂L(x |
) |
|
∂L(x |
) |
|
|
||||
|
|
|
-i |
|
<0, причем |
|
-i |
|
= |
|||
|
|
|
|
|
|
|
∂x |
|
||||
|
|
∂x |
|
|
|
|
|
|
|
|
||
|
|
|
ik |
|
|
|
ik |
|
|
|
||
или |
-i |
|
|
|
|
|
i -i |
|
||||
|
|
i |
) |
|
|
|
|
) |
||||
|
∂u |
(x |
|
<νipk, причем |
∂u (x |
|||||||
|
|
∂x |
|
|
∂x |
|
|
|
||||
|
|
|
ik |
|
|
|
|
|
ik |
|
||
0, если x-ik > 0, k K.
=νipk, если x-ik > 0, k K.
157

158
МОДЕЛЬ ПРОИЗВОДИТЕЛЯ
При выборе объемов производства yj = {yjk}k K каждая фирма j J ограничена своим технологическим множеством Yj.
В качестве целевой функции «классического» производителя берется его прибыль
πj = pyj = Ûpkyjk. k K
В ситуации совершенной конкуренции производитель, как и потребитель, предполагает, что не может влиять на цены. Таким образом, задачей производителя является максимизации прибыли при технологических ограничениях:
pyj →max yj
yj Yj.
Если технологическое множество задано неявной производственной функцией gj( ), то задача производителя записывается как
pyj →max yj
gj(yj) >0.
При дифференцируемости функции gj( ) решение этой задачи также можно охарактеризовать при помощи теоремы Куна—Таккера в дифференциальной форме. Функция Лагранжа для задачи производителя равна
L = Ûpkyjk + κj gj(yj),
k K
где κj — множитель Лагранжа, соответствующий технологическому ограничению.
По теореме Куна—Таккера (при выполнении условий регулярности, которые в данном случае эквивалентны тому, gj(yj) ≠0) существует множитель Лагранжа κj >0, такой что в оптимуме
∂L(y- , κ )
∂ j j = 0, k K,
yjk
или
κj∂gj(y-j) = pk, k K.
Другими словами,
κj gj(y-j) = p,
то есть градиент неявной производственной функции коллинеарен вектору цен. Если не все цены равны нулю (p≠0), то κj > 0. Исключая множитель Лагранжа κj, для любых двух благ k, s K, таких что pk ≠0, получаем, что
ps = ∂gj(y-j)/∂yjs. pk ∂gj(y-j)/∂yjk
Следовательно, решение задачи производителя характеризуется равенством предельной нормы трансформации любых двух благ отношению цен этих благ. Таким образом, мы получили классическую дифференциальную характеристику решения задачи производителя.
158
159
Условия первого порядка задают систему уравнений, любое решение которой по обратной теореме Куна—Таккера является решением задачи потребителя, если выполнено дополнительное условие, что функция gj( ) вогнута.
Модели общего равновесия
Теперь модели отдельных экономических субъектов, потребителей и производителей, объединим в модели рынка (экономики) в целом. Такие модели называются моделями об-
щего равновесия .
МОДЕЛЬ ОБМЕНА
В случае, если экономика не содержит производства, то она называется экономикой обмена. Таким образом, экономика обмена характеризуется множеством потребителей, множествами допустимых потребительских наборов потребителей, их предпочтениями и начальными запасами, т.е.
EE = {I, (Xi, }i, ωi)i I}.
В экономике обмена потребитель получает доход только от начальных запасов. Введем теперь определение равновесия для экономики обмена.
Определение 2.
Равновесием по Вальрасу в экономике обмена EE называется набор (p-, x-), такой, что:
каждый вектор x-i является решением задачи потребителя i при ценах p- и доходе βi = p-
ωi;
x- — допустимое состояние экономики EE, следовательно, для всякого блага k выпол-
нено |
|
Ûx-ik = Ûωik. |
|
i I |
i I |
x21 |
|
x12 |
|
ω |
|
L1++(x ) |
|
-1 |
|
x- |
|
L2++(x ) |
|
-2 |
|
x11 |
|
x22 |
|
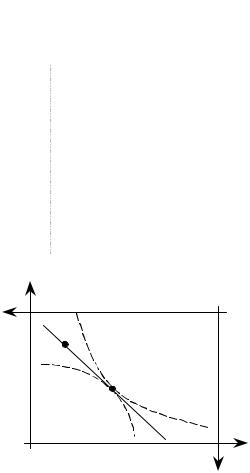
Рисунок 33. Иллюстрация равновесия на ящике Эджворта |
|
Удобным инструментом для иллюстрации экономики обмена является диаграмма Эджворта (ящик Эджворта). Эта диаграмма позволяет наглядно представить экономику с 2 потребителями и 2 благами. Обычно предполагается, что множества допустимых потребительских наборов в такой экономике имеют вид x1 >0 и x2 >0. На диаграмме Эджворта потребление 1-го потребителя (x11, x12) представляется в обычной системе координат, а
потребление 2-го потребителя (x21, x22) — в перевернутой с центром в точке (ωΣ1, ωΣ2), если смотреть из системы координат 1-го участника. Точка (x11, x12) в первой системе коор-
159

160
динат совпадет с точкой (x21, x22) во второй системе координат, что позволяет изобразить состояние x одной точкой на данной диаграмме.
Рис. 33 иллюстрирует на ящике Эджворта концепцию равновесия. Общая бюджетная прямая в равновесии проходит через точку начальных запасов ω и равновесный вектор x-. Наклон бюджетной прямой соответствует отношению равновесных цен p-1/p-2. У каждого потребителя множество L++i (x-i) наборов, которые лучше, чем равновесный набор x-i, лежит по соответствующую сторону от бюджетной прямой, так что это множество не имеет общих точек с бюджетным треугольником данного потребителя.
МОДЕЛЬ ЭРРОУ—ДЕБРЕ
Модель Эрроу—Дебре является развитием модели обмена и включает в себя, помимо потребителей, производственный сектор.
Особенностью модели является и то, что в ней специфицированы права собственности потребителей на владение фирмами, производящими продукцию. Таким образом, в модели предполагается, что все предприятия кому-то принадлежат, то есть каждый потреби-
тель i владеет долей γij предприятия j, причем Ûi Iγij = 1, γij >0.
Наличие производственного сектора влияет и на постановку задачи потребителя, поскольку доход потребителя складывается из того, что он может выручить от продажи начальных запасов и из его дохода от участия в прибыли. Поэтому доход потребителя при ценах p и величинах прибыли πj равен
βi = Ûpkωik + Ûγijπj. k K j J
В целом экономика Эрроу—Дебре характеризуется множеством потребителей, множествами допустимых потребительских наборов потребителей, их предпочтениями и начальными запасами, множеством производителей, их производственными множествами и долями потребителей в прибыли фирм, т.е.
EAD = {I, (Xi, }i, ωi)i I, J, (Yj)j J, (γij)i I, j J}.
Определение 3.
Равновесием по Вальрасу в экономике Эрроу—Дебре EAD называется набор (p-, x-, y-), та-
кой что:
каждый вектор x-i является решением задачи потребителя i при ценах p- и доходе βi = p-
ωi + Ûγijp-y-j ; j J
каждый вектор y-j является решением задачи производителя j при ценах p-;
(x-, y-) — допустимое состояние экономики EAD, следовательно, для всякого блага k выполнено
Ûx-ik = Ûωik + Ûy-jk.
i I |
i I |
j J |
160
