Бусыгин

191

Ûx~i = Ûωi + Ûy~j.

i I i I j J

Получено противоречие, поэтому для (x-, y-) нельзя найти Парето-улучшение. Это означает, что (x-, y-) — Парето-оптимум.

*

Рассмотрим пример экономики с потребителями, характеризующимися локальным насыщением, и проиллюстрируем его с помощью ящика Эджворта.

Пример 2.

Первый потребитель имеет функцию полезности с «толстой» кривой безразличия

У второго же потребителя функция полезности линейна

u2 = x21 + x22.

Начальные запасы в экономике достаточно большие.

Рисунок 39. Контрпример к первой теореме благосостояния

Данная ситуация представляет собой контрпример к первой теореме благосостояния и показывает важность условия локальной ненасыщаемости. Точки в заштрихованной области Рис. 39 принадлежат слабой границе Парето, но не сильной. Их можно реализовать как равновесие при ценах p1 = p2 = 1, но они не являются Парето-оптимальными.

Перейдем к доказательству того, что всякое Парето-оптимальное состояние можно реализовать как равновесие (вторая теорема благосостояния). Мы докажем здесь эту теорему в предположении дифференцируемости функций с использованием теоремы Куна— Таккера.

Теорема 14 (вторая теорема благосостояния)

Пусть (x^, y^) — Парето-оптимальное состояние экономики, причем

#функции полезности и производственные функции дифференцируемы,

#множества Xi выпуклы, а функции полезности и производственные функции вогнуты61,

61 Здесь достаточно потребовать «приводимость к вогнутости».

191

192

#для всех потребителей x^i int(Xi) (т.е. рассматриваемый Парето-оптимум внутренний),

#в рассматриваемом состоянии градиенты всех функций полезности и производственных функций не равны нулю:

ui(x^i) ≠0, i I,

gj(y^j) ≠0, j J.

Тогда найдется вектор цен p и трансферты Si, i = 1, ..., m, такие что (p, x^, y^) — общее равновесие.

Доказательство.

Выше мы доказали, что в условиях теоремы найдутся множители Лагранжа λi > 0 (i I),

Возьмем в качестве равновесных цен множители Лагранжа для балансовых ограничений, т.е. pk = σk , k K и выберем такие трансферты Si, чтобы доход каждого потребителя совпадал с расходами, требуемыми на покупку набора x^i при ценах p (βi = px^i), т.е.

Si = βi – pωi – Ûγijpy^j = p(x^i – ωi – Ûγijy^j).

Несложно проверить, что сумма этих трансфертов равна нулю.

Для того, чтобы доказать, что (p, x^, y^) является равновесием, нам достаточно доказать, (i) что для всех потребителей x^i является решением задачи потребителя при ценах p и доходах px^i, и (ii) что для всех производителей y^j является решением задачи производителя при ценах p.

(i) Очевидно, что набор x^i является допустимым в задаче потребителя. Докажем, что он является оптимальным. Для этого воспользуемся обратной теоремой Куна—Таккера.

Требуется найти неотрицательный множитель Лагранжа νi для бюджетного ограничения, такой что выполнено условие первого порядка (выведенное ранее)

∂ui(x^i)

∂xik = νipk, k K.

Этому требованию удовлетворяет νi = 1/λi, поскольку выполнено λi ∂ui(x^i)/∂xik = σk и

λi > 0.

Условие дополняющей нежесткости для бюджетного ограничения выполнено, поскольку в точке x^i бюджетное ограничение активно. Поскольку функция полезности вогнута, а множество Xi выпукло, то выполнены все требования обратной теоремы Куна—Таккера. Т.е. x^i — решение задачи потребителя.

(ii) Докажем теперь, что технология y^j является оптимальной для j-го производителя. Требуется найти неотрицательный множитель Лагранжа κj для технологического ограничения, такой что выполнено условие первого порядка

192

193

∂gj(y^j)

κj ∂yjk = pk, k K.

Этому требованию удовлетворяет κj = µj. Условие дополняющей нежесткости для технологического ограничения выполнено, поскольку соответствующее условие с точностью до замены µj на κj выполнено в Парето-оптимуме. Таким образом, выполнены условия Ку- на—Таккера, и поскольку производственная функция вогнута, то y^j — решение задачи производителя.

*

Замечание.

В экономике без трансфертов, чтобы доходы βi равнялись требуемым расходам px^i, следует соответствующим образом распределить собственность, то есть указать начальные запасы ωi и доли в прибылях γij. Для этого достаточно найти долю θi каждого потребителя в совокупных расходах потребителей,

θ = Ûpx^i ,

i spx^s

и поделить собственность в соответствующих пропорциях, т.е. взять γij = θi i, j и ωi = θiωΣ i, где ωΣ — совокупные начальные запасы.

В экономике чистого обмена достаточно выбрать ωi = x^i.

Использование теоремы Куна—Таккера в дифференциальной форме — только один из возможных путей доказательства. Мы воспользовались им здесь, поскольку этот подход понадобится нам в дальнейшем для проверки противоположных утверждений — о неоптимальности несовершенных рынков. Условие дифференцируемости функций во второй теореме благосостояния на самом деле избыточны.

Теорема 15 (вторая теорема благосостояния без дифференцируемости)

Пусть

#множества допустимых потребительских наборов Xi выпуклы, предпочтения потребителей }i выпуклы, непрерывны и локально ненасыщаемы,

#технологические множества Yi каждого производителя выпуклы.

Тогда если (x^, y^) — оптимальное по Парето состояние и x^i int(Xi) i (т.е. данное Па- рето-оптимальное состояние является внутренним), то существуют цены p и трансферты Si, i = 1, ..., m, такие что (p, x^, y^) является общим равновесием.

Доказательство.

Введем ряд обозначений которые нам понадобятся в дальнейшем для доказательства этого утверждения.

Обозначим множество наборов лучших для потребителя i, чем x^i, через

L++i (x^i) = {xi Xi | xi }i x^i}.

Поскольку предпочтения потребителей выпуклы, и множества допустимых потребительских наборов Xi выпуклы, то, как несложно показать, L++i (x^i) также выпуклы и, значит, их сумма

L++(x^) = ÛiL++i (x^i) = {Ûi xi | xi Xi, xi }i x^i}

193

194

выпукла. Кроме того, L++i (x^i) непусты по локальной ненасыщаемости, значит и L++(x^) непусто.

Множество производственных возможностей,

YΣ + ωΣ = Ûj Yj + ωΣ = {Ûj yj + ωΣ | yj Yj},

тоже является выпуклым в силу выпуклости технологических множеств и непустым, так как ему принадлежит точка Ûjy^j + ωΣ.

Поскольку (x^, y^) — оптимум Парето, то множества L++(x^) и YΣ + ωΣ не имеют общих точек:

L++(x^) ](YΣ + ωΣ) = .

Предположим, что существует общая точка z L++(x^) и z YΣ + ωΣ. Это означало бы, что существует состояние экономики (x, y), такое что xi Xi, xi }i x^i i, yj Yj j, Ûi xi = z и Ûj yj + ωΣ = z. Тем самым мы нашли бы допустимое состояние экономики, которое доминирует62 оптимальное по Парето состояние (x^, y^), чего быть не может.

Поскольку множества L++(x^) и YΣ + ωΣ выпуклы, непусты и не пересекаются, к ним применима теорема об отделимости. Поэтому существует вектор p Êl, p≠0 и число r Ê, такие что

pz>r, если z L++(x^)

и

pz<r, если z YΣ + ωΣ.

Пусть x ={xi} — такой набор допустимых потребительских наборов, что xi }i x^i i, что

можно по аналогии записать как x L+(x^). Покажем, что pÛixi >r. Из локальной ненасыщаемости предпочтений }i следует, что для любого натурального числа N в окрестности V1/N(xi) набора xi существует набор xNi , такой, что xNi }i xi, где V1/N(xi) — шар с цен-

тром xi и радиусом 1/N. Поскольку xNi }i xi }i x^i, то ÛixNi L++(x^), откуда pÛixNi >r. Заметим, что последовательность xNi сходится к xi. Переходя к пределу по N, получим требуемое неравенство.

Введем обозначение

z^ = Ûix^i = Ûjy^j + ωΣ.

(Второе равенство здесь является следствием балансов по благам).

Поскольку z^ L+(x^) (по рефлексивности отношения }i — каждый из наборов x^i не хуже себя самого), то pz^ >r. С другой стороны, так как Парето-оптимум технологически допустим, то z^ YΣ + ωΣ, и pz^ <r. Следовательно, r = pz^.

Таким образом, мы нашли гиперплоскость, проходящую через z^ и разделяющую множества YΣ + ωΣ и L+(x^) (см. Рис. 40). Возьмем коэффициенты этой гиперплоскости p в качестве цен и покажем, что (p, x^, y^) является равновесием при соответствующем подборе трансфертов.

62 Причем строго доминирует.

194

p(yj + Ûs≠jy^s + ωΣ) <pz^ = p(Ûsy^s + ωΣ).

Отсюда pyj <py^j. Другими словами, производитель не может при ценах p увеличить свою прибыль, выбрав yj вместо y^j, то есть y^j — решение задачи производителя.

Аналогичным образом доказывается, что любой набор xi Xi, который не хуже x^i (xi }i x^ i), не может стоить дешевле, чем x^i в ценах p. Действительно, так как (x^1, ..., xi, ..., x^n) не хуже для каждого потребителя, чем x^, то

p(xi + Ûs≠ix^s) >pz^ = pÛsx^s.

Таким образом, из xi }i x^i следует pxi >px^i.

Докажем, что при ценах p и доходе βi = px^i полезность каждого потребителя i максимальна в точке x^i. Для этого требуется усилить доказанный только что факт и доказать, что из xi }i x^i следует pxi > px^i. Другими словами, требуется доказать, что лучший набор xi (xi Xi и xi }i x^i) должен стоить дороже, чем x^i в ценах p. Мы уже доказали, что pxi >px^i, поэтому осталось показать, что равенство здесь достигаться не может.

Предположим, что это не так и pxi = px^i.

Условие x^i int(Xi) означает, что x^i принадлежит множеству Xi вместе с некоторой своей окрестностью. Поскольку не все цены равны нулю (p≠0), то в этой окрестности найдется набор x′i, который в ценах p стоит дешевле x^i и, следовательно, дешевле xi. Действительно, пусть pk ≠0 для некоторого блага k. Если pk > 0, то можно немного уменьшить потребление этого блага по сравнению с x^ik, а если pk < 0, то немного увеличить. Таким образом, существует допустимый набор x′i, такой что px′i < pxi.

Рассмотрим выпуклые комбинации αx′i + (1 – α)xi, α [0, 1]. Поскольку множество допустимых потребительских наборов Xi выпукло, то все такие наборы допустимы. По непрерывности предпочтений найдется достаточно малое положительное α, такое что набор

x″i = αx′i + (1 – α)xi.

лучше, чем x^i. Кроме того, поскольку px′i < px^i = pxi, то px″i < pxi.

Но, с другой стороны, из x″i }i x^i следует, что px″i >px^i. Получили противоречие.

195

196

Таким образом, pxi > px^i. Значит, невозможно найти допустимый набор, который был бы лучше x^i, но стоил бы не дороже, чем x^i. Таким образом, x^i — решение задачи потребителя при ценах p и доходе βi = px^i.

Рисунок 41. Иллюстрация к доказательству второй теоремы благосостояния

Для того, чтобы доказать, что (p, x^, y^) — равновесие Вальраса, нам осталось найти такие трансферты, равные в сумме нулю, чтобы с учетом трансфертов βi = px^i. Рассуждения здесь повторяют рассуждения предыдущей теоремы.

*

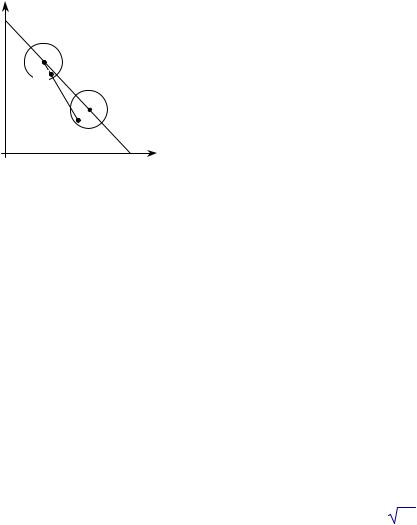
Рассмотрим примеры того, что отказ от предположений второй теоремы благосостояния приводит к тому, что она перестает быть верной. При этом удобно воспользоваться для иллюстрации ящиком Эджворта. Для того, чтобы на основе Парето-оптимума можно было построить равновесие, требуется найти прямую, которая бы разделяла множества L++1 (x^1) и L++2 (x^2) на диаграмме Эджворта. Например, на Рис. 33 такая гиперплоскость имеется, поэтому точка x- является одновременно Парето-оптимальной и равновесной. На Рис. 36 первый потребитель имеет невыпуклые предпочтения и Парето-оптимальную точку x^ нельзя реализовать как равновесие — не существует прямой, которая бы разделяла L++1 (x^1) и L++2 (x^2). Приведем еще несколько примеров.

Пример 3.

Пусть потребители имеют функции полезности u1 = x11 + x12 и u2 = x22.

Правый нижний угол ящика Эджворта (x^) представляет собой оптимум Парето, но не может быть реализован как равновесие ни при каких ценах (см. Рис. 42). Эта экономика представляет собой контрпример ко второй теореме благосостояния с не внутренним оптимумом Парето. Прямая, разделяющая L++1 (x^1) и L++2 (x^2), существует — она проходит горизонтально. Однако это разделение нестрогое, поскольку частично эта прямая лежит в L++1 (x^1). Действительно, несложно проверить, что при ценах p1 = 0 и p2 > 0 набор x^1 не является решением задачи первого потребителя, так как полезность не ограничена сверху.

В следующем примере вместо ящика Эджворта используется диаграмма, аналогичная той, что изображена на Рис. 34.

Пример 4.

Пусть экономика состоит из одного потребителя с локально насыщаемыми предпочтениями и одного производителя (см. Рис. 43). Точка Парето-оптимума x^ = ω+ y^ лежит на границе производственных возможностей и находится внутри «толстой» кривой безразличия. Поскольку множество производственных возможностей и множество лучших наборов L++(x^) не имеют на диаграмме общих точек, то это действительно оптимум.

196

197

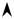x12

x21

L++1 (x^1)

x^ x11

L++2 (x^2)

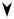x22

Рисунок 42. Контрпример ко второй теореме благосостояния: не внутренний Парето-оптимумом

Чтобы точка x^ = ω+ y^ была равновесной, нужно, чтобы отношение цен было равно наклону границы производственных возможностей в этой точке. Однако в условиях бюджетного ограничения, соответствующего такому наклону бюджетной прямой, точка x^ не будет решением задачи потребителя, так как гипотетический бюджетный треугольник имеет общие точки с множеством L++(x^).

Аналогичный пример можно построить, если взять Парето-оптимум внутри множества производственных возможностей и внутри «толстой» кривой безразличия. Из такого оптимума нельзя сконструировать равновесие, поскольку (при ненулевых ценах) решение задачи производителя должно лежать на границе технологического множества. На этом примере видно, что рыночное равновесие, в отличие от концепции оптимальности по Парето, предполагает самостоятельную роль предприятий и технологическую эффективность. В равновесии достигается технологическая эффективность даже тогда, когда с общественной точки зрения она бесполезна.

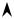x2 = ω2 + y2

Рисунок 43. Контрпример ко второй теореме благосостояния: предпочтения потребителя не являются локально ненасыщаемыми

Оба эти примера демонстрируют некоторую содержательную недостаточность второй теоремы благосостояния. Дело в том, что в обеих экономиках имеются Парето-оптимумы, эквивалентные рассматриваемым Парето-оптимумам с точки зрения потребителей (в данном случае — единственного потребителя), на основе которых уже можно сконструировать равновесие.

Задачи

32. Привести пример равновесия в экономике обмена с двумя потребителями и двумя благами, в котором первая теорема благосостояния была бы не применима из-за нарушения предположений, и равновесие нарушало бы ее утверждение. Можно привести графиче-

197

198

ский пример, либо указать конкретные начальные запасы, ω1, ω2, функции полезности u1( ), u2( ) и равновесие (p, x).

33.Привести пример равновесия в экономике обмена с двумя потребителями и двумя благами, в котором первая теорема благосостояния была бы не применима из-за нарушения предположений, но утверждение первой теоремы благосостояния оставалось бы справедливым.

34.Привести пример экономики обмена с двумя потребителями и двумя благами, графический или с конкретными начальными запасами ω, функциями полезности u1( ), u2( ), и

состоянием этой экономикиx, для которой вторая теорема благосостояния не применима

и

(А) утверждение второй теоремы благосостояния остается справедливым. (В) утверждение второй теоремы благосостояния неверно.

35.Сформулируйте предположения первой теоремы благосостояния для экономики обме-

на.

36.Сформулируйте предположения второй теоремы благосостояния для экономики обме-

на.

37.Сформулируйте и докажите теоремы благосостояния в модели обмена в условиях строгой монотонности, строгой выпуклости предпочтений и положительности совокупных начальных запасов.

38.Для каждого из предположений второй теоремы благосостояния покажите (приведя соответствующий пример), что отказ от этого предположения приводит к тому, что утверждение теоремы оказывается неверным.

39.Что можно сказать о соотношениях предельных норм замены товаров в потреблении и производстве в точке равновесия? Связано ли это соотношение с отсутствием Паретоулучшающего изменения состояния? Если данное соотношение нарушается, как следует строить Парето-улучшение данного состояния экономики?

40.Пусть допустимые потребительские наборы задаются неравенствами xi >0. Какие из функций полезности представляют предпочтения, удовлетворяющие условиям первой и (или) второй теоремы благосостояния?

1)u(x1, x2) = x1,

2)u(x1, x2) = –x1,

3)u(x1, x2) = const,

4)u(x1, x2) = x21 + x22,

5)u(x1, x2) = x1 + x2 ,

198

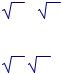
199

6)u(x1, x2) = min{x1, x2},

7)u(x1, x2) = exp(x1)x2,

8)u(x1, x2) = x1x2,

9)u(x1, x2) = x1 – 3x2,

10)u(x1, x2) = x1 + 2x2.

41.Пусть начальные запасы в экономике обмена лежат на Парето-границе. Какие дополнительные условия гарантируют, что на основе точки начальных запасов можно построить равновесие?

42.Пусть в экономике обмена с двумя потребителями их функции полезности равны

u1(x1) = x211 + x212,

и

u2(x2) = x221 + x222.

Найти Парето-границу. Какие из точек Парето-границы можно реализовать как равновесие подбором цен и распределения собственности? Решите эту задачу в случае, когда

(1)суммарные начальные запасы двух благ одинаковы,

(2)суммарные начальные запасы двух благ различаются.

43. В классической экономике обмена с двумя потребителями, функции полезности последних, заданные на Ê2+, равны

(а) u1 = x1 – x2, u2 = 6 + x1 – x2,

(b) u1 = min{x1, x2}, u2 = 6 – x1 + x2,

(c) u1 = x1 x2, u2 = 6 – x1 – x2.

В каких из трех экономик окажется, что...

1)любое равновесие Парето-оптимально (почему именно в этих, а в других — нет?),

2)любое Парето-оптимальное состояние x> 0 можно превратить в равновесие подбором распределения собственности (почему именно в этих, а в других — нет?).

44.Сформулируйте и докажите вариант первой теоремы благосостояния (о Паретооптимальности равновесий) на основе сопоставления дифференциальных характеристик Парето-оптимальных и равновесных состояний. Какие дополнительные предположения о свойствах функций полезности (помимо дифференцируемости) необходимо сделать?

45.Первая теорема благосостояния (о Парето-оптимальности равновесий) доказывается от противного: предполагаем, что существует альтернативное к равновесному состояние (x, y), более желательный для некоторого потребителя i. Условие локальной ненасыщаемости (сформулировать) используется для того, чтобы проверить, что:

А) альтернативный вариант дороже чем равновесный для потребителя i; Б) спрос сбалансирован с предложением в равновесии;

199

200

В) ……………….

Укажите словами верный вариант взамен приведенных и запишите его формулой.

46.В доказательстве второй теоремы благосостояния (о реализуемости Парето-оптимума), не использующем дифференцируемость, условие выпуклости используется для того, что-

бы применить теорему ……... ...... .... .….. к множествам .... .... .... ...... ......... ......... .........

......... ....… ………. Сформулируйте применяемую теорему и определение соответствующих множеств.

47.В доказательстве второй теоремы благосостояния (о реализуемости Парето-оптимума), использующем дифференцируемость, условие выпуклости используется для того чтобы с помощью теоремы …. .... .... ….. ..... доказать, что соответствующие компоненты построенного состояния экономики являются решениями задач .…… … … …… … …… … . Сформулируйте применяемую теорему, соответствующие задачи и способ применения теоремы.

48.При доказательстве второй теоремы благосостояния (о реализуемости Паретооптимума как равновесия), использующем дифференцируемость, условия на градиенты функций нужны для того, чтобы применить Теорему ……….. к задаче ………………

49.При доказательстве второй теоремы благосостояния (о реализуемости Паретооптимума как равновесия) при отсутствии свойства локальной ненасыщаемости не удает-

ся показать, что .................................... , так как может оказаться что.....................................

(сформулируйте ответ в трех-пяти фразах и поясните, сказанное рисунком).

50. При доказательстве второй теоремы благосостояния (о реализуемости Паретооптимума как равновесия) при невыполнении условия выпуклости предпочтений не уда-

51. При доказательстве второй теоремы благосостояния (о реализуемости Паретооптимума как равновесия) при невыполнении условия, что рассматриваемая точка — внутренняя, не удается показать, что ......................................, так как может оказаться что

........................................ (сформулируйте ответ в трех-пяти фразах и поясните, сказанное рисунком).

52. При доказательстве второй теоремы благосостояния (о Парето-оптимальности равновесных распределений) при невыполнении условия локальной ненасыщаемости, не удает-

53. Пусть два потребителя (потребление первого обозначим x, потребление второго обозначим z) в классической ситуации обмена имеют функции полезности

200