
Бусыгин
.pdf
301
Основное условие, гарантирующее эквивалентность моделей Эрроу—Дебре и Раднера, — наличие возможности переносить покупательную способность из одного состояния мира в другое. При этом вовсе не обязательно требовать, чтобы имелись все активы Эрроу. Для того, чтобы эта возможность существовала, достаточно, в частности, чтобы имелись все активы Эрроу, выраженные в 1-м благе, и только они (благо 1 — счетная единица, numeraire):
C = {(1, s) | s S}.
Проанализируем равновесие Раднера с таким набором активов. При анализе удобно использовать следующие обозначения: q1s = qs, zi1s = zis.
Заметим, что арбитраж в этой экономике возможен тогда и только тогда, когда qs и p1s имеют разные знаки или же qs = 0 хотя бы для одного состояния мира s. Мы будем далее предполагать, что 1-е благо нужно всем потребителям во всех состояниях мира, т.е. функции полезности строго возрастают по потреблению 1-го блага в каждом состоянии мира. Тогда в равновесии Раднера p1s > 0 s S. При этом арбитраж возможет тогда и только тогда, когда qs <0 хотя бы для одного состояния мира s. Соответствующий план арбитража построить достаточно просто — он должен сводится к покупке актива Эрроу, соответствующего состоянию s. Невозможность арбитража эквивалентна условию q> 0.
Торговля в первом периоде в подобной экономике фактически означает, что продаются или покупаются начальные запасы 1-го блага таким образом, чтобы во 2-м периоде, торгуя скорректированными запасами, получить доход, достаточный для покрытия расходов, связанных с приобретением равновесного потребительского набора x`, соответствующему равновесию Эрроу—Дебре. То есть торговля в первом периоде представляет собой «перераспределение покупательной способности» потребителя между состояниями мира с избыточной и недостаточной покупательной способностью.
Доказательства следующих двух теорем, проводящих параллели между равновесием Раднера и равновесием Эрроу—Дебре, демонстрируют правильность такой интерпретации равновесия Раднера при C = {(1, s) | s S}.
Теорема 7.
Пусть в экономике Эрроу функции полезности строго возрастают по потреблению 1-го блага в каждом состоянии мира, и (p`, x`) — равновесие Эрроу—Дебре в этой экономике. Тогда существует портфель активов Эрроу z-, выраженных в 1-м благе, а также цены активов q- такие, что (p`, q-, x`, z-) — равновесие Раднера с C = {(1, s) | s S}.
Доказательство.
Возрастание функции полезности по первому благу гарантирует положительность цен этого блага в равновесии Эрроу—Дебре в каждом состоянии мира (p`1s > 0 s S).
Дефицит, связанный с потреблением в состоянии мира x`is потребительского набора x`is , в ценах p` составляет величину dis = p`s(x`is – ωis). Тогда величину дефицита dis потребитель i
может покрыть, выбирая величину -zis равной d`is. Такой выбор -zis гарантирует, что вы-
p1s
полнены бюджетные ограничения второго периода задачи потребителя i в модели Раднера:
p`sx`is = p`sωis + p`1s-zis,
301

302
Заметим, что выполняется соотношение Ûdis = 0 (бюджетное ограничение потребителя i в
s S
модели Эрроу в равновесных ценах). Если выбрать в качестве цены актива (1, s) цену пер-
вого блага в состоянии мира s, т.е. -qs = p`1s, то соотношение Ûdis = 0 гарантирует выполне-
s S
ние бюджетного ограничения первого периода задачи потребителя i в модели Раднера.
Таким образом, (x`i, z-i) — допустимое решение в задаче (2) при ценах p` и q-. Покажем, что оно также является оптимальным решением. Предположим, что есть другое допустимое решение задачи (2), (x`i, z`i), которое дает i-му потребителю более высокую полезность. Так как (x`i, z`i) допустимо, то
Ûp`1sz`is <0,
s S
p`sx`is <p`sωis + p`1sz`is.
Сложив, получим
Ûp`sx`is <Ûp`sωis,
s S s S
что означает, что x`i — допустимое решение задачи (1), которое более предпочтительно для потребителя, чем x`i. Противоречие.
Проверим, что s S выполнены балансы активов:
Û-zis = Ûdis = Ûp`s(x`is – ωis) = p`s Û(x`is – ωis) = 0. |
|||
i I |
i Ip`1s i I |
p`1s |
p`1s i I |
Последнее равенство следует из балансов благ.
*
Для обратного утверждения нельзя в общем случае взять p-= p`, поскольку в равновесии Раднера цены p-s в каждом состоянии мира s можно умножить на произвольный положительный множитель, и при этом рассматриваемое состояние останется равновесием. Таким образом, требуется взять p`s = λsp-s , где λs — некоторый положительный множитель.
Теорема 8.
Пусть в экономике Эрроу функции полезности строго возрастают по потреблению 1-го блага в каждом состоянии мира, и (p-, q-, x-, z-) — равновесие Раднера в этой экономике с
C = {(1, s) | s S}. Тогда существует вектор цен p`, такой что (p`, x-) — равновесие Эр- роу—Дебре.
Доказательство.
Возрастание функции полезности по первому благу гарантирует положительность цен этого блага в равновесии Раднера в каждом состоянии мира. Кроме того, для каждого потребителя i выполнены (как равенства) бюджетные ограничения 1-го и 2-го периодов:
Û-qs-zis = 0,
s S
p-sx`is = p-sωis + p1s-zis.
Выберем p`s следующим образом,
302

303
p`s = --qs p-s.
p1s
Тогда
p`sx`is = p`sωis + qs-zis.
Складывая эти соотношения для всех состояний мира с бюджетным ограничением 1-го периода, убеждаемся, что при ценах p` выполняется бюджетное ограничение в модели Эрроу:
Ûp`sx`is = Ûp`sωis. s S s S
Таким образом, x`i — допустимое решение задачи потребителя (1). Покажем, что оно является оптимальным.
Пусть это не так, и x`i — другое допустимое решение задачи (1), с более высоким значением полезности. Так как x`i допустимо, то
Ûp`sx`i <Ûp`sωis.
s S s S
Тогда можно подобрать портфель активов, z`i, такой что (x`i, z`i) — допустимое решение задачи потребителя (2) в модели Раднера при ценах p и q. Для этого, как и в доказательстве предыдущей теоремы, можно выбрать z`is так, чтобы покрыть бюджетный дефицит в
соответствующем состоянии мира, dis = p-s(x`is – ωis), т.е. z`is = -pdis. При этом
1s
|
|
q |
|
|
Û-qsz`is = Û |
-s |
p-s(x`is |
– ωis) = Ûp`s(x`is – ωis)<0, |
|
-p |
||||
s S |
s S 1s |
s S |
||
т.е. выполнено бюджетное ограничение 1-го периода. Бюджетное ограничение 2-го периода выполнено в силу определения z`is. Получили противоречие.
*
Пример 4.
Рассмотрим модель Раднера с двумя состояниями мира, s = R, S, двумя благами, k = A, B двумя потребителями и возможными активами Эрроу, отмеченными в таблице. Они выражены в благе A.
|
s = R |
s = S |
k = A |
|
|
k = B |
|
|
|
|
|
Ожидания потребителей по поводу вероятностей состояний мира совпадают и равны
µR = µS = 1/2.
Предпочтения потребителей также одинаковы и элементарные функции полезности равны:
ui(xA, xB) = ln(xA) + ln(xB), i = 1, 2.
Начальные запасы указаны в нижеследующей таблице.
303

304
|
|
ω1 |
|
ω2 |
ωΣ |
|
|
A |
B |
A |
B |
A |
B |
s = R |
2, |
0 |
0, |
2 |
2, |
2 |
s = S |
2, |
2 |
0, |
0 |
2, |
2 |
С точки зрения начальных запасов в этом примере нет системного риска.
Задача потребителя i = 1, 2 равновесия Раднера этой экономики имеет следующий вид:
Ui = 12 (ln(xiAR) + ln(xiBR)) + 12 (ln(xiAS) + ln(xiBS)) → max xi,zi
qRziR + qSziS <0,
pARxiAR + pBRxiBR <pARωiAR + pBRωiBR + pARziR , pASxiAS + pBSxiBS <pASωiAS + pBSωiBS + pASziS .
Найдем равновесие Раднера в этом примере, пользуясь его взаимосвязью с равновесием Эрроу—Дебре. Поскольку нет системного риска, то в равновесии потребление обоих потребителей не зависит от состояния мира:
xiAR = xiAS, xiBR = xiBS.
Отношение цен одного и того же блага в двух состояниях, должно быть равно отношению вероятностей:
pAR |
µA |
|
0,5 |
pBR |
|||
|
= µB |
= |
0,5 |
= 1 = |
|
. |
|
pAS |
|
pBS |
|||||
Можно проверить, что в равновесии Эрроу—Дебре
x1AR = x1AS = x1BR = x1BS = 3/2.
x2AR = x2AS = x2BR = x2BS = 1/2.
pAR = pAS = pBR = pBS (можно выбрать = 1).
Положим qR = pAR = 1 , qS = pAS = 1. Для того, чтобы получить равновесие Раднера, нужно еще вычислить zis:
d1R = pR(xiR – ωiR) = – 12 + 32 = 1.
z = d1R = 1 = 1.
1R pAR 1
Аналогично d1S = –1.
d –1
z1S = p1S = 1 = –1.
AS
Для второго потребителя характеристика его портфеля активов определяется из баланса активов:
z2R = –1, z2S = 1.
304
|
|
305 |
|
|
|
|
|
|
ω |
|
ω |
|
|
|
@S |
|
S |
|
x |
|
|
x- |
S |
3/2 |
-R |
3/2 |
|
|
|
|
|
|
|
||
|
s = R |
|
s=S |
|
|
|
ω |
ω |
|
|
|
|
R |
@R |
|
|
|
|
3/2 |
3 |
1 |
3/2 |
|
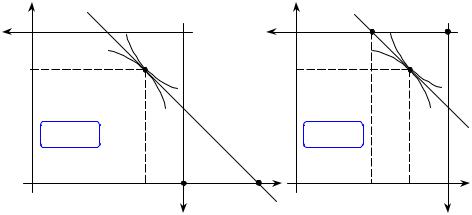
Рисунок 75. Иллюстрация к примеру 4 |
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим теперь модель Раднера, в которой активы не обязательно являются активами Эрроу. Для упрощения анализа будем предполагать, что все активы выражены только в первом благе. Поскольку доходности по остальным благам при этом равны нулю, то соответствующие коэффициенты можно не рассматривать. При этом будем использовать следующие обозначения: as = {asc}c — вектор, составленный из доходностей всех активов в состоянии мира s, A= {as}s — матрица, составленная из доходностей всех активов во всех состояниях мира.
Хотя в такой экономике могут быть довольно сложные активы, но они фактически сводятся к набору элементарных активов (активов Эрроу). Соответственно, цену любого (сколь угодно сложного) актива можно вычислить через цены активов Эрроу, даже если таких активов в экономике нет. Для доказательства этого факта мы опять воспользуемся тем, что в равновесии Раднера арбитраж невозможен.
Рассмотрим, что означает в такой экономике невозможность арбитража. Переформулируя определение, арбитраж невозможен, если не существует такого плана арбитража ∆z, что q∆z <0, и для любого состояния мира s S выполнено p1sas∆z>0, причем хотя бы для одного состояния мира неравенство строгое. Если p1s > 0 в любом состоянии мира, то последнее неравенство эквивалентно as∆z>0. Такая переформулировка означает невозможность составить допустимый план арбитража (не требующий увеличения чистых расходов на покупку активов), такой что он приводит к приросту доступного потребителю количества 1-го блага по крайней мере в одном состоянии мира и не уменьшает эту величину в других состояниях мира. Формально возможность арбитража при ценах активов q записывается следующим образом:
∆z: q∆z <0 и A∆z >≠0.
Для доказательства того факта, что цены активов можно разложить по ценам активов Эрроу требуется также дополнительное предположение о том, что матрица доходностей активов обладает следующим свойством:
∆z: A∆z >≠0. |
( ) |
Это свойство означает, что арбитраж в принципе возможен, если не учитывать бюджетное ограничение 1-го периода: можно подобрать план арбитража такой, что любом состоянии мира as∆z>0 и хотя бы для одного состояния неравенство строгое. (Ясно, что при равновесных ценах активов такой план арбитража должен потребовать увеличения чистых расходов на приобретение активов: q∆z > 0).
305

306
Теорема 992.
(i)Пусть A — матрица доходностей активов, удовлетворяющая предположению ( ), а q — цены активов, при которых арбитраж невозможен. Тогда существует вектор π>≠0, такой что q= πA.
(ii)Пусть цены активов можно представить в виде q= πA, где π> 0. Тогда при ценах активов q арбитраж невозможен.
Доказательство.
Предположим, что не существует вектора π>0, такого что q= πA. Это означает, что выпуклое замкнутое множество
V = {v| v= πA, π Ês^ },
не содержит вектор q. Простроим на основе этого «прибыльный» план арбитража, и придем к противоречию с предположением о том, что арбитраж невозможен.
По теореме о разделяющей гиперплоскости существует вектор ∆z′, такой что q∆z′ < c и v∆z′ >c, v V. Поскольку V — конус, то константу c можно положить равной нулю. При этом уравнение v∆z′ = 0 задает опорную гиперплоскость к конусу V, проходящую через его вершину. Поскольку as V, то as∆z′ >0 s, т.е. A∆z′ >0.
Вектор ∆z′ не обязательно дает требуемый план арбитража, поскольку не исключается случай A∆z′ = 0, когда в любом состоянии мира план арбитража ∆z′ не приводит к изменению дохода. Но может оказаться возможным несколько скорректировать ∆z′ и получить выгодный план арбитража. Возьмем произвольный план арбитража ∆z″, такой что A∆z″ > ≠0. (Должно выполняться q∆z″> 0, то есть этот план потребует увеличения чистых расходов на приобретение активов, иначе мы сразу получим, что арбитраж возможен). На основе ∆z′ и ∆z″ можно построить комбинированный план ∆z = ∆z′+ λ∆z′′, где λ — достаточно малое положительное число, такой что q∆z <0 и A∆z >≠0. Таким образом, получили противоречие с невозможностью арбитража, и доказали, что требуемый вектор π>0 существует.
Ясно, что π≠0, поскольку π= 0 возможно только при q= πA= 0, что противоречит невозможности арбитража при ценах q.
(ii) Пусть q= πA, где π> 0, и пусть ∆z — план арбитража, такой что A∆z >≠0. Тогда q∆z= πA∆z> 0. Таким образом, одновременное выполнение условий q∆z <0 и A∆z >≠0 невозможно.
*
Требуемое для доказательства условие ( ) верно при многих достаточно естественных предположениях на матрицу A. В частности, достаточно, чтобы матрица A имела ранг, равный количеству состояний мира, другими словами, чтобы вектора as были линейно независимы. Другой случай, когда можно легко построить ∆z″ — когда хотя бы один из активов не приносит отрицательного дохода ни в одном состоянии мира, а по крайней мере в одном приносит положительный доход (например, актив Эрроу). Тогда соответствующий план арбитража может заключаться в том, чтобы приобрести единицу такого актива (все компоненты вектора ∆z″ равны нулю, кроме компоненты, соответствующей
92 Фактически, это переформулировка в терминах рассматриваемой модели известной «леммы Фаркаша» из теории линейных неравенств.
306

307
данному активу, которая равна единице). В дальнейшем мы, как правило, будем предполагать, что матрица доходностей активов обладает свойством ( ).
Поскольку при равновесных ценах q арбитраж невозможен, то из доказанной теоремы следует, что можно представить равновесные цены активов в виде q= πA. Отдельный элемент вектора π, πs, можно интерпретировать как цену актива Эрроу (1, s).
Если матрица A имеет ранг, равный количеству состояний мира s^, то такой вектор π определяется однозначно. Можно выбрать s^ активов с линейно независимыми векторами доходностей и сформировать из них матрицу A^ , при этом π= qA^ –1. В противном случае удовлетворяющих этому соотношению векторов π может быть бесконечно много. Например, если в экономике есть только активы Эрроу, выраженные в 1-м благе, но не для всех состояний мира, то цены активов Эрроу для отсутствующих активов (1, s) можно выбрать произвольным образом.
Для каждой матрицы доходностей активов A можно задать подпространство активов, как подпространство, натянутое на вектора, соответствующие доходностям активов в разных состояниях мира:
l(A) = {w | w = Az, z Êc^}.
Вектор z здесь можно интерпретировать как портфель активов (поскольку речь идет об объективной характеристике системы активов, то индекс потребителя не пишется), а отдельный элемент вектора w, ws , — как доход от этого портфеля в состоянии мира ws (выраженный в количестве 1-го блага). Таким образом l(A) — это множество тех доходов, которые можно получить при некотором выборе портфеля z.
Для равновесий Раднера существенным является именно это подпространство активов, а не матрица A, по которой оно строится. Покажем это, доказав, что если l(A) = l(A′), то из равновесия Раднера с матрицей доходностей активов A можно сконструировать равновесие Раднера с матрицей доходностей активов A′. В доказательстве мы воспользуемся полученным выше представлением вектора цен активов в виде q= πA.
Теорема 10.
Пусть в экономике Эрроу функции полезности строго возрастают по потреблению 1-го блага в каждом состоянии мира, и (p, q, x, z) — равновесие Раднера в этой экономике, где все активы выражены в 1-м благе, и A — матрица их доходностей, удовлетворяющая предположению ( ). Тогда если A′ — другая матрица доходностей, такая что l(A) = l(A′), то существует портфель активов z′ и цены активов q′ такие, что (p, q′, x, z′) — равновесие Раднера с матрицей доходностей A′.
Доказательство.
Поскольку цены q соответствуют равновесию Раднера, и предпочтения локально ненасыщаемы, то при этих ценах невозможен арбитраж. Предположение ( ) гарантирует при этом, что существует вектор π= {πs}s, такой что q= πA.
В качестве цен активов q′ в конструируемом равновесии возьмем πA′.
Построим теперь z′. Поскольку Azi l(A) и l(A) = l(A′), то Azi l(A′). Другими словами, для любого zi существует вектор zi′, такой что A′z′i = Azi. Для каждого набора zi, i =
1, ..., m – 1 возьмем такой z′i. Кроме того, выберем zm′ так, чтобы выполнялся баланс активов:
307

308
m–1
zm′ = –Ûz′i.
i=1
Поскольку Ûzi = 0, то A′zm′ = Azm.
i I
Покажем теперь, что (p, q′, x, z′) — равновесие Раднера с матрицей доходностей A′. На-
бор (xi, z′i) допустим в задаче i-го потребителя при ценах p, q′ и матрице доходностей A′, поскольку
q′z′i = πA′z′i = πAzi = qzi <0.
и
pxi <pωi – p1saszi = pωi – p1sa′sz′i.
Покажем, что (xi, z′i) является оптимальным решением. Пусть это не так, и (x`i, z`′i) — другое допустимое решение задачи i-го потребителя при ценах p, q′ и матрице доходностей A′, с более высоким значением полезности. Тогда, следуя рассмотренной выше схеме, можно подобрать портфель активов, z`i, такой что (x`i, z`i) — допустимое решение задачи потребителя при ценах p и q и матрице доходностей A. Поскольку x`i дает потребителю более высокую полезность, чем xi, то это противоречит оптимальности (xi, zi) при ценах p и q и матрице доходностей A.
*
Замечание. Таким образом, каждому равновесию Раднера в экономике с множеством активов с матрицей доходностей A соответствует равновесие Раднера в экономике с множеством активов с матрицей доходностей A′ с теми же планами потребления и ценами благ. Верно и обратное, если матрица A′ удовлетворяет предположению ( ).
Если матрица доходностей A имеет ранг, равный количеству состояний мира s^ (т.е., если структура доступных активов является достаточно «богатой»), то
l(A) = l(I),
где I — единичная матрица размерности s^×s^. Матрица доходностей I соответствует случаю, когда C = {(1, s) | s S}, то есть когда все активы в экономике являются активами Эрроу, выраженными в 1-м благе. Поэтому при выполнении этого условия — полного ранга матрицы A — верны аналоги доказанных ранее для случая A= I теорем об эквивалентности равновесий Эрроу—Дебре и Раднера.
Теорема 11.
Предположим, что в экономике Эрроу функции полезности строго возрастают по потреблению 1-го блага в каждом состоянии мира. Кроме того, будем предполагать, что все доступные потребителям в равновесиях Раднера активы выражены в 1-м благе, и матрица их доходностей A имеет ранг, равный количеству состояний мира.
(i)Пусть (p`, x`) — равновесие Эрроу—Дебре в этой экономике. Тогда существует портфель активов z- и цены активов q такие, что (p`, q, x`, z-) — равновесие Раднера.
(ii)Наоборот, пусть (p, q, x-, z-) — равновесие Раднера в этой экономике. Тогда существует вектор цен p`, такой что (p`, x-) — равновесие Эрроу—Дебре.
Доказательство.
Данное утверждение является следствием Теорем 7, 8 и 10.
308

309
На основании равновесия Эрроу—Дебре можно сконструировать равновесие Раднера с матрицей доходностей активов I, а на основании последнего — равновесие Раднера с матрицей доходностей активов A. Наоборот, на основании равновесия Раднера с матрицей доходностей активов A можно сконструировать равновесие Раднера с матрицей доходностей активов I, а на основании последнего — равновесие Эрроу—Дебре.
*
Замечание. Пользуясь свойствами равновесия Эрроу—Дебре, получим важное следствие из данной теоремы: если матрица активов в модели Раднера имеет полный ранг, то каждое равновесие в такой модели Парето-оптимально. С другой стороны, если матрица активов неполного ранга, то возникает проблема неполноты рынков, и в общем случае равновесие Раднера неоптимально.
Задачи
5. Рассмотрим экономику с двумя потребителями (i = 1, 2), двумя состояниями мира (Sun, Rain) и двумя (физическими) благами (Apples, Bananas) запасы которых в состоянии мира S у 1-го потребителя — ω1S = (0; 0), у 2-го потребителя — ω2S = (3; 6), а в состоянии мира R у 1-го потребителя — ω1R = (5; 1), у 2-го потребителя — ω2R = (1; 2). Предположим, что предпочтения потребителей описываются функциями полезности Неймана— Моргенштерна с элементарными функциями полезности
u1 = –1/x1a – 1/x1b u2 = x2a + 4x2b
Предположим, что вероятность состояния мира S равна 2/3, а вероятность состояния мира
R — 2/3.
(1) Покажите формально, что состояние x1S = (2; 1), x1R = (2; 1), x2S = (1; 5), x2R = (4; 2), pa = (1; 2), pb = (4; 8) является равновесием Эрроу—Дебре.
(2) Как на основе равновесия Эрроу—Дебре сконструировать равновесие Раднера?
6. Рассмотрим экономику с двумя потребителями (i = 1, 2), двумя состояниями мира (Good, Bad) и двумя (физическими) благами (Apples, Cucumbers) запасы которых в состоянии мира G у 1-го потребителя — ω1G = (4; 4), у 2-го потребителя — ω2G = (2; 2), а в состоянии мира B — ω1B = (1; 1) и ω2B = (5; 5) соответственно. Предположим, что предпочтения потребителей описываются функцией полезности Неймана—Моргенштерна с элементарной функцией полезности вида
ui = ln xia + ln xic
Предположим, что вероятность состояния мира G равна 2/3, а вероятность состояния B — 2/3.
(1)Покажите формально, что состояние x1 = (3; 3; 3; 3), x2 = (3; 3; 3; 3), pG = (2; 2), pB = (1; 1),
является равновесием Эрроу—Дебре.
(2)Как на основе равновесия Эрроу—Дебре сконструировать равновесие Раднера?
7. Рассмотрим экономику с двумя потребителями (i = 1, 2), двумя состояниями мира (Sun, Rain) и двумя (физическими) благами (Apples, Bananas) запасы которых в состоянии мира S у 1-го потребителя — ω1S = (3; 3/2), у 2-го потребителя — ω2S = (3; 3/2), а в состоянии мира R у 1-го потребителя — ω1R = (3; 3/2), у 2-го потребителя — ω2R = (3; 3/2). Пред-
309
310
положим, что предпочтения потребителей описываются функциями полезности Нейма- на—Моргенштерна с элементарными функциями полезности
ui = ln xia + ln xib
Предположим, что субъективная вероятность состояния мира S для 1-го потребителя равна 2/3, а вероятность состояния мира R — 2/3. Субъективная вероятность состояния мира S для 2-го потребителя равна 2/3, а вероятность состояния мира R — 2/3.
(1) Покажите формально, что состояние x1S = (2; 1), x1R = (4; 2), x2S = (4; 2), x2R = (2; 1), pa = (1; 1), pb = (2; 2) является равновесием Эрроу—Дебре.
(2) Как на основе равновесия Эрроу—Дебре сконструировать равновесие Раднера?
8. Рассмотрите модель Раднера с двумя состояниями мира (R и S), с двумя благами (A и B) и системой активов, состоящей из всех возможных активов Эрроу. Пусть цены активов
равны (qaR, qaS, qbR, qbS) = (1; 2; 3; 4), а цены благ равны (2; 6) в состоянии R и (1; 3) состоянии S. Возможен ли при таких ценах арбитраж? Если возможен, то предложите план ар-
битража. Если невозможен, то объясните почему.
9.Рассмотрите модель Раднера с двумя состояниями мира (R и S), с двумя благами (A и B) и системой активов, состоящей из двух активов Эрроу, выраженных в благе A. Пусть
цены активов равны (qaR, qaS) = (1; 4). Возможен ли при таких ценах арбитраж? Если возможен, то предложите план арбитража. Если невозможен, то объясните почему.
10.Рассмотрите модель Раднера с двумя состояниями мира (R и S), с двумя благами (A и B) и системой активов, состоящей из двух активов, выраженных в благе A. Один актив дает 1 в состоянии R и 1 в состоянии S, а другой — 0 в состоянии R и 1 в состоянии S.
Выгоден ли план арбитража ∆z = (1; –1)? Предложите цены активов, при которых этот план арбитража не приводит к увеличению чистых расходов на покупку активов.
11. Рассмотрите модель Раднера с двумя состояниями мира (R и S), с двумя благами (A и B) и системой активов, состоящей из двух активов, выраженных в благе A. Один актив дает 1 в состоянии R и 1 в состоянии S, а другой — 0 в состоянии R и 1 в состоянии S. Пусть цены этих активов равны 4 и 1 соответственно. Найдите соответствующие «цены активов Эрроу» πR и πS. Что можно сказать по этим ценам о возможности арбитража?
12. Покажите, что равновесию Раднера могут соответствовать планы потребления, которые являются недопустимыми в задачах потребителя в модели Эрроу при любых равновесных ценах.
Задачи к главе
13. Известно, что потребитель в экономике с риском с полной системой рынков имеет строго вогнутую элементарную функцию полезности, зависящую от одного (физического) блага и заданную на неотрицательных количествах потребления. Что можно сказать об объемах потребления в разных состояниях мира, если цены блага в разных состояниях мира пропорциональны вероятностям? Рассмотрите либо общий случай, либо (для упрощения) дифференцируемую функцию полезности и 2 состояния мира.
310
