§ 3 Задачи для самостоятельного решения

Задача 1

Х и У независимые случайные величины.

f_x(x)=f_Y(y)=

Найти:1)P{YX}; 2)R[X;Y]; 3)M[X*Y]

Ответ:1)p{YX}=*dy=3/4+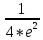;2)R[X;Y]=0;3)M[X*Y]=m_x*m_y

½*1=1/2

Задача 2

Случайная величина (Х;У) распределена равномерно в области,

ограниченной прямыми: У=Х; У=-Х; У=2.

Найти: 1)P{Y≤2X}; 2)Зависимы или нет Х и У; 3)M(m_x;m_y); 4)R[X;Y];

5)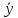(x)(условное математическое ожидание)

Ответ:1)P{Y2X}=1/4; 2)Х и У зависимы; 3)М(0;4/3); 4)R[X;Y]=0;

5)=

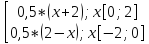
Задача 3

Случайная величина (Х;У) распределена равномерно в области(D),

ограниченной: У=Х; У=3Х; У=2/Х.

Найти:1)P{X*Y1}; 2)M[X*Y]; 3)

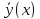
Ответ: 1)P{X*Y1}=1/2; 2)M[X*Y]=1; 3)=

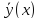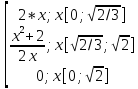
Задача 4

Двумерная случайная величина (Х;У) распределена равномерно

в области(D), где (D)-треугольник с вершинами О(0;0); А(1;0); В(0;1).

Найти: 1)f_XY(x;y); 2)f_X(x); f_y(y); 3)M(m_x;m_y); 4)_X; _Y; 5)_XY;

6)Зависимы или нет случайные величины Х и У?

Ответ:1) f_XY(x;y)=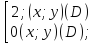

2)f_X(x)=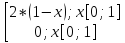; f_Y(y)=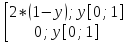

3)M(1/3; 1/3); 4)_x=_y=1/3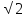≈0,236; 5)_XY=-0,5; 6) Х и У зависимы.

Задача 5

Двумерная случайная величина(Х;У) распределена равномерно

в области (D), где (D)- четверть эллипса: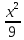+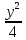=1; х0; у0.

Найти:1) f_XY(x;y); 2)f_X(x); f_y(y); 3)M(m_x;m_y); 4)_X; _Y; 5)_XY;

6)Зависимы или нет случайные величины Х и У?

Ответ:

5)_ХУ≈-0,3; 6)зависимы.

Задача 6

Дана функция плотности двумерной случайной величины (Х;У):

f_XY(x;y)=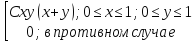

Найти:1)С; 2)f_x(x); f_y(y); 3)M(m_x;m_y); 4)_x;_y; 5)_XY; 6)Зависимы или нет Х и У?

Ответ: 1)С=3; 3)М(17/24; 17/24); 4)_Х=_у=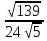≈-0.036; 6) зависимы.

Задача 7

Дана функция плотности двумерной случайной величины (Х;У):

f_xy(x;y)=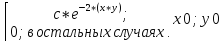

Найти:1)С; 2)f_x(x); f_y(y); 3)M(m_x;m_y); 4)_x;_y; 5)_XY; 6)Зависимы или нет Х и У?

Ответ:1) с=4; 3) М(0,5; 0,5); 4)_х=_у=0,5; 5)_ху=0; 6) независимы.

Глава 12. Закон больших чисел (предельные теоремы)

§ 1. Основные понятия и формулы

В курсе «Теория вероятностей» вы уже познакомились с предельными теоремами. Повторим основные теоремы.

Исторически теорема Бернулли – первая из доказанных теорем (1713 г.) (поведение относительной частоты по отношению к вероятности события) После теоремы Бернулли было доказано довольно большое число такого рода теорем, выясняющих поведение среднегоразличных случайных величин приnстремящейся к бесконечности. Суть их состоит в том, чтосреднее при неограниченном увеличении числа опытов теряет характер случайного и поэтому его поведение можно предсказать! Это положение, доказанное в ряде предельных теорем, называется законом больших чисел. Накопленный опыт отмечает хорошее согласие предельных теорем с реальной действительностью.

На предельных теоремах фактически основное вся математическая статистика – это средние величины, находимые из опытов. На практике мы чаще используем неравенства, на основании которых доказываются предельные теоремы

1. Неравенство Маркова

Пусть X – случайная величина (принимает неотрицательные значения) 0

• P{X≥}≤ M[X]/

• Р{X} 1 – M[X]/F()1 –M[X]/

[F(x)=P{Xx}]