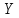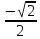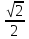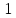- •Глава 1. Алгебра случайных событий
- •§1. Основные определения и понятия
- •Свойства противоположного события
- •2 Решение типовых задач
- •§3 Задачи для самостоятельного решения.
- •1) Построить пространство элементарных исходов
- •2) Указать состав подмножеств, соответствующих данным событиям
- •3) Выполнить указанные операции над данными событиями.
- •Глава 2 Классическое вероятностное пространство.
- •§1. Основные понятия и определения.
- •2) Все элементарные исходы равновозможные, т.Е.
- •Элементы комбинаторики.
- •§2. Решение типовых задач.
- •20 Футбольных команд, среди которых 4 призёра предыдущего первенства, по жеребьевке разбиваются на 4 занумерованные подгруппы по 5 команд.
- •Решение:
- •52 Карты раздаются четырём игрокам (каждому по 13 карт)
- •Решение:
- •4) Картошки, 5) наполеон, 6) невские.
- •Решение:
- •§3 Задачи для самостоятельного решения.
- •Глава 3 Относительная частота и её свойства
- •§1. Основные понятия.
- •Относительная частота события а:
- •4) Свойство устойчивости:
- •§2. Решение типовых задач
- •§3. Задачи для самостоятельного решения
- •Глава 4. Теоремы сложения и умножения вероятностей. Условная вероятность.
- •§1. Основные понятия
- •5)Теорема сложения для совместных событий:
- •6)Теорема умножения
- •7)Теорема о сумме совместных, но независимых в совокупности событий.
- •§2 Решение типовых задач.
- •Задача №6
- •Решение:
- •Глава 5. Формула полной вероятности. Формулы Байеса.
- •§1. Основные понятия
- •§2. Решение типовых задач. Задача 1
- •Задача 2
- •Задача 3
- •Задача 4.
- •Решение.:
- •Задача 5.
- •Решение:
- •Задача 6.
- •Решение.
- •Задача 8
- •Задача 9
- •§ 3 Задачи для самостоятельного решения
- •Задача 6.
- •Задача 7.
- •Задача 9.(новогодний аттракцион)
- •Задача 10.
- •Задача 11.
- •Задача 12.
- •Задача 13.
- •Задача 14.
- •Глава 6 Последовательность независимых испытаний
- •§1.Основные понятия
- •§2 Решение типовых задач
- •§3 Задачи для самостоятельного решения.
- •Задача 2.
- •Задача 3.
- •Глава 7. Одномерная случайная величина дискретного типа
- •1 Основные понятия
- •Полигон распределения
- •Основные дискретные распределения и их числовые характеристики
- •Задача2
- •Задача 3
- •Задача 7
- •Задача 8
- •Глава 8 Одномерная случайная величина непрерывного типа
- •§1 Основные понятия.
- •§2 Решение типовых задач
- •Задача 2
- •1)Основное свойство функции плотности:
- •Задача 3
- •Решение:
- •1)Основное свойство функции плотности:
- •Задача 4
- •Решение:
- •Задача5
- •Задача 6
- •§3 Задачи для самостоятельного решения
- •Задача 22
- •Задача 23
- •1. Строим график
- •§2 Решение типовых задач
- •§3. Задачи для самостоятельного решения
- •Глава 11. Непрерывная двумерная случайная величин
- •Условные математические ожидания
- •§ 2 Решение типовых задач
- •§ 3 Задачи для самостоятельного решения
- •Глава 12. Закон больших чисел (предельные теоремы)
- •§ 1. Основные понятия и формулы
- •1. Неравенство Маркова
- •2. Неравенство Чебышева
- •3. Неравенство Бернулли
- •§ 2. Решение типовых задач
- •§ 3. Задачи для самостоятельного решения
- •Глава 12. Нормальная случайная величина
- •§ 1. Основные понятия и формулы
- •§ 2. Решение типовых задач
- •§ 3. Задачи для самостоятельного решения
1. Строим график
Пусть
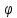 строго монотонна
строго монотонна
Находим:
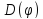 (область определения с учетом значения
с.в.
(область определения с учетом значения
с.в.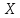 )
)
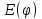 –множество
значений
–множество
значений
2.
Находим обратную функцию

3.
Вычисляем
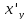 ,
,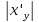
4.
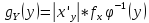 где
где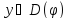
§2 Решение типовых задач
Задача 1
Случайная
величина
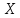 принимает значения
принимает значения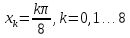 с вероятностью
с вероятностью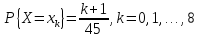 .
.
Описать
закон распределения случайной величины

Решение:

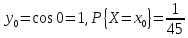 V
V
 1
1
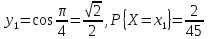 VV
VV
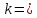 2
2
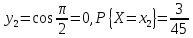 VVVV
VVVV
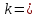 3
3
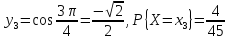 VVV
VVV
 4
4
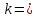 5
5
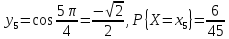 VVV
VVV
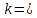 6
6
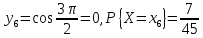 VVVV
VVVV
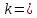 7
7
 VV
VV
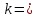 8
8
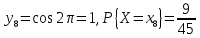 V
V
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 2.
X
ϵ
N (m,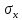 )
[X
распределенное по нормальному закону
с параметрами m
и
)
[X
распределенное по нормальному закону
с параметрами m
и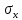 ]
]
Y=k X +b
Найти закон распределения с.в. Y.
Решение:
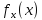 =
=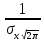
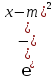 ,x ϵ(-∞;∞)
,x ϵ(-∞;∞)
Y=k x +b(строго монотонна)
X=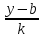 ,
,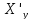 =
=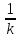 ,
,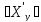 =
=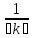
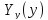 =
=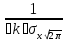
 y ϵ R
y ϵ R
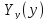 =
=
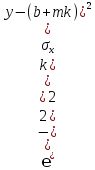
Y
ϵ N (mk+b); (∣k∣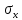 )
Вывод:
)
Вывод:
Y имеет нормальное распределение
M[Y] =mk+b
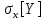 =
= k
k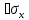
Задача 3.
С.В. X задана следующей функцией плотности:
f
(x) =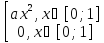
Y=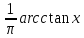 Найти
1)
Найти
1)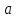 ;
2)
;
2)
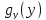
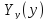 (функция
плотности Y)
(функция
плотности Y)
Решение:

1)Найдем
параметр
 ,
используя свойство функции плотности:
,
используя свойство функции плотности:
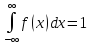
В
нашем случае: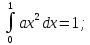 =>
=>
 =1;
=>
=1;
=>
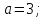
f
(x) =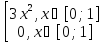
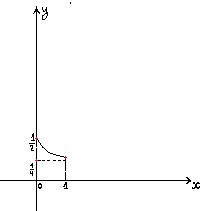
Y=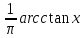
1) D[Y]=[0;1]область определения
2)
E(Y)=
[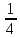 ;
;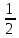 ]множество
значений(arcctan0=π/2;
arcctan1=π/4)
]множество
значений(arcctan0=π/2;
arcctan1=π/4)
3)φ
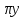 =
=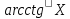 <=>
<=>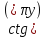 =X;
=X;
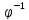 :
x
=
:
x
=
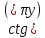
 =
=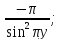
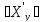 =
=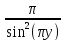
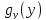 =
=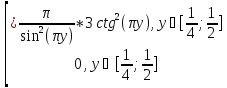
Задача 4.
f
(x) =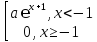
Y=-(X+1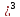 Найти: 1)
Найти: 1)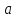 , 2)
, 2)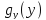
Решение:

1)Основное свойство функции плотности:
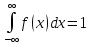
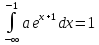
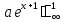 =1
=>
=1
=>
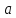 (1-
(1- )
=1 =>
)
=1 =>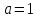 ;
;
f
(x) =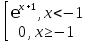
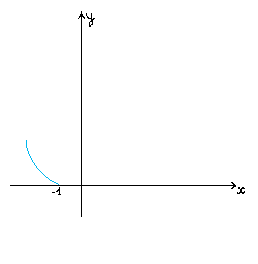
Y=
-(x+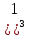
D[Y]=(- ∞;-1)
E(Y)= (0; ∞)
φ
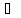
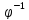 :
y =-(x+1
:
y =-(x+1 =>(x+1
=>(x+1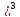 =-y=>x+1=
=-y=>x+1=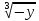
X=-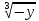 -1
-1
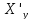 =
=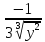 ,
, =
=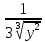
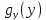 =
=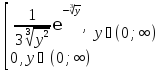

g(y)
Задача 5
Функция плотности задаётся следующей формулой:
f
(x) =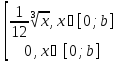
Y=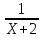 ;
;
Найти:
1) b;
2)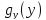 ;
;
Решение:
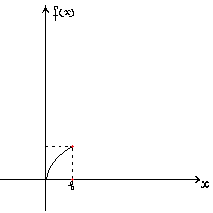
1)Основное свойство функции плотности:
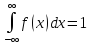
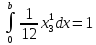 ;
;
 =1;
=1; =
=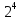 ;
=> b=8;
;
=> b=8;
f
(x) =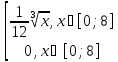
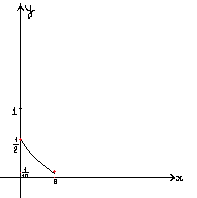
Y=
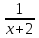
D[Y]=[0;8]
E(Y)=
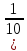 ;
; ]
]φ
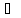
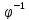 :
y =
:
y = =>
x+2=
=>
x+2=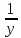 =>
x=
=>
x=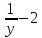
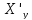 =
= ;
;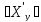 =
=

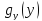 =
=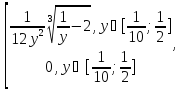
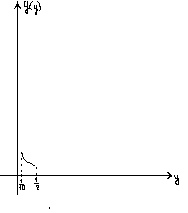
Задача 6
Дано: Х –стандартизированная нормально распределённая случайная величина:
χϵN(0,1) ƒ(x)=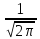
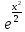
y=|x+1|-|2χ-1|
Найти gy(y)
Решение
Y=|x+1|-|2x-1|
y=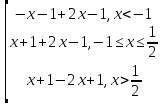
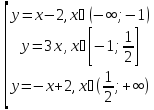

Три интервала монотонности
|
y=x-2 xϵ (-∞,-3] ↗ yϵ (-∞,-3] |
y=3x xϵ [-1;1/2] ↗ yϵ[-3;3/2] |
y=-x+2 xϵ [1/2;+∞) ↘ yϵ (-∞;-3/2] |
|
φ -1:x=y+2 |
φ -1:x=1/3y |
φ -1:x=-y+2 |
|
x’y=1 |x’|=1 |
x’y |x’|=1/3 |
x’y |x’|=1 |
Ответ:
9y(y)=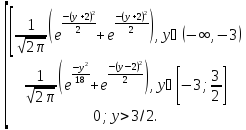
§3 Задачи для самостоятельного решения
Задача 1
Случайная величина χ задана рядом распределения
|
χ |
0 |
π/18 |
π/12 |
π/9 |
π/6 |
2π/9 |
π/4 |
5π/18 |
π/3 |
|
P |
0,01 |
0,1 |
0,09 |
0,1 |
0,09 |
0,2 |
0,2 |
0,2 |
0,01 |
Y=sin3χ Найти:1)ряд распределения Y 2)P{0,5<Y≤1}
Ответ: 1)
|
Y |
0 |
1/2 |
√2/2 |
√3/2 |
1 |
|
P |
0,02 |
0,3 |
0,29 |
0,3 |
0,09 |
P{0,5,<Y≤1}=0,68
Задача 2
χϵR (0;1/3) равномерное распределение
Y=3χ3 Найти: 1) gy(y) 2)M[Y]
Ответ:
gy(y)=
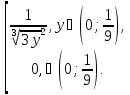
M[Y]=1/3
Задача3
χϵR(π/4;π/2) равномерное распределение
Y=ctgχ Найти: 1) 9y(y) 2)M[Y]
Ответ:
1) 9y(y)=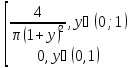
2)M[Y]= ln2
ln2
Задача 4
χϵR(0,e2) (равномерное распределение)
y=lnχ Найти 1) 9y(y); 2) M[y]
Ответ:
gy(y)=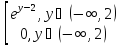
2)M[y]=1
Задача 5
χϵexp(λ) показательное распределение с параметром λ
y=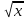 Найти: 9y(y)
Найти: 9y(y)
Ответ:
gy(y)=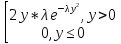
Задача 6
x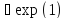 λ=1
– показательное распределение
λ=1
– показательное распределение
y=1/x2 Найти: ) 9y(y)
Ответ:
gy(y)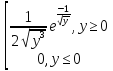
Задача 7
χϵR(-1;2)-равномерное распределение
y=χ2 Найти ) 9y(y)
Ответ:
gy(y)=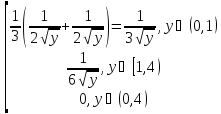
Задача 8 (распределение Коши)
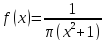
y=|2x+2|-|x-4|
Найти 9y(y)
Ответ
9y(y)=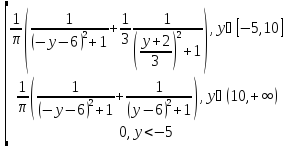
§4 Задачи для проведения самостоятельной работы
Задача 1
F(x)=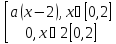
Y=√x
Найти 1)a; 2) 9y(y); 3)M[y]
Задача 2
f(x)=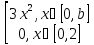
y=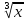 Найти
1)a, 2) 9y(y),
3)M[y]
Найти
1)a, 2) 9y(y),
3)M[y]
Задача 3
f(x)=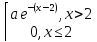
y=(x-2)2, Найти 1) a, 2) 9y(y)
Задача 4
f(x)=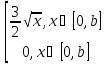
y=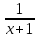
Найти 1)b; 2) 9y(y) 3)M[y]
Задача 5
f(x)=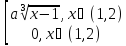
y=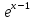
Найти 1)a; 2) 9y(y)
Задача 6
f(x)=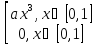
y= arctgx
arctgx
Найти 1)a; 2) 9y(y)
Глава 10 Дискретная двумерная случайная величина
§1 Основные понятия
Если каждому элементарному исходу опыта Ω ставится в соответствие упорядоченная пара чисел (х,у), то говорят, о двумерной случайной величине, которую обозначают (Х.У), где Х и У –одномерные
случайные величины. Если множество значений двумерной случайной величины конечно или счётно, то её можно задать таблицей распределения:
|
Х………..У |
У1 |
У2 |
… |
УJ |
… |
Yn |
|
X1 |
Р11 |
Р12 |
… |
Р1J |
… |
P1n |
|
Х2 |
Р21 |
Р22 |
… |
Р2J |
… |
Р2n |
|
… |
… |
… |
… |
… |
… |
.. |
|
XI |
PI1 |
PI2 |
… |
PIJ |
… |
PIn |
|
… |
… |
… |
… |
… |
… |
… |
|
Xm |
Pm1 |
Pm2 |
… |
Pmj |
… |
pmn |
Pij=P{(X=xi)*(Y=yj)};
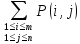 =1
=1
у
p1n
Pmn

yn















yj
pij













хi
xm
y2
p11


X















х2
y1
Pm1

х1








Функция распределения двумерной случайной величины (Х;У)- это числовая функция двух аргументов, которую обозначают F(x;у), при этом, в каждой точке (х;у) значение этой функции равно вероятности события:
((Хх)*(Уу)),
т.е. FXY(x;у)=P{(Xx)*(Yy)};
(вероятность попадания в юго-западный
«квадрант» )
х


у




Свойства функции распределения:
Область определения: (х;у)R2
Множество значений функции: 0≤F(х;у)≤1, при этом:
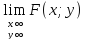 =1;
=1;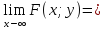 0;
0;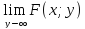 =0
=0Функция распределения не убывает по каждому из аргументов при фиксированном другом аргументе.
Для двумерной дискретной случайной величины справедлива формула:
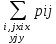
Условия согласованности
Постановка задачи
Пусть дискретная двумерная случайная величина задана таблицей распределения .
Найти одномерные законы распределения компонент Х, У.
Решение:
P{X=xi}= ;
i=1,
2,3,…, m.
P{Y=yj}=
;
i=1,
2,3,…, m.
P{Y=yj}=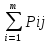 .(j=1,
2,…,n)
.(j=1,
2,…,n)
Для функции распределения условия согласованности определяются формулами:
FХ(х)=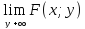 F(у)=
F(у)=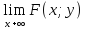
Независимые случайные величины
Случайные величины Х и У называются независимыми, если для любых
чисел х и у будут независимы события: A={Xx} и В={Y=y}Р(А*В)=Р(А)*Р(В)
Необходимые и достаточные условия независимости
Fху(х;у)=Fх(х)*Fy(y)
P{(X=xi)*(Y=yj)}=P{X=xi}*P{Y=yj} i=1, 2,…, m; j=1, 2,…, n
Числовые характеристики двумерной случайной величины
Центр распределения двумерной случайной величины (Х;У)- это неслучайная точка М(mx;my)
Корреляционный момент—числовая характеристика для количественной характеристики зависимости двух случайных величин: K[X,У]=M[(X-mx)*(Y-my)]
Для дискретной случайной величины справедлива формула:
K[X;Y]= *xi*yj
*xi*yj
По свойствам математического ожидания :
K[X;Y]=M[(X-mx)*(Y-my)]=M[X*Y-mx*Y-my*X+mx*my]=M[X*Y]-mx*M[Y]-my*M[X]+mxmy= M[X*Y]-mxmy
K[X;Y]= M[X*Y]-mxmy
M[X;Y]=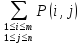 *xi*yj
*xi*yj
Заметим, что если Х и У независимые случайные величины, то
M[X*Y]=M[X]*M[Y] K[X;Y]=0
Однако., из условия, что К[X;Y]=0 , не следует в общем случае, что Х и У независимые случайные величины.
3.Коэффициент корреляции
Наряду с моментом корреляции, равную произведению размерностей Х и У, рассматривают безразмерную величину –коэффициент корреляции. который обозначается R[X;Y] и вычисляется по следующей формуле:
R[X;Y]=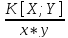
Свойства коэффициента корреляции
Если Х и У независимые случайные величины, то R[X;Y]=0.
-1≤ R[X;Y]≤1
R[X;Y]=1У=к*Х+в; если к>0,то R[X;Y]=1; если к0, то R[X;У]=-1.
Определение:
Если К[X;У]=0 ( R[X;Y]=0),то Х и У называются некоррелированными.
Из независимости Х и У следует некоррелируемость, но обратное утверждение в общем случае неверно.
Условные законы распределения
Аналогично
условным вероятностям :Р(В/А)=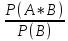 вводится понятие
вводится понятие
условного закона распределения.
Условным распределением случайной величины Х при условии У=уj
(j=1, 2,…,n) называется ряд, в котором вероятность соответствующая значению Х=хi (i=1,2,…,m), определяется как условная вероятность:
Pi/j=P{X=xi/Y=yj}=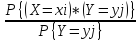 =Pij/pj
=Pij/pj
|
X |
X1 |
X2 |
… |
Xi |
… |
Xm |
|
P{X/Y=yj} |
P1/j |
P2/j |
… |
Pi/j |
… |
Pm/j |
Аналогично можно получить условное распределение случайной величины У при условии Х=хi(i=1, 2.,…,m)’
P{Y=yj
/X=xi}=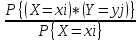
Если известен условный закон распределения случайной величины Х при
M[X/Y=yj]=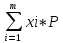 {X=xi/Y=yj}
j=1,2….,n
{X=xi/Y=yj}
j=1,2….,n
M[Y/X=xi]=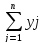 *P{Y=yj/X=xi}
, i=1, 2., ,m
*P{Y=yj/X=xi}
, i=1, 2., ,m
,Заметим,
что M[X/Y=yj]=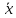 (y)-
функция от у
(y)-
функция от у
M[Y/X=xi]=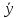 (x)-функция
от х
(x)-функция
от х
Условные математические ожидания называются соответственно:
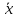 (y)—регрессия
Х по у,
(y)—регрессия
Х по у,
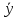 (x)---регрессия
У по Х
(x)---регрессия
У по Х
Заметим,
если Х и У независимые случайные величины,
то
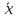 (y)=mx;
(y)=mx;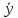 (x)=my
(x)=my