
векторная алгебра
.pdf
йцукенгшщзхъфывапролджэячсми |
тьбюйцукенгшщзхъфывапролджэ |
Лекции по теме «Векторная |
алгебра» |
ячсмитьбюйцукенгшщзхъфывапро |
Дисциплина «Линейная алгебра» |
лджэячсмитьбюйцукенгшщзхъфы |
Анисимова Н.П. |
вапролджэячсмитьбюйцукенгшщз |
хъфывапролджэячсмитьбюйцукен |
гшщзхъфывапролджэячсмитьбюй |
цукенгшщзхъфывапролджэячсмит |
Лекция 5. Глава 2. Элементы векторной алгебры.
§1.Множество векторов. Линейные операции над векторами.
П01.Определение вектора .Основные понятия.
Определение:
Вектором называется упорядоченная пара точек. АВ=а, где А – точка
начала, В—точка конца.
Геометрическая интерпретация: вектор – это направленный отрезок.
Основные характеристики вектора:
1) скалярная характеристика длина вектора, которую будем обозначать : АВ = а ;
2) направление
Для того чтобы задать вектор, достаточно знать:
1) длину и направление
или
2)координаты точки начала и конца
Определение равенства векторов:
Два вектора равны =
1) = (длины векторов равны)
2) вектора сонаправлены (  )
)
Определение нулевого вектора.
|
|
опр |
= |
|
|
|
|
О |
= |
||
|
любое направление |
||
Определение коллинеарных векторов.
Два вектора называются коллинеарными, если они лежат на параллельных прямых (можно сказать, что они параллельны).
Обозначение:
2

Различают: сонаправленные вектора, т. е. имеющие одно направление и противоположно направленные.
П02 .Сложение векторов.
Определение:
Суммой векторов и называется вектор , обозначаемый + ,
который можно получить по правилу треугольника:
сначала строим вектор и из конца построенного вектора строим вектор .Тогда вектор суммы соединяет начало первого вектора с
концом вектора .
a  b
b
a +b
Замечание:
1.Можно получить другое правило сложения в случае
неколлинеарных векторов.
3

Правило параллелограмма:
Из одной точки строим два данных вектора и достраиваем до параллелограмма.
Тогда диагональ этого параллелограмма, исходящая
из общей вершины , и будет вектором суммы данных векторов.
a
a+b
b
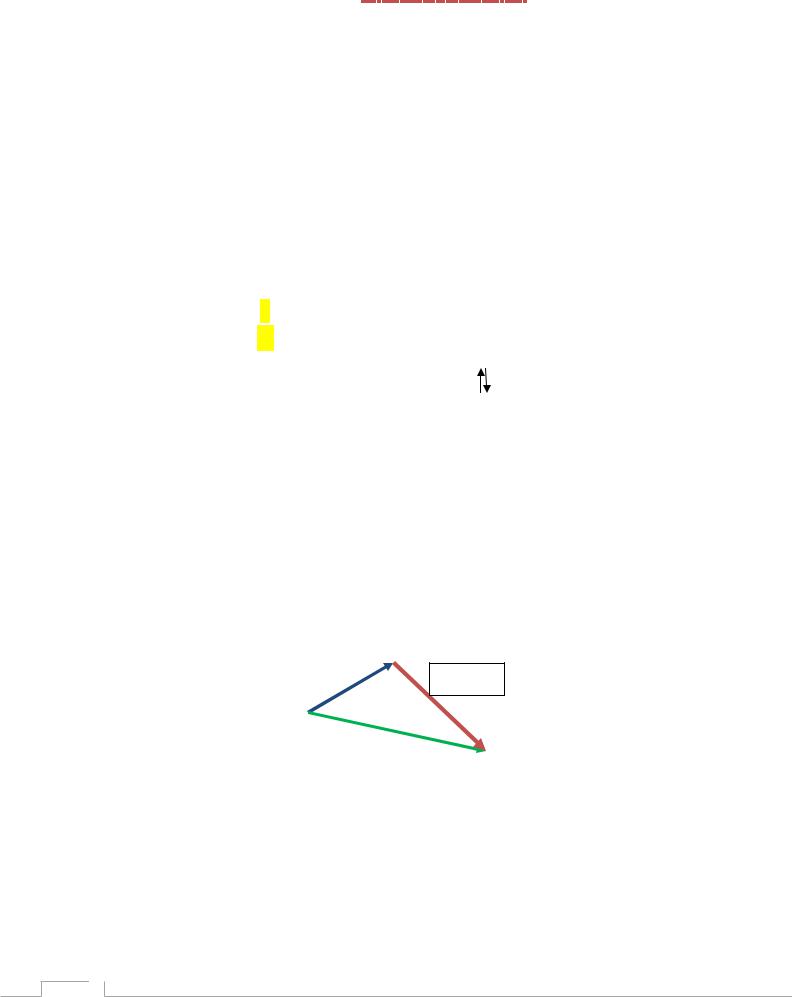
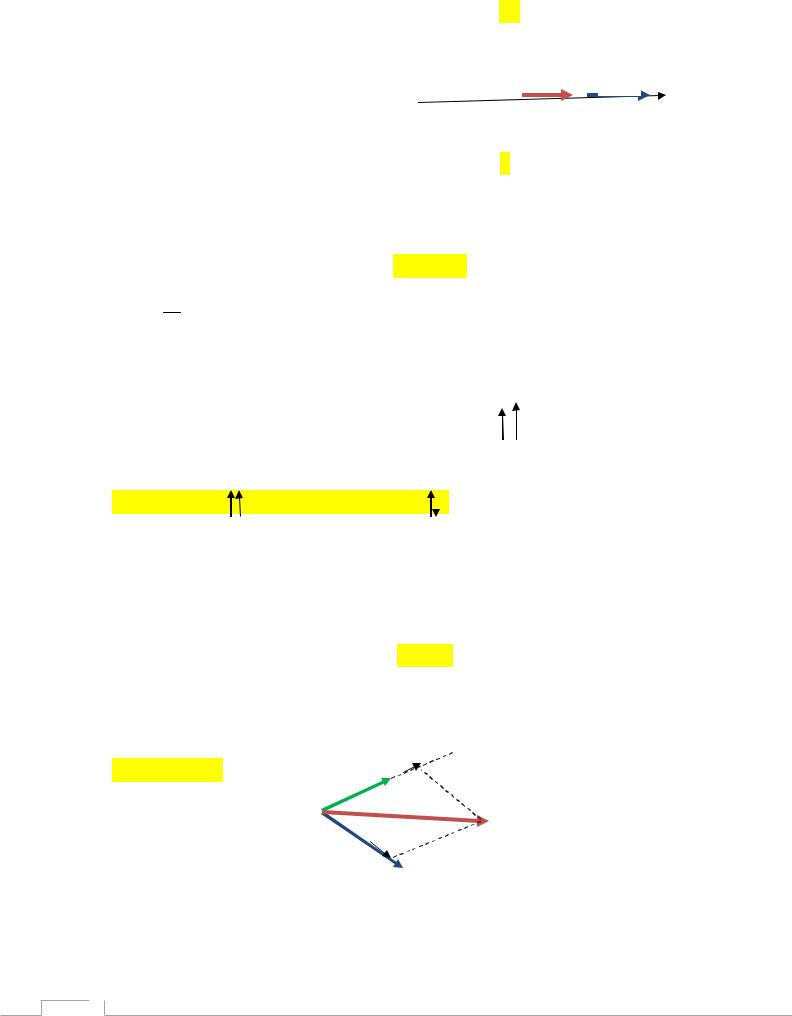
2.Правило суммы можно распространить на любое число слагаемых (правило ломаной).
Для получения суммы нескольких векторов нужно каждый следующий вектор начинать строить из конца предыдущего, а результирующий вектор будет соединять начало первого вектора с концом последнего.
b d c
a+b+c +d
4
Свойства сложения:
1) Свойство коммутативности.
Для любых векторов |
|
|
|
|
|
+ |
|
|
+ |
|
|
|||
2)Свойство |
ассоциативности: |
|
= |
|
|
|||||||||
|
|
|
и |
|
|
|
|
|
|
|||||
Для любых векторов |
|
|
|
|
|
+ |
|
|
|
|
||||
3)Свойство нулевого |
вектора |
: |
|
+ |
= |
+( + ) |
||||||||
|
, |
|
, |
|
|
|
|
|
|
|||||
a +0 = 0 +a для любого а
4)Существование противоположного вектора:
для любого а существует противоположный вектор, который
обозначают -а: +(−) = − + = .
Легко проверить, что |
|
|
|
|
5)( Свойство обратимости:= |
|
− , - ) |
+ = . |
|
Для любых векторов и |
существует вектор : |
|||
Вектор называется разностью и обозначается: |
= − |
|||
Чтобы получить вектор разности векторов и , нужно построить
оба вектора из одной точки и соединить концы векторов в сторону уменьшаемого вектора.
a
b −a
b
5

П03.Умножение вектора на скаляр.
Определение:
Для любого вектора а и числа R однозначно определён вектор,
обозначаемый а по следующему правилу:
1) а = * а
2)пусть а=с, тогда: при >0 с а,
а,
при 0 с а
а
при =0 с =
Свойства умножения вектора на скаляр.
1) *( а) = ( )а
2)( + ) = +
3)1 =
4)-1 = −
5)0 =
П04. Векторнаяискалярнаяпроекциявекторанаось.
Пусть дана ось L и вектор а. Спроектируем начало и конец данного
вектора на ось, т. е. опустим перпендикуляры. На оси L получим векторную проекцию данного вектора, начало и конец которого являются соответствующими проекциями начала и конца данного
вектора.
В
А
L
A1 B1
6
Если точка А –начало вектора АВ, то А1=ПрLА.
Если точка В –конец вектора АВ, то В1=ПрLВ.
А В векторная проекция вектора АВ на ось L (компонента вектора)
Орт оси это единичный вектор , который сонаправлен c осью L:
:
=
Теорема (необходимое и достаточное условие коллинеарности двух векторов)
Для того чтобы два вектора и были коллинеарны необходимо и
достаточно, чтобы существовало число , такое что справедливо равенство: = .
Доказательство:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Необходимость: |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
Пусть вектора коллинеарны |
|
|
|
|
||||||||||||||
1) |
|
вектора сонаправлены; пусть число = |
|
|
|
= |
|
|
|
||||||||||||||||||
|
|
; |
|
* |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
= |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|||||
2) |
|
вектора противоположно |
|
|
|
|
|
направлены; =- |
|
= |
|||||||||||||||||
с |
|
; |
= |
|
* = |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(необходимость доказана)
Достаточность:
7
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
то по определению операции умножения вектора на скаляр |
|||||
Если |
|
|
вектора, |
коллинеарны |
|
|
(достаточность выполнена) |
||
|
|
|
|
|
|||||
теорема доказана.
Важная информация.
Пусть дан вектор а. Обозначим а единичный вектор или орт вектора а
единичный вектор или орт вектора а
а =1; а  а.
а.
На основании предыдущей теоремы имеем формулу для нахождения орта данного вектора:
а =
= а
а
а
Вернёмся к векторной проекции вектора на ось.
Пусть А В векторная проекция АВ на ось L;
орт оси; т.к. А В L, то существует число х:
А В
В =х
=х (*)
(*)
Определение:
Число х, определяемое равенством (*) называется скалярной проекцией вектора АВ на ось L.
Замечание:
х= А В ; если А В  е − А В ; если А В
е − А В ; если А В 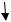 е
е
Теоремы о проекциях.
B
1. AB =ПрLAB cosφ
φ
A L
8

2.ПрL( + ) =ПрL +ПрL |
a |
b |
a +b L
a
3.ПрL = ПрL
a 
L
§2. Геометрическое пространство векторов.
П01. Линейная зависимость и независимость векторов.
Будем рассматривать множество векторов, в котором введены линейные операции, обладающие рассмотренными выше свойствами.
В этом случае говорят, что мы имеем линейное пространство векторов.
Определение:
Система векторов а; а;…;а называется линейно зависимой, если
найдутся числа: 1; 2;…; n (не все равные нулю):
1 + 2 +…+ n =∑ = (линейная комбинация векторов равна
нулевому вектору при условии, что не все числа i равны нулю).
Если |
∑ |
|
|
= тогда и только тогда, когда все числа |
i=0, |
i=1,2,…,n, то |
|||||
|
|
||||||||||
|
|
|
|
а; а;…;а Определение: |
|
|
|||||
система векторов |
|
называется линейно независимой. |
|||||||||
Система векторов |
|
называется базисом, если выполнены |
|||||||||
|
|
|
|
вектора линейно независимы, 2) любой вектор можно |
|||||||
два условия: 1) |
; ;…; |
|
|
|
|
|
|
||||
представить в виде линейной комбинации данных векторов , та.е. |
|||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Числа с1;с2;…;сn называют координатами вектора а в этом базисе.
Если в пространстве векторов существует базис, состоящий из «n» элементов, то говорят, что размерность пространства равна «n».
9
Имеем пространство векторов, обозначаемое Rn .
П02. Одномерное векторное пространство. |
а |
|
R1 Имеем числовую ось. |
R1 |
е
Пусть базис этого пространства будет вектор е
Т.к. любой вектор числовой оси коллинеарен е , то можно найти число
: а = е
( =± а ) координатавектораа вэтомбазисе.
е
Множествовектороввида: { }называют линейной оболочкой,
порожденной вектором |
|
|
|
|
|
||
Рассмотрим орт оси, которыйе |
обозначим ( |
L; |
|
|
. |
||
а |
|
|
|
находим по формуле: |
|||
Тогда |
=х ; где координату вектора в этом |
базисе |
|||||
= |
) |
|
|||||
х= а ; если а |
; |
x=- |
; если |
. |
П03. Двумерное векторное пространство.
R2 - это плоскость.
В качестве базисных векторов возьмём два неколлинеарных вектора
е и е
и е
а |
= 1 |
е |
|
+ |
|
2 |
е |
|
е |
|
|||||||||
|
а
е
10
