векторная алгебра
.pdf
Любой вектор а представлен в виде линейной комбинации базисных
векторов.
Тогда множество вида: { 1е
+ 2е
} – линейная оболчка порождённая векторами е и е .
Рассмотрим прямоугольную систему координат (х0у).
Обозначим орт оси абсцисс 
, а орт оси ординат 
.
Тогда система этих векторов образует естественный базис
;
.
у
A
y |
|
|||||
|
|
|
|
|||
|
j |
|
|
х |
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|||
|
O |
|
|
x |
||
i |
||||||
|
|
|
|
|
||
|
|
|
|
|
|
|
В естественном базисе имеем следующую формулу разложения вектора:
=x
+y
(разложение вектора по осям координат).
Допускается так же запись, где указываются только координаты вектора в естественном базисе: = = { , }
Заметим, что длина вектора находится через координаты вектора:
а = х
+ у
Т.к. координаты вектора – это проекции вектора на оси координат, то по свойству проекций, все линейные операции над векторами выполняются и над проекциями:
если = { ; }; = { ; }, то = + имеет координаты:
= { x1+ y1; x2+ y2}
11
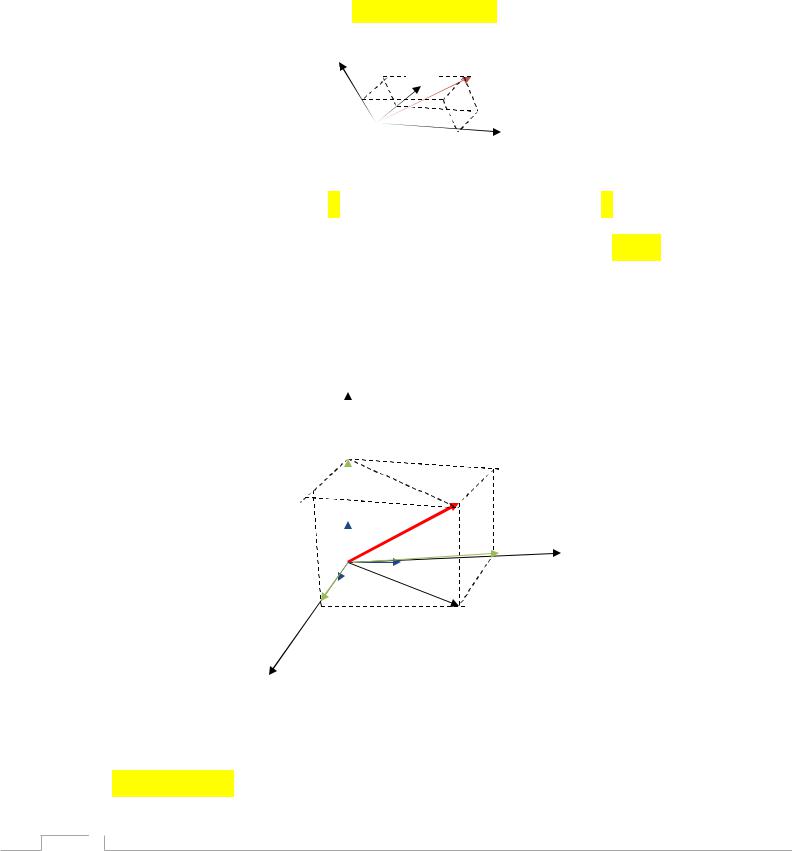
П04. Трёхмерное векторное пространство.
R3- трёхмерное пространство. В качестве базисных векторов можно взять любые три некомпланарных вектора (не лежащих в одной плоскости). Пусть это будут вектора е;е; е .
Любой вектор а представлен линейной комбинацией:
а= 1е
+ 2е
+ 3е
е
а
е
е
Рассмотрим прямоугольную декртову систему координат (0хуz).
Обозначим орт оси (OX) 
, орт оси (OY) 
, орт оси (OZ)
Тогда система этих векторов образует естественный базис
;
; .
z
z
k |
ȷ |
A |
|
|
|
|
|
|
y |
|
|||
0 |
|
|
|
у |
||
|
|
|
||||
|
||||||
|
ı |
|
|
|
|
x
х
Вестественном базисе имеем следующую формулу разложения вектора:
=x
+y
+z (разложение вектора по осям координат).
12
Допускается так же запись, где указываются только координаты вектора в естественном базисе: = = { , , }
Заметим, что длина вектора находится через координаты вектора:
а = х
+ у
+
Т.к. координаты вектора – это проекции вектора на оси координат, то по свойству проекций, все линейные операции над векторами выполняются и над проекциями:
если = ; ; ; = { ; ; }, то = + имеет координаты:
= { x1+ y1; x2+ y2 ; x3+ y3}
Замечание:
Если известны координаты начала и конца вектора АВ , т.е. А(х1;y1;z1);
B(x2;y2;z2), то координаты вектора находим по формуле:
={x2-x1; y2-y1;z2-z1}
Длина вектора находится тогда по формуле:
|
|
|
= |
( − ) +( − ) +( − ) |
|
|
|
|||||||||||||||||||||||||||||||||||||
Дано: = |
; = |
|
− |
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
+ ; |
A(-1;2;-3); B(1;2;1); = − . |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Найти: 1) |
|
|
|
|
|
. |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Решениес; : )с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
2;0;4} |
|
={5*2-3*2; 5*0-3*(-3); 5*4-3*4} |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
1) ={1+1;2-2;-1-3} |
|
|
|
= |
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
={4;9;8} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2) = √ |
+ |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
={ |
|
|
|
|
|
; |
|
√ |
|
|
|
|
; |
|
√ |
|
|
|
} |
|
|||||||||
|
|
|
|
|
=√ |
|
|
|
; |
|
|
√ |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Примечание: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Координаты единичного вектора (орта) называются направляющими
косинусами и обозначаются: { |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
( |
) |
|
+( |
|
|
) |
|
+( |
) |
|
= |
|
||||||||||||
при этом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
; |
|
|
} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13
§3 Скалярное произведение векторов и его свойства.
|
|
или( , ) |
Определение: |
и |
|
|
Скалярным |
векторов |
называется число, |
||||
произведением |
|
|||||
обозначаемое |
|
, которое вычисляется |
по формуле: |
|||
|
= |
|
|
|
|
( , |
|
) |
или |
|
= |
|
|
|
Пр = *Пр |
|
|
|
|
|
|
|
|
|
|
|
|
. |
( , )= |
b |
|
α |
a
Геометрические свойства скалярного произведения.
1.>0 900
2.0 900 1800
3.=
4. |
Если |
|
, |
то |
= |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
5. |
Скалярный |
квадрат |
|
= |
|
; если 2 |
|
|
|
то |
=- |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
а аа = а |
|
|
а |
|
|
|
= |
√ |
а |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= = =1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
; |
= |
|
; |
|
|
Примечание |
|
|
|
|
|
||||||||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Алгебраические свойства скалярного произведения.
1.=
2.( )=( ) = ( )
3.+ = +
1)(2 |
|
Замечание: |
2- 2 |
|
||
2 |
|
|
2 |
|||
+ |
|
) − |
|
= |
|
+ |
2)( + ) = +2 |
||||||
3) + = |
( + ) |
|
||||
14
Вычисление скалярного произведения через координаты вектора.
Если = + + ; = + + , то
|
x1*x2+y1*y2+z1*z2 |
(легко |
проверить |
непосредственным |
|
умножением |
с использованием свойств скалярного произведения) |
||||
|
= |
|
|
|
|
|
|
|
|
|
|
|
(формула для вычисления угла |
|
|
|
векторами) |
|
|
|
|
между |
|
|
|||||
= |
|
|
|
||||
Пример 1.
Дано: ∆АВС; A(2;-1;6); B(0;-4;5); C(9;-8;6).
Найти : угол при вершине В.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= ; |
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
={0-2; -4-(-1); 5-6} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
={-2;-3;-1}; |
|
|
= |
√ |
|
|
|
+ |
|
|
|
+ |
|
= |
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
={9-0;-8-(-4);6-5} |
|
={9;-4;1}; |
|
|
|
|
|
|
= √ |
|
+ |
|
|
+ |
|
=√ |
|
=7 |
√ |
|
. |
||||||||||||||||||||||||||||||
|
|
=-2*9+(-3)*(-4)+(-1)*1=- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
/ |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
= |
|
|
|
|
|
√ |
|
|
√ |
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
√ |
|
|
)≈ |
|
|
|
|
|
|
|
|
||||||||
|
= |
|
|
=- |
; |
|
|
|
|
|
B=arcos( |
|
|
100 89. |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
= |
|
|
− |
|
|
|
; |
= − |
|
Пример 2. |
|
|
|
; |
= |
;( ; ) = |
|||||||||||||||||||||||||||||
|
|
|
|
Дано: |
|
|
|
|
|
+ |
; |
= |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти: |
Пр( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:− |
) |
|
|
|
|
|
|
|
|
|
|
|||||||
15
Пусть с = − = ( |
− ) − (− + ) |
|||
|
|
|
|
|
В дальнейшем нам |
понадобится скалярное произведение: |
|||
|
= |
− |
||
= * * |
=4*3*(-0,5)=-6. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
= ( |
|
− |
)(− |
+ ) |
|
|
Пр |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
2+26 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
=-9*16-16*9+26*(-6)= |
-444 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
=-9 |
|
|
|
2-16 |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
= |
|
|
|
|
|
|
=(− |
+ ) = |
|
-4 |
|
+ |
|
|
|
|
|
= |
√ |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
=16+24+36=76 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
√ |
|
|
|
|
≈ |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Пр |
|
|
= |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
- |
50,93 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ : √ ≈-50,93
16
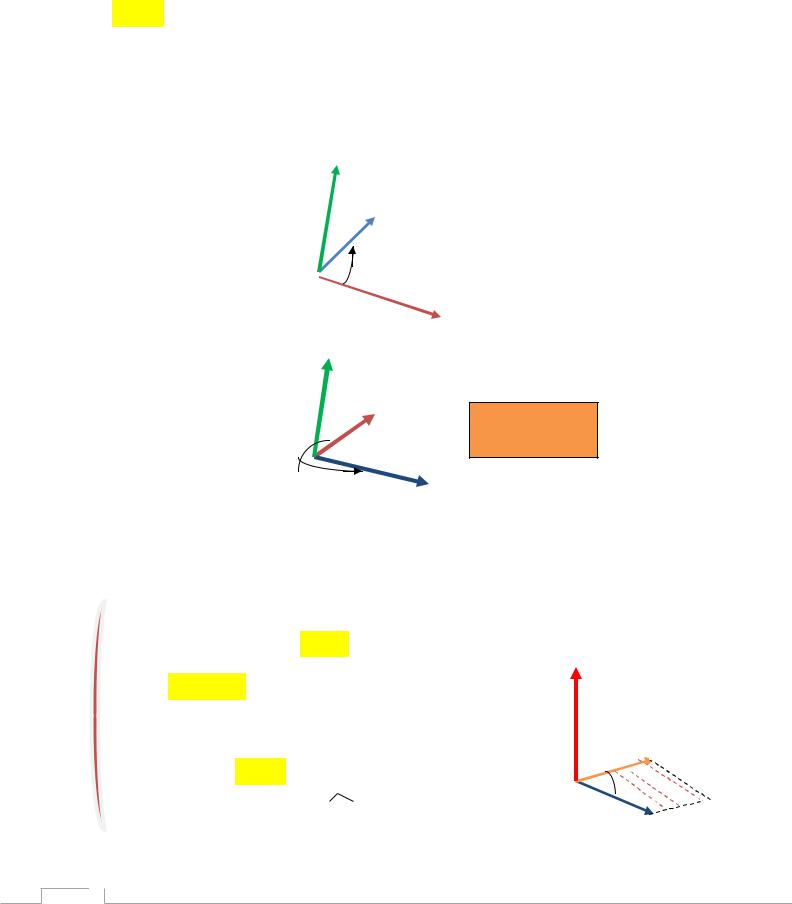
§4.Векторное произведение.
Определение правой (левой) тройки.
Рассмотрим три некомпланарных вектора, исходящих из одной точки:
;
; . Если смотреть из конца вектора с и поворот от первого вектора а
ко второму вектору против часовой стрелки будет выполняться по
наименьшему углу, то говорят, что эти вектора в данном порядке образуют правую тройку. В противном случае будем иметь левую тройку.
c
b |
Правая тройка |
a
c
Левая тройка
b
Определение векторного произведения.
Векторным произведением двух векторов и называется вектор,
который обозначают × .
a ×b
Пусть × = с. Тогда по определению имеем:
1) ; |
|
|
|
||||||
2)три вектора |
; |
|
; |
. |
образуют правую тройку. |
|
b |
||
3) |
|
× = |
* |
( ; ) |
a |
|
|||
|
|||||||||
|
|||||||||
17
Длина векторного произведения численно равна площади параллелограмма, построенного на векторах и
Заметим, если ,.то × =
Свойства векторного произведения.
!!!
Если ,то × = . В частности: × =
1. Антикоммутативность.
× = − ×
2. ( × ) = ( ) × = ×( )
3.Дистрибутивность
× + = × +( × )
Рассмотрим векторное произведение для орт координатных осей и результат занесём в таблицу.
× |
|
|
- |
|
- |
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
18
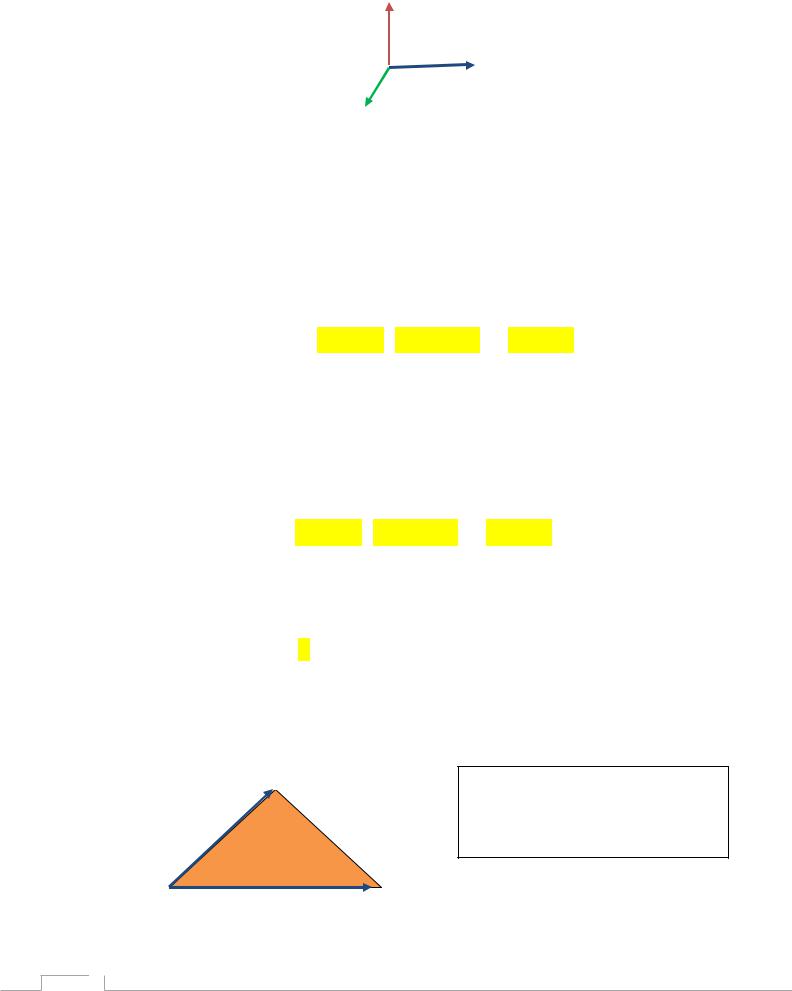
k
ȷ
ı
Пусть вектора заданы своими координатами.
Если = + + ; = + + , то
× =x1*y2* +x1*z2*(- )+y1*x2*(- )+y1*z2* +z1*x2* +z1*y2*(-)
× =(y1z2-z1y2) +(x1y2-y1x2) +(z1x2-x1z2)
Чтобы не запоминать эту формулу можно использовать символический определитель:
|
|
− |
+ |
|
× = |
= |
= |
=(y1z2-z1y2) +(x1y2-y1x2) +(z1x2-x1z2)
Пример 1.
Дано: ∆АВС; A(2;-1;6); B(0;-4;5); C(9;-8;6).
Найти S ∆ABC(площадь треугольника)
Решение:
В
S∆ABC=
b
1/2 s (параллелограмма)
А |
С |
a
19
AC = a; AB = b |
|
={9;-4;1}; |
|
|
={-2;-3;-1} |
|
|
||
∆ |
× |
|
|
× |
= |
|
− |
= |
|
S ABC=1/2 |
|
|
|
|
|
|
|||
−− −
|
− − − |
− − |
+ |
− − |
|
|
|
|||||||
= |
− |
|
|
|
− |
=7 +7 -35 |
|
|||||||
× =√ |
+ |
+ |
=21√ |
|
S |
∆ |
ABC= |
√ |
|
|
|
|
||
|
|
|
|
|||||||||||
|
|
|
|
|
||||||||||
Ответ: √ кв.ед.
Пример 2.
Дано: = − ; = +2 ; = |
; = ;( ; )=1500. |
Найти площадь параллелограмма , построенного на векторах и .
Решение:
Длина векторного произведения численно равна площади параллелограмма, построенного на векторах и
× |
= |
( − |
)× |
( |
+ |
2 |
|
)=6( |
× ) − ( × ) |
=12( |
× ) |
||
× = |
|
× =12 |
|
|
=12*4*3*0,5=72. |
||||||||
Ответ: 72кв.ед.
Пример3.
Дано: = − − + ; = + − ; = + + .
1)Построить ортонормированный базис.
2) Разложить вектор = − в этом базисе.
Решение:
1) = -2 +(-4)*2+1*(-3)=0 -2 =11 =-5,5
= {-2;-4;1}; = √
= {-11;2;-3}; = √
20