векторная алгебра

(; ; )- ортогональный базис. Для нахождения ортонормированного

базиса найдём соответствующие орты.

=√ {10;-17;-48}=

В естественном базисе координаты данного вектора: = {2;-5;0}

Для нахождения координат вектора в ортонормированном базисе используем формулы:

Ответ: = √ + √ +√

21

§5 Смешанное произведение.

Пусть дана тройка векторов ; ; .

Если сначала найти векторное произведение а× , а затем полученный вектор скалярно умножить на третий вектор с, то мы получим число,

которое обозначают ( ; ; ) и называют смешанным произведением векторов ; ; .

Определение: Смешанным произведением векторов ; ; называется

число полученное по правилу:

(;; )=( × )

Свойства смешанного произведения.

b

2.( ; ; )>0 ; ; правая тройка

3.(; ; ) 0 ; ; левя тройка

4.(; ; )=0 ; ; . вектора компланарны.

5.Смешанное произведение трёх некомпланарных векторов ; ; по

модулю равно объёму Vпараллелепипеда, построенного на данных векторах, как на рёбрах:

; ; =V

Вычисление смешанного произведения через координаты вектора.

= + + ; = + + ; =x3 +y3 +z3 .

× =(y1z2-z1y2) +(x1y2-y1x2) +(z1x2-x1z2)

(; ; ) = ((y1z2-z1y2)x3 +(x1y2-y1x2)y3 +(z1x2-x1z2)z3=

22

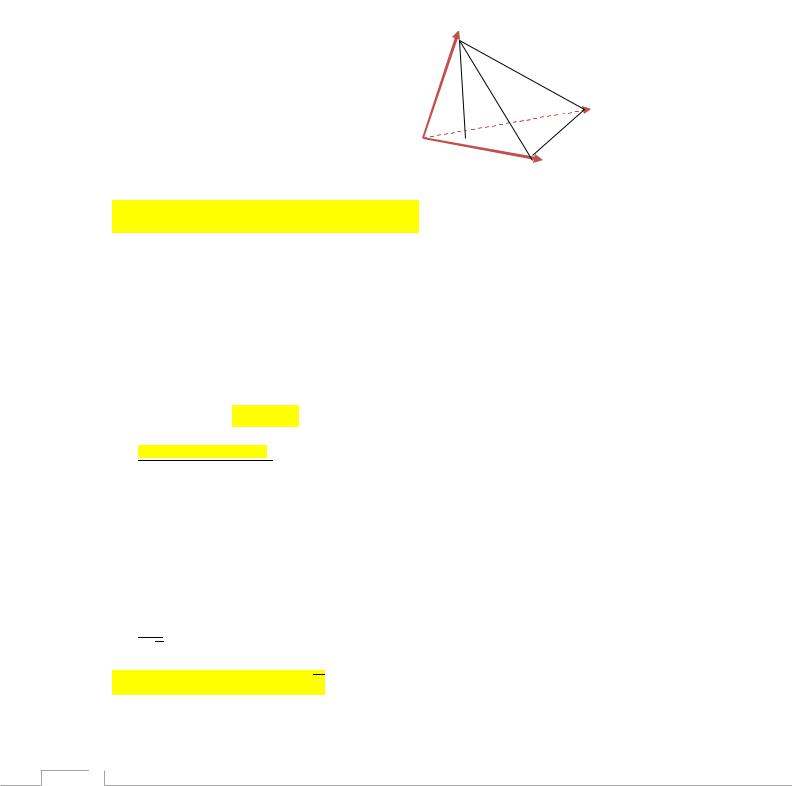
Пример:

Дан тетраэдр, вершинами которого являются точки А(1;-1;2);

В(2;1;2);С(1;1;4); D(6;-3;8).

Найти объём тетраэдра и длину высоты H, опущенной из вершины D на грань АВС.

Решение:

D

C

H

А

В

V(тетраэдра)=V(параллелелпипеда)

Найдём смешанное произведение векторов:

АВ={1;2;0}; ={0;2;2}; ={5;-2;6}

H= √ =3√

Ответ:V=6куб.ед; H=3√

23

Лекция 2. (для тех, кто хочет знать больше)

§6.Понятие об «n» мерном пространстве Rn.

П01 Определение:

Обозначим Rn множество, элементы которого (векторы), заданы в виде:

=(a1;a2;…;an)Т ai R; i=1;2;…;n

В эом множестве введён нулевой элемент:

=(0;0;…;0)

В этом множестве введены линейные операции.

1)Сложение:

Для любых векторов =(a1;a2;…;an)Т и =(b1;b2;…;bn)T ; ; Rn

однозначно определён вектор, называемый суммой векторов, по следующему правилу:

2)Умножение вектора на скаляр.

Для любого вектора а (а Rn) и числа R однозначно определён вектор,

обозначаемый а, по правилу:

=( a1; a2;…; an)T

Свойства сложения.

1) Свойство коммутативности.

a +0 = 0 +a для любого а

4)Существование противоположного вектора:

24

для любого а существует противоположный вектор, который

обозначают -а: +(− ) = − + = .

5)Свойство обратимости:

Для любых векторов и существует вектор : + = .

Вектор называется разностью и обозначается: = −

( = +(−)

Свойства умножения вектора на скаляр.

1) *( а) = ( )а

2)( + ) = +

3)1 =

4)-1 = −

5)0 =

Пространство Rn в этом случае называют линейным пространством, а его элементы векторами.

П02. Линейно зависимые и независимые системы векторов. Определение:

Система векторов а; а;…;а называется линейно зависимой, если

найдутся числа: 1; 2;…; n (не все равные нулю):

1 + 2 +…+ n =∑ = (линейная комбинация векторов равна

нулевому вектору при условии, что не все числа i равны нулю).

Если ∑ = тогда и только тогда, когда все числа i=0, i=1,2,…,n, то

система векторов а; а;…;а называется линейно независимой.

Критерий линейной независимости.

= .. ; = .. ;…; = ..

25

Рассмотрим матрицу , составленную из координат этих векторов:

По определению линейной независимости можно составить матричное уравнение:

имеет единственное нулевое решение , если ранг матрицы А равен числу неизвестных, т.е. r(A)=n.

Система векторов = .. ; = .. ;…; = ..

линейно независима r(A)=n

Замечание:

Если m=n, то однородная система имеет единственное нулевое

Решение:

Составим матрицу координат и определим её ранг, приведя её к

ступенчатому виду.

-2

−

А= − − ~ − − − ~ − −

26

r(A)=2; n=3 r(A)≠n система имеет ненулевые решения, т. е.

система векторов линейно зависима

Пример 2.

Такой пример будет в тесте!

Решение:

Вычислим определитель матрицы координат:

−

= − =0+4+15-(0-20+1)=38≠0 система векторов

линейно независима.

П04.Базис в пространстве Rn. Разложение вектора в этом базисе.

Определение:

Размерность линейного векторного пространства обозначается dim Rn. (Размерность равна «n», что определяет число координат в задании вектора).

два условия: 1)вектора линейно независимы, 2) dim Rn=n

Предложение:

Любой вектор Rn однозначно может быть разложен в этом

базисе, т.е. представляется линейной комбинацией базисных векторов:

Числа x1;x2;…;xn называют координатами вектора а в этом базисе.

27

Для нахождения координат вектора в заданном базисе необходимо решить систему:

…………………………………………….

+ + + =

Пример 3.

Используя результат примера 2, разложить вектор в этом базисе.

= −

−

28

П04. Скалярное произведение в пространстве Rn. Определение:

Скалярным произведением векторов =(a1;a2;…;an)Т и

=(b1;b2;…;bn)T ; ; Rn называется число, полученное по формуле:

(; )=a1*b1+a2*b2+…+anbn

Свойства скалярного произведения.

1.(; ) = ( ; )

2.( ; ) = (; )

3. (; + ) = ; +(; ) 4. (; )

Длина вектора определяется по формуле:

а = (а;а)= а +а + а

Замечание.

Линейное пространство называется евклидовым, если введено скалярное произведение. Таким образом, пространство Rn

является евклидовым «n» мерным векторным пространством.

Неравенство Коши-Буняковского.

Модуль скалярного произведения двух векторов не превышает произведения их длин.

Следствие:

(; ) ≤ 1

Ещё одна формула для вычисления скалярного произведения, которой мы уже раньше пользовались:

29

Определение:

Будем говорить, что два вектора и ортогональны, и записывать

тогда и только тогда, когда их скалярное произведение равно

нулю.

(; )=0

Определение ортонормированного базиса.

Базис , составленный из системы векторов

; ;…; называется ортонормированным, если вектора

попарно ортогональны и длины их равны 1.

Важное свойство ортонормированного базиса:

В ортонормированном базисе координаты любого вектора

а=( ; ;…; ) ,будут находиться по формулам Фурье, а именно:

=x1 +x2 +…+xn ,

1=( ; ) ; x2=( ; ); …; xn=( ; )

Это интересно!

Рассмотрим систему векторов: ;;…; , где

=(1,0,…,0)T; =(0,1,0,…,0)T; … ; =(0,0,…,0,1).

Проверим, что эти вектора образуют ортонормированный базис.

30