
- •Глава 1. Алгебра случайных событий
- •§1. Основные определения и понятия
- •Свойства противоположного события
- •2 Решение типовых задач
- •§3 Задачи для самостоятельного решения.
- •1) Построить пространство элементарных исходов
- •2) Указать состав подмножеств, соответствующих данным событиям
- •3) Выполнить указанные операции над данными событиями.
- •Глава 2 Классическое вероятностное пространство.
- •§1. Основные понятия и определения.
- •2) Все элементарные исходы равновозможные, т.Е.
- •Элементы комбинаторики.
- •§2. Решение типовых задач.
- •20 Футбольных команд, среди которых 4 призёра предыдущего первенства, по жеребьевке разбиваются на 4 занумерованные подгруппы по 5 команд.
- •Решение:
- •52 Карты раздаются четырём игрокам (каждому по 13 карт)
- •Решение:
- •4) Картошки, 5) наполеон, 6) невские.
- •Решение:
- •§3 Задачи для самостоятельного решения.
- •Глава 3 Относительная частота и её свойства
- •§1. Основные понятия.
- •Относительная частота события а:
- •4) Свойство устойчивости:
- •§2. Решение типовых задач
- •§3. Задачи для самостоятельного решения
- •Глава 4. Теоремы сложения и умножения вероятностей. Условная вероятность.
- •§1. Основные понятия
- •5)Теорема сложения для совместных событий:
- •6)Теорема умножения
- •7)Теорема о сумме совместных, но независимых в совокупности событий.
- •§2 Решение типовых задач.
- •Задача №6
- •Решение:
- •Глава 5. Формула полной вероятности. Формулы Байеса.
- •§1. Основные понятия
- •§2. Решение типовых задач. Задача 1
- •Задача 2
- •Задача 3
- •Задача 4.
- •Решение.:
- •Задача 5.
- •Решение:
- •Задача 6.
- •Решение.
- •Задача 8
- •Задача 9
- •§ 3 Задачи для самостоятельного решения
- •Задача 6.
- •Задача 7.
- •Задача 9.(новогодний аттракцион)
- •Задача 10.
- •Задача 11.
- •Задача 12.
- •Задача 13.
- •Задача 14.
- •Глава 6 Последовательность независимых испытаний
- •§1.Основные понятия
- •§2 Решение типовых задач
- •§3 Задачи для самостоятельного решения.
- •Задача 2.
- •Задача 3.
- •Глава 7. Одномерная случайная величина дискретного типа
- •1 Основные понятия
- •Полигон распределения
- •Основные дискретные распределения и их числовые характеристики
- •Задача2
- •Задача 3
- •Задача 7
- •Задача 8
- •Глава 8 Одномерная случайная величина непрерывного типа
- •§1 Основные понятия.
- •§2 Решение типовых задач
- •Задача 2
- •1)Основное свойство функции плотности:
- •Задача 3
- •Решение:
- •1)Основное свойство функции плотности:
- •Задача 4
- •Решение:
- •Задача5
- •Задача 6
- •§3 Задачи для самостоятельного решения
- •Задача 22
- •Задача 23
- •1. Строим график
- •§2 Решение типовых задач
- •§3. Задачи для самостоятельного решения
- •Глава 11. Непрерывная двумерная случайная величин
- •Условные математические ожидания
- •§ 2 Решение типовых задач
- •§ 3 Задачи для самостоятельного решения
- •Глава 12. Закон больших чисел (предельные теоремы)
- •§ 1. Основные понятия и формулы
- •1. Неравенство Маркова
- •2. Неравенство Чебышева
- •3. Неравенство Бернулли
- •§ 2. Решение типовых задач
- •§ 3. Задачи для самостоятельного решения
- •Глава 12. Нормальная случайная величина
- •§ 1. Основные понятия и формулы
- •§ 2. Решение типовых задач
- •§ 3. Задачи для самостоятельного решения
Глава 8 Одномерная случайная величина непрерывного типа
§1 Основные понятия.
Если множество значений случайной величины Х есть некоторый интервал или объединение интервалов числовой оси, то говорят о непрерывной случайной величине.
Непрерывная случайная величина задается с помощью функции f(x), которая называется плотностью распределения вероятности. При этом:
1)f(x)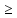 0
2)p
0
2)p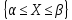 =
=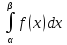
Замечание:
p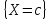 =
= =0
=0
Т.е. вероятность того, что значения непрерывной случайной величины попали в точку X=C, равна 0.
Основное
свойство функции плотности
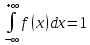
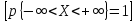
Функция распределения непрерывной случайной величины
F(x)=P{X<x}=
P{-∞<X<x}=
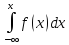
Функция распределения непрерывной случайной величины является первообразной для функции плотности f(x), т.е.
F`(x)=f(x)
Заметим,
что p{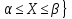 =
=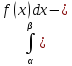 вероятность попадания в интервал
численно равна площади криволинейной
трапеции под кривойf(x).
вероятность попадания в интервал
численно равна площади криволинейной
трапеции под кривойf(x).
Часто функцию f(x) называют дифференциальным, а функцию распределения F(x) интегральным законами распределения непрерывной случайной величины.
Основные свойства функции распределения F(x) непрерывной случайной величины.
1.Область определения
D(F)=(-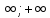 )
)
2.Множество значений
E(F)=[0;1]
или (0;1), при этом
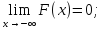
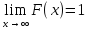
3.Монотонность:
Неубывающая:
т.е. если x1>x2,
F(x1)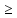 F(x2)
[нет точек extr]
F(x2)
[нет точек extr]
4.Непрерывная функция
5.Для вычисления вероятности попадания в интервал справедливы следующие формулы:
P{X< }
=F(
}
=F(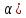
P{X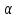 }
= 1 - F(
}
= 1 - F(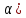
P{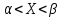 }
=P{
}
=P{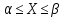 }
=P{
}
=P{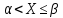 }
=P{
}
=P{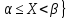 =F(
=F(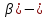 F(
F(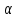 )
)
Типовые графики:
f(x)
.
x
a
b
F(x)
a
1
b
x
S=1
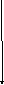


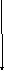








F(a)=0
F(b)=1
1
f(x)
F(x)
1


S=1


2.

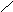

x
x

a
a
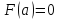
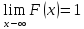
F(x)
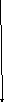
f(x)



S=1
1
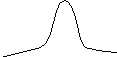
3
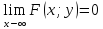
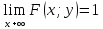



х


m
m
x
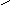


Числовые характеристики непрерывной случайной величины (формулы для вычисления)
M[X]=
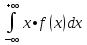 [математическое
ожидание][предполагается,
что
[математическое
ожидание][предполагается,
что
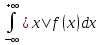 сходится]
сходится]
Если это требование не выполнено, то с.в. Х [не имеет математического ожидания]
D[X]=M[(X-mx)2] [дисперсия]
D[X]=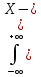 mx)2•f(x)dx
mx)2•f(x)dx
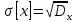 -среднее
квадратическое отклонение
-среднее
квадратическое отклонение
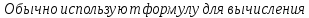 :
:
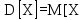 -2]
– (mx)2=
-2]
– (mx)2=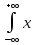 2•f(x)dx
– (mx)2
2•f(x)dx
– (mx)2
Начальные моменты «кго» порядка
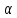 к=M[Xк]=
к=M[Xк]=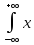 к•f(x)dx
к•f(x)dx
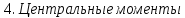 «кго»
порядка
«кго»
порядка
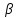 к=M[(X-mX)к]=
к=M[(X-mX)к]=
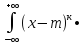 f(x)dx
f(x)dx
Замечание:
Свойства математического ожидания и дисперсии рассмотренные в главе 6 для дискретной случайной величины, справедливы для непрерывной случайной величины.
Основные непрерывные распределения
Равномерное распределение на отрезке.R[a;b]
Случайная величина Х называется равномерно распределённой на отрезке [a;b], если её функция плотности задаётся формулой
f(x)=
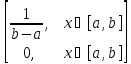 F(x)=
F(x)=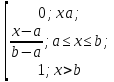 функция
распределения
функция
распределения
F(x)
1
M[X]=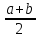 ;D[X]=
;D[X]=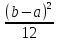 ;X=
;X=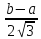

f(x)






x


a
b
a
b
x
Замечание: Равномерное распределение на отрезке [0;1] является стандартным. Существуют таблицы случайных чисел, распределённых равномерно на [0;1]. Стандартное распределение R[0,1] заложено в компьютерах, микрокалькуляторах, которые по специальным программам производят псевдослучайные числа, распределённые на [0;1]. Имеются формулы, программы, преобразующие равномерный закон распределения в другие законы.
Показательное распределение с параметром а
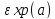
X
распределена
по показательному закону с параметром
а, если функция
плотности
задаётся формулой: f(x)=
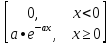
f(x)
a

x
Функция распределения:
F(x)=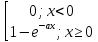
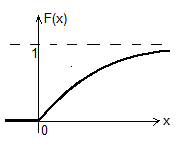
M[χ]=1/a; D[χ]=1/a2; σx=1/a
3)
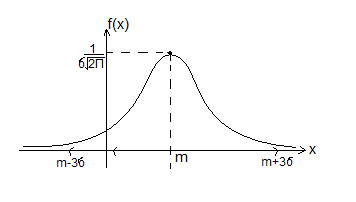
Нормальное распределение (закон Гаусса)
с параметрами m,
σ
(обозначается:
N (m, σ) M[χ]=m; D[χ]= σ2
Случайная
величина χ распределена нормально с
параметрами m,
σ, если функция плотности задается
формулой![]()
![]()
f(x)=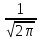 *
*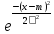
Если
m=0,
σ=1,
то имеем стандартизированную случайную
величину. Функция
плотности: (x)=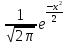
![]()
[есть таблица значений этой функции]
1


F(x)
Функция
распределения
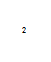
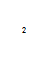
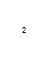
![]()


1/2
F(x)=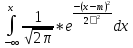
m

X
Чтобы
найти значения функции распределения
используют таблицу значений функции
Лапласа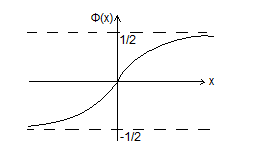
Ф(x)=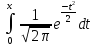
Ф(-x)=-
Ф(x)![]()
Ф(х)=1/2
F(x)=0,5+Ф((x-m)/σ)
Основные формулы для вычисления вероятностей попадания в интервалы
1. Р{χ<α}=0,5+Ф((α-m)/σ)
2. P{χ>β}=0,5- Ф((β-m)/σ)
3. P{α<χ<β}=Ф((β-m)/σ)-Ф((α-m)/σ)
4. P{|χ-mx|<ε}=2Ф(ε/σ)
5. P{|χ-mx|<kσ}=2Ф(k)
В частности: Правило “3σ”: P{|χ-mx|<3σ}=2Ф(3)=0,9973
Замечание: Во многих задача инженерной практики считают допустимым пренебрегать вероятностями меньше, чем 1-0,9973=0,0027≈0,003
