Полигон распределения

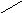
x

X₁

_X2

X_i

X_n

• Определение Функцией распределения случайной величины Х называется числовая функция , которую обозначают F( х ), равную вероятности события { X x ),т.е.

• F ( х )=P { X  x }.

Функция распределения вычисляет вероятность попадания слева

от точки х.

Для дискретной случайной величины функция распределения задаётся следующей формулой:

F( х ) ==

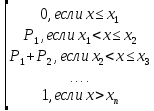
F(x)

1

x

x₁

x_i

x_n

Свойства функции распределения

1. Область определения: D( F )=(-∞; +∞ ).

2. Множество значений : E(F )= [ 0, 1].

3. Монотонность : F( х )- неубывающая функции ,т.е.

если х ₁х₂ ,то F ( х₁₎ ≤F( х₂)

4. Непрерывность : В точка х_i – функция имеет разрыв справа  рода, при этом F (х_{i +}0) –F ( x_i- 0) =p_i ( предел справа минус предел слева равен p_i= P{ X =x_i})

Числовые характеристики

( формулы для вычисления числовых характеристик дискретной случайной величины )

1Математическое ожидание определяет средне статистическое значение случайной величины или центр распределения вычисляют по формуле: m_x=M[ X ] = ∑ х_i*p_i ( В случае бесконечного числа значений случайной величины числовой ряд должен сходится ).

1. Дисперсия случайной величины ( определяет меру рассеяния относительно центра распределения ) вычисляется по формуле:

D [Х] =M[ ( X – m_x)²] D[ X ]=∑ ( х_i – m_x )²*p_i

3 Среднее квадратичное отклонениеaa

• _х =[ x] =

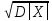
4Начальные моменты «к» го порядка

_к =М[ X ^k ]=∑х_i^k _*p_i ₁= M[X ].

5 Центральные моменты «к» го порядка

_к =M[(Х –m_x)^k] ,₁=0, ₂= D[x]

• 

1. M[C] =С, ( С- константа)

2. М[  X+ C] =M[X] + C

3. M[X +Y+C] =M[x] +M[Y] +C, (Х., Y-случайные величины; , - числа; С – константа)

4. Если X и Y независимые случайные величины, т е.для любых х,y верно: P{(Xx)(Yy)}=P{Xx}P{Yy}. то M[XY]=M[X]*M[Y]

5. Если Y=(X) (Y функция случайной величины X),то M[Y]=∑(х_i)*P_i

Замечание Используя свойства математического ожидания, можно получить формулу для вычисления D[X]=M[(X- m_x)²]=

=M[X²- 2*m_x*X +(m_x)²]=M[X²]-2*m_x*M[X] + (m_x)² =M[X²]-(m_x)²

D[X] =M[X²] –( mx)² Заметим: ∑ х_i²p_i= M[X²]

Свойства дисперсии средне квадратичного отклонения

D[C]=0	[C]=0
D[kX+c]=k2D[X]	[kX+c]=к[X]
Если XиYнезависимые случайные величины, То:D[k1X+ k2Y+ C ]=k12D[X] +k22D[Y]	Если XиYнезависимые случайные величины, То: [k1X +k2Y +C] = k1[X]+k2[Y]

Основные дискретные распределения и их числовые характеристики

1 Индикатор U события A

U	0	1
P	P	q

р(А) =p, p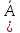)=q

M[U]=p, D[U] = p*q.

2 Биномиальное распределение

Х –число появлений события А в «n» независимых испытаниях Бернулли

P{X=k}= P_n(к)=C_n^kp^k*q^n-k, к=0,1,…,n

X	0	1	2	…	k	…	n
P	qn	nqn-1p	Cn2 qn-2 p2	…	Cnkpkqn-k	…	pn

(Коэффициенты C_n^k можно легко получить, используя треугольник Паскаля, см. глава 2)

M[X]= n*p, D[X]=npq, [X]=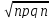

3 Распределение Пуассона

Случайная величина Х распределена по закону Пуассона с параметром , если P_k=P{X=k}=()^k/k!*e^-, к=0,1,2,…,n,…

Т.к. имеем счётное множество значений, то числовой ряд ∑p_к =1(числовой ряд сходится и сумма ряда равна 1)

X	0	1	2	3	…	К	…
P	e-	e-	2/2 *e-	3/6*e-	…	k/k!*e-	…

M[X]=,…….D[X]=,…..[X]=

Замечание Распределение Пуассона является предельным для биномиального:

Pn(k)^k/k!*e^- n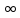,где =n*p

4 Геометрическое распределение

Пусть в одном опыте событие А появляется с вероятностью р ,т. е. Р(А)=р, Р(А)= 1-р=q

Опыты проводятся до первого появления события А.

Х –число опытов. р_к=Р{X=k}=q^k-1p, к=1,.2,.3.,…,n,…

Заметим, что выполнено условие: ∑р_к=1 ( числовой ряд сходится и его сумма равна 1 )

Х	1	2	3	…	К	…
Р	Р	qp	q2p	…	qk-1p	…

М[X]=1/p, D[X]=q/p², [X]=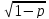/q

5.Гипергеометрическое распределение

• В урне а белых и в чёрных шаров.Из урны вынимают n шаров. Пусть Х- число белых шаров, среди вынутых шаров.

Р_к=Р{X=k}=C_a^k C_В^n-k/C_а+вⁿ , к=0, 1, 2, …., а

Х	0	1	….	К	…	а
Р	Свn/Са+вn	Р1	…	Рк	…	Свn-a/Cа+вn

M[X]=na/a+в.

§2 Решение типовых задач

Задача 1

Пусть случайная величина Х задана рядом распределения:

Х	-3	-2	0	1	2
Р	0.1	0.2	0.3	0.1	0.3

1. Построить полигон распределения.

2. Найти функцию распределения F(x).

3. Найти следующие вероятности: P{X1},P{-2≤X≤2}.

4. Математические ожидания: M[X],M[4X-1].

5. Найти дисперсии: D[X],D[-3X+5]

0,3

Решение

0.2

1)

0,1

-3

-2

1

2

2) F(x)=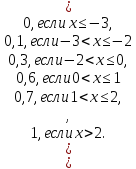

График функции распределения

1

1

1111

F(x)

х

-3

0

1

2

-2

3)Р{X1}=1-P{X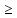1}=1-(P{X=1} +P{X=2})=1-0,1-0,3=0,6, P{-2≤X≤2}=1-P{X=-3}=1-0,1=0,9.

4)M[X]=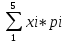=-3*0,1-2*0,2+0*0,3+1*0,1+2*0,3=0

М[4*X-1]=4 M[X]-1=-1

5)D[X]=M[X²]-(m_x)², M[X²]=∑x_i² p_i=9 *0,1+4*0,2+0*0,3 +1*0,1+4*0,3=3

D[X]=3-0²=3 , D[-3X+5]=9*D[X]=3*9=27.

Задача 2

Два мальчика бросают мяч в кольцо, но не более двух раз каждый. По жребию начинает первый. Если один попадает, то игра заканчивается.

Пусть А₁={попал первый}; Р(А₁)=0,8

А₂={попал второй}; Р(А₂) =0,6

(события А₁ и А₂ –независимые).

Х–число бросков, Х{1, 2, 3, 4}

1) Составить ряд распределения.

2)Найти функцию распределения F(x)’.

3)Найти вероятность :Р{X3}.

4) М[X]- среднее число бросков.

Решение

1)Составление ряда распределения

р₁=Р{X=1} =P(A₁)=0,8

p₂=P{X=2}=P(A⁻₁ A₂)=P(⁻A₁)*P(A₂)=0,2*0.6 = 0,12.

р₃=P{X=3}=P(A⁻₁*A⁻₂*A₁)=Р(А⁻₁)*Р(А⁻₂)*Р(А₁)=0,2*0.4*0.8=0.064

p₃=P{X=4}=P(A⁻₁*A⁻₂*A⁻₁)=р(А⁻₁)*р(А⁻₂)*р(А⁻₁)=0.2*0.2*0.4=0.016.

Х	1	2	3	4
Р	0.8	0.12	0.064	0.016

Контроль:р₁+р₂+р₃+р₄= 1

4)Среднее число бросков

М[X]=∑х_ip_i=1*0.8+2*0.12+3*0.064+4*0,016=1.296

(Задания 2) и 3) сделайте самостоятельно ).

Задача 3

Студент сдаёт экзамен по математике с вероятностью 0,4 .Студенту разрешили сдавать экзамен не более 4^х раз.

Пусть A={Студент сдал экзамен}, Р(А)=0,4.

Х-число попыток сдать экзамен.

1. Составить ряд распределения.

2. Найти математическое ожидание М[X].

3. Найти вероятность события: P{X-m_x k*} , где к=1,2,3,; -с.к.о.

Решение

1. Составление ряда распределения:р₁= р{X=1}=р(А)=0.4 ,р₂=p{X=2}=р(А⁻*А)=0,6*0,4=0,24; р₃=р{X=3}=р(А⁻*А⁻*А)=0,6*0,6*0,4=0,144.; р₄=р{X=4}=р(А⁻*А⁻*А⁻)=0.6*0,6*0,6=0,216.

Х	1	2	3	4
Р	0,4	0,24	0,144	0,216

Контроль: р₁+р₂+р₃+р₄=1

2. М[x]=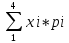=1*0,4+2*0,24+3*0.144+4*0,216=2,176

3. Для нахождения _х, найдём сначала дисперсию D[X].Для этого используем формулу:D[X]=M[X²]-(m_x)². M[X²]=∑x_i²*p_i=1*0,4+4*0,24+9*0,144+16*0,216=6,112

D[X]=6,112-(2,176)²= 1,377024 _х=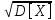=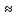1,17

К=1 P{X-2,1761,17}=Р{1,006Х3,346}= Р{X=1}+P{X=2}+P{X=3}=1-P{X=4}=1-0,216=0,784.

к=2 P{X-2,1762,34}=P{-0,164Х4,516}=1 (2*=2,34)

к=3 P{X-2,1763*} =1

Задача 4

Дано: Случайная величина Х задана рядом распределения, при этом М[X]=3,1.

Х	-2	0	3	В
Р	0,1	0,2	а	0,4

Найти:1)а;2)в;3) функцию распределения F(x)

Решение:

1. а=1-(0,1+0,2+0,4)=0,3

2. М[X]==3,1=-2*0,1+0*0,2+3*а+в*0,4в=0.4

3)F(x)=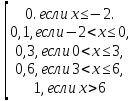

Задача 5

Дано: F(x)=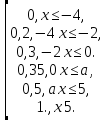

М[X]=1,95

1)Составить ряд распределения

2)Найти параметр а .

Решение:

Х	-4	-2	0	а	5
Р	0,2	0,1	0,5	0,15	0,5

M[X]=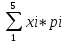=1,95

-4*0,2+(-2)*0,1+0*0,5+а*0,15+5*0.5=1,95а=3

Задача 6

Дано:

Х	-4	В	0	а
Р	0,2	0.5	0,1	0,2

Найти:1) а; 2) в.

Решение

Область допустимых значений для параметров :-4в0а

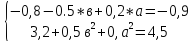
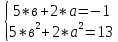
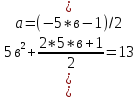
35в²+10в-25=07в²+2в -5=0в₁=-1, в₂=5/7 (посторонний корень)

Ответ: а=2; в=-1

Задача 7(Биномиальное распределение)

В пяти ВУЗах случайным образом отобрали по одному студенту для проведения тестирования на употребление наркотиков. По статистике , вероятность того, что студент ВУЗа употребляет наркотики равна 0,4.

Пусть А={студент является наркоманом}.Р(А)=0,4=р, q=0,6.

Х- число наркоманов.

1. Составить ряд распределения Х.

2. Математическое ожидание M[X]/

3. Дисперсию D[X].

4. Вероятность P{X-m_x}

Решение

1)

Х	0	1	2	3	4	5
Р	q5	5pq4	10p2q3	10p3q2	5p4q	P5
P	0,07776	0.2592	0,3456	0.2304	0,0768	0.01024

2)M[X]=n*p=5*0,4=2

3)D[X]=npq= 2*0,6=1,2. _х==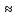1,1.

4)P{X-2 1,1}=P{0,9Х3,1}=P{X=1}+P{X=2}+P{X=3}=0,8352.

Задача 8 (гипергеометрическое распределение)

В группе студентов 4 девушки и 3 юноши являются претендентами для поездки в Германию. Случайным образом выбирают трёх человек.

Х –ЧИСЛО ДЕВУШЕК В «ТРОЙКЕ»

1. Составить ряд распределения для Х.

2. Математическое ожидание M[X]

3. Дисперсию D[X]

4. Вероятность P{X3}

Решение

1. =12/35;P₃=P{X=2}=(C₄²*C₃¹)/C₇³ =6*3/35= 18/35;P{X=3}= С₄³/С₇³=4/35.

Х	0	1	2	3
Р	1/35	12/35	18/35	4/35

Контроль:р₁+р₂+р₃+р₄=1

2)M[X]=12/35+36/35+12/35=60/35=12/7.

3)D[X]=M[X²]-(m_x)².

M[X²]=12/35+72/35+36/35=120/35;D[X]=120/35-(12/7)²=24/49. _х

4)P{X3}=P{X2,1}=1-P{X=3}=1-4/35=31/35

Задача 9(Распределение Пуассона)

Х-число просроченных товаров на складе распределено по закону Пуассона с параметром =2.

1. Построить ряд распределения Х.

2. Найти вероятность P{X2}/

3. Математическое ожидание :M[5-3*X].

4. Дисперсию D[6-0,1*Х].

5. Вероятность:P{X-m_x2}

Решение

Х	0	1	2	3	…	К
Р	e-2	2*e-2	4/2*e-2	8/6*e-2	…	k/k!*e-
P	0,135	0.271	0,271	0.18	…	…

2)P{X2}=1-P{X=0}-P{X=1}=0,594.

3)M[X]==2; M[5-3*X]=5-3*M[X]=5-3*2=-1

4)D[X]=; D[6-0.1*X]=0,01D[X]=0,02

5)_х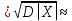1,4; 2*_х=2,8

P{X-22.8}=P{-0,8Х3,4}=P{X=0}+P{X=1}+P{X=2}+P{X=3}=0.947

Задача 10 (Геометрическое распределение)

Упорный футболист пытается забить гол в ворота .В среднем он поражает ворота с вероятностью 0.1.Футболист решил бить по воротам до тех пор пока не попадёт.

Пусть А={попадание в ворота},Р(А)=0,1.

Х- число попыток забить гол (р=0.1, q=0.9)

1. Составить ряд распределения.

2. Найти математическое ожидание:M[X]/

3. Найти дисперсию: D[3-2*X].

4. Найти вероятность:P{X3}

Решение

1)

Х	1	2	3	4	…	К
Р	Р	P*q	q2*p	q3*p	…	qk-1*p
P	0,1	0.09	0.081	0.0729	…	…

2)M[X]=1/p=10.

3)D[X]=q/p²=0,9/0.01=90. D[3-2*X]=4*D[X]=360.

4) P{X3}=1-P{X=1}-P{X=2}=1-0,1-0,09=0,81.

§

Задача 1

Число телефонных звонков, поступивших в справочное бюро от абонентов между полуднем и часом дня в любой день недели, есть случайная величина Х, заданная таблицей:

Х	0	1	2	3	4	5
Р	0.3	0,2	0,2	0,1	0,1	0.1

1. Убедитесь, что задан ряд распределения.

2. Найти функцию распределения F (х) и построить график.

3. Используя функцию распределения F(х), определите вероятность того, что между 12 час.34 мин. и 12 час. 35 мин. в справочное бюро поступит больше двух звонков

4. Математическое ожидание .M[X].

5. Дисперсию D[X].

Ответ:a) =1 ; с)P[X>2}=1-F(2)-P{X=2}=0,3;d)M[X]=1,8; e) D[X]=2,66.