
- •Глава 1. Алгебра случайных событий
- •§1. Основные определения и понятия
- •Свойства противоположного события
- •2 Решение типовых задач
- •§3 Задачи для самостоятельного решения.
- •1) Построить пространство элементарных исходов
- •2) Указать состав подмножеств, соответствующих данным событиям
- •3) Выполнить указанные операции над данными событиями.
- •Глава 2 Классическое вероятностное пространство.
- •§1. Основные понятия и определения.
- •2) Все элементарные исходы равновозможные, т.Е.
- •Элементы комбинаторики.
- •§2. Решение типовых задач.
- •20 Футбольных команд, среди которых 4 призёра предыдущего первенства, по жеребьевке разбиваются на 4 занумерованные подгруппы по 5 команд.
- •Решение:
- •52 Карты раздаются четырём игрокам (каждому по 13 карт)
- •Решение:
- •4) Картошки, 5) наполеон, 6) невские.
- •Решение:
- •§3 Задачи для самостоятельного решения.
- •Глава 3 Относительная частота и её свойства
- •§1. Основные понятия.
- •Относительная частота события а:
- •4) Свойство устойчивости:
- •§2. Решение типовых задач
- •§3. Задачи для самостоятельного решения
- •Глава 4. Теоремы сложения и умножения вероятностей. Условная вероятность.
- •§1. Основные понятия
- •5)Теорема сложения для совместных событий:
- •6)Теорема умножения
- •7)Теорема о сумме совместных, но независимых в совокупности событий.
- •§2 Решение типовых задач.
- •Задача №6
- •Решение:
- •Глава 5. Формула полной вероятности. Формулы Байеса.
- •§1. Основные понятия
- •§2. Решение типовых задач. Задача 1
- •Задача 2
- •Задача 3
- •Задача 4.
- •Решение.:
- •Задача 5.
- •Решение:
- •Задача 6.
- •Решение.
- •Задача 8
- •Задача 9
- •§ 3 Задачи для самостоятельного решения
- •Задача 6.
- •Задача 7.
- •Задача 9.(новогодний аттракцион)
- •Задача 10.
- •Задача 11.
- •Задача 12.
- •Задача 13.
- •Задача 14.
- •Глава 6 Последовательность независимых испытаний
- •§1.Основные понятия
- •§2 Решение типовых задач
- •§3 Задачи для самостоятельного решения.
- •Задача 2.
- •Задача 3.
- •Глава 7. Одномерная случайная величина дискретного типа
- •1 Основные понятия
- •Полигон распределения
- •Основные дискретные распределения и их числовые характеристики
- •Задача2
- •Задача 3
- •Задача 7
- •Задача 8
- •Глава 8 Одномерная случайная величина непрерывного типа
- •§1 Основные понятия.
- •§2 Решение типовых задач
- •Задача 2
- •1)Основное свойство функции плотности:
- •Задача 3
- •Решение:
- •1)Основное свойство функции плотности:
- •Задача 4
- •Решение:
- •Задача5
- •Задача 6
- •§3 Задачи для самостоятельного решения
- •Задача 22
- •Задача 23
- •1. Строим график
- •§2 Решение типовых задач
- •§3. Задачи для самостоятельного решения
- •Глава 11. Непрерывная двумерная случайная величин
- •Условные математические ожидания
- •§ 2 Решение типовых задач
- •§ 3 Задачи для самостоятельного решения
- •Глава 12. Закон больших чисел (предельные теоремы)
- •§ 1. Основные понятия и формулы
- •1. Неравенство Маркова
- •2. Неравенство Чебышева
- •3. Неравенство Бернулли
- •§ 2. Решение типовых задач
- •§ 3. Задачи для самостоятельного решения
- •Глава 12. Нормальная случайная величина
- •§ 1. Основные понятия и формулы
- •§ 2. Решение типовых задач
- •§ 3. Задачи для самостоятельного решения
Глава 11. Непрерывная двумерная случайная величин
§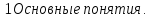
Если значения двумерной случайной величины (Х;У) заполняют некоторую область (D) на координатной плоскости (Х0У) и при этом известна неотрицательная функция двух аргументов f(x;y) – функция плотности распределения вероятности случайной величины (Х;У), такая что:
P{(X,Y)()}=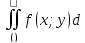 , где ()
–произвольная область координатной
плоскости, то
(Х;У)-непрерывная двумерная случайная
величина.
, где ()
–произвольная область координатной
плоскости, то
(Х;У)-непрерывная двумерная случайная
величина.
Свойства функции плотности
f(x;y)0, (x;y)R.2
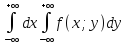 =1(основное
свойство ).
=1(основное
свойство ). a;b)}=0
(вероятность попасть в точку равна
нулю).
a;b)}=0
(вероятность попасть в точку равна
нулю).
Функция распределения непрерывной двумерной случайной величины
FXY(x;y)=P{(Xx)*(Yy)}=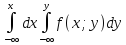 ,при этом: f(x;y)=
,при этом: f(x;y)=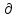 2F(x;y)/(∂x*∂y)
2F(x;y)/(∂x*∂y)
Cсвойства функции распределения
Область определения: (Х;У)R2 (все точки координатной плоскости)
Множество значений: 0≤F(x;y)≤1; при этом
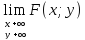 =1
=1
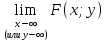 =0
=0Функция не убывает по каждому из аргументов, т.е.
если х1х2 и у1у2, ,то F(x1;y1) ≤ F(x2;y2)
Условия согласованности
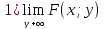 =Fx(x)
=Fx(x)
 =Fy(y)
=Fy(y)
2)fX(x)=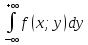 ;
fy(y)=
;
fy(y)=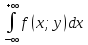
Независимые случайные величины
Х и У- независимые случайные величины, если независимы события:
A={Xx} и B={Yy} для всех значений х и у.
Необходимое и достаточное условие независимости
F(x;y)=Fx(x)*Fy(y)
fxy(x;y)=fx(x)*fy(y)
Числовые характеристики двумерной случайной величины
Центр распределения это точка М(mx;my), где
mx= fx(x)dx
fx(x)dx
my=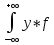 y(y)dy
y(y)dy
2)Корреляционный момент
K[X;Y]=M[(X-mx)*(Y-my)]
=
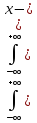 mx)*(y-my)*f(x;y)dx*dy
mx)*(y-my)*f(x;y)dx*dy
или по формуле: K[X;Y]=M[X*Y]-mx*my .где
M[X*Y]
=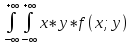 dxdy
dxdy
3)Коэффициент корреляции
R[X;Y]=xy=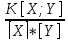 ;где
х=
;где
х=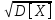 ;y=
;y=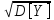
Заметим, что если K[X;Y]=0, то Х и У называются некоррелированными.
Условные законы распределения
Если (Х;У) непрерывная случайная величина, то условной плотностью распределения случайной величины Х при условии У=у
называется
:
f(x/y)=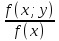 ;аналогично f(y/x)=
;аналогично f(y/x)=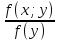
Условной функцией распределения случайной величины Х
при условии У=у называется :
Fx(x/y)=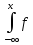 X(x/y)dx
аналогично: Fy(y/x)=
X(x/y)dx
аналогично: Fy(y/x)= y(y/x)dy
y(y/x)dy
Условные математические ожидания
Регрессия
У по Х
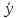 (х)=M[Y/X]=
(х)=M[Y/X]=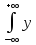 *fy(y/x)dy
*fy(y/x)dy
Регрессия
Х по У
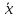 (y)=M[X/Y]=
(y)=M[X/Y]=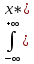 fx(x/y)dx
fx(x/y)dx
§ 2 Решение типовых задач
Задача 1.
Пусть (Х;У) –непрерывная случайная величина, распределённая равномерно в области (D)- прямоугольник на плоскости (см. рисунок)
у
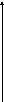
1
D








х
2
Зависимы или нет случайные величины Х и У?
Решение:
По определению, если случайная величина (Х;У) распределена равномерно в области (D), то функция плотности вычисляется по формуле:
f(x;y)=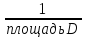 ,если (Х;У)(D).
,если (Х;У)(D).
В
нашем случае: f(x;y)=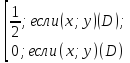
Рассмотрим условия согласованности:
fX(x)=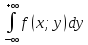 =
=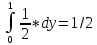 для всех х[0;2]
для всех х[0;2]
;
fy(y)= *dx=1
для всех у[0;1]
*dx=1
для всех у[0;1]
fx(x)*fy(y)=1/2*1=1/2=fxy(x;y) для всех значений х и у из области (D)
Вывод: Х и У –независимые случайные величины.
Задача 2
Пусть (Х;У) –непрерывная случайная величина, распределённая равномерно в области (D)- треугольник на плоскости (см. рисунок)
у
2
х
2
D




Найти линии регрессии.
Центр распределения M(mx;my).
Момент корреляции K[X;Y].
Решение:
Площадь
треугольника: S=2
fxy(x;y)=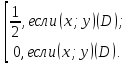
Условия согласованности:
fx(x)=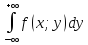
fx(x)=
fx(x)=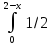 *dy
=1/2*(2-x),
если х[0;2].
*dy
=1/2*(2-x),
если х[0;2].
fy(y)=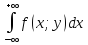
fy(y)=
fy(y)= *dx=1/2(2-y),
если у[0;2].
*dx=1/2(2-y),
если у[0;2].
Заметим,
что fx(x)*fy(y)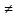 fxy(x;y)
Х и У зависимые случайные величины.
fxy(x;y)
Х и У зависимые случайные величины.
Рассмотрим условные функции плотности:
:
f(x/y)=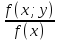 =
=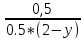 =
= ; если у[0;2];
x[0;2-y]
; если у[0;2];
x[0;2-y]
f(y/x)=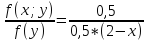 =
=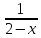 , если х[0;2];
y[0;
2-x]
, если х[0;2];
y[0;
2-x]
Регрессии:
Регрессия
У по Х
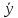 (х)=M[Y/X]=
(х)=M[Y/X]=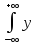 *fy(y/x)dy=
*fy(y/x)dy=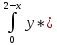 (1/(2-х)dy=
(1/(2-х)dy=
=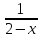 *y2/2
02-x=0,5*(2-x),
если х
[0;2]
*y2/2
02-x=0,5*(2-x),
если х
[0;2]
Регрессия
Х по У
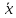 (y)=M[X/Y]=
(y)=M[X/Y]=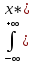 fx(x/y)dx=0,5*(2-y),
если у[0;2]
fx(x/y)dx=0,5*(2-y),
если у[0;2]
y
2
x
0
1
2
1
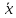 (y)
(y)
 (x
(x







2)M[X]=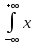 *f(x)dx=
*f(x)dx=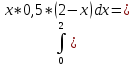 0,5*(x2-x3/3)02=2/3
0,5*(x2-x3/3)02=2/3
В силу симметрии M[Y]=2/3Центр распределения: M(2/3; 2/3)
3)Момент корреляции:
:
K[X;Y]=M[X*Y]-mx*my
.где M[X*Y]
=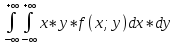
M[X*Y]=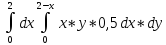 =
=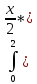 (0,5*y202-x)dx
=
(0,5*y202-x)dx
=
=1/4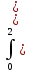 x3-4*x2+4*x)dx=1/4*(x4/4-
4/3*x3+4/2*x2)02=1/3
x3-4*x2+4*x)dx=1/4*(x4/4-
4/3*x3+4/2*x2)02=1/3
K[X;Y]=1/3-2/3*2/3=-1/9; K[X;Y]=-1/9
Задача 3
Пусть (Х;У) –непрерывная случайная величина, распределённая равномерно в области (D) -четверть круга на плоскости (см. рисунок)
x2+y2≤1; x0; y0
.Найти:
fxy(x;y) (двумерную функцию плотности)
Одномерные законы распределения: fx(x); fy(y).
Найти центр распределения М(mx;my)
Найти среднеквадратичные отклонения:x ;y.
Найти коэффициент корреляции ху.
Проверить, зависимы или нет случайные величины Х и У
Решение
У
y=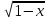 2
2
1



D
……
Х
1
0


Площадь D=
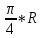 2=
2=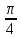
f(x;y)=
f(x;y)=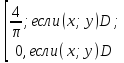
fX(x)=
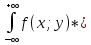 dy=
dy=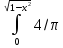 dy=4/π*
dy=4/π*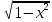 ,
x[0;1].
,
x[0;1].
f(x)=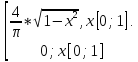
Аналогично:
f(y)=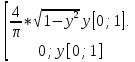
3)
mx=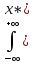 fx(x)dx
=
fx(x)dx
=
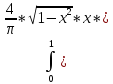 dx=-2/π
dx=-2/π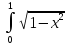 d(1-x2)=
d(1-x2)=
-2/π*2/3*(1-x2)3/201=4/3π.
Аналогично: my=4/3π
Таким образом: M(4/3; 4/3)
4)D[X]=M[X2]-mx2
M[X2]=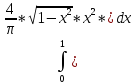
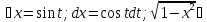 =
=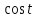 ;
x=0t=0;
x=1t=π/2]
;
x=0t=0;
x=1t=π/2]
4/π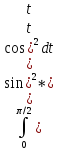 =1/π
=1/π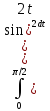 =
=
1/2π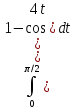 =1/2π(t-1/4*
=1/2π(t-1/4* 0π/2=1/2π(π/2-0)=1/4
0π/2=1/2π(π/2-0)=1/4
D[X]=1/4-(4/3π)2 0,069873
0,069873
x= x
x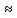 0,26
0,26
Аналогично:у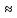 0,264
0,264
5):
K[X;Y]=M[X*Y]-mx*my
.где
M[X*Y] =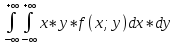
M[X*Y]=4/π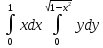 =4/π
=4/π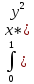 0
0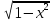 )dx=
)dx=
2/π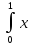 *(1-x2)dx=2/π(x2/2
–x4/4)01=2/π*(1/2-1/4)=1/2π≈0,1592
*(1-x2)dx=2/π(x2/2
–x4/4)01=2/π*(1/2-1/4)=1/2π≈0,1592
K[X;Y]=1/2π-(4/3π)2≈-0,02097
R[X;Y]=xy=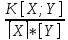 ≈
≈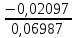 ≈-0,3
≈-0,3
6)Х
и У зависимы,
т.к. Кху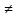 0
0
Задача 4
Плотность
вероятности двумерной случайной величины
(Х;У) задана формулой: fXY(x;y)=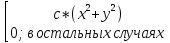 ;при
0≤х≤1;
0≤у≤1;
;при
0≤х≤1;
0≤у≤1;
Найти:
Коэффициент С
Одномерные функции плотности: fX(x); fY(y)
Центр распределения M(mX;my).
Cредне квадратичные отклонения Х и У.
Коэффициент корреляции ХУ.
Проверить, зависимы или нет случайные величины Х и У.
Решение
Изобразим на плоскости область определения функции f(x;y)
X
D
1
0






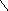
1
Y
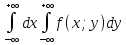 =1
-основное свойство функции плотности
=1
-основное свойство функции плотности
с*
 )dy
=c*(
)dy
=c*(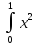 dx
dx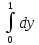 +
+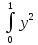 dy
dy )=
)=
=2*c(x3/301*1)=2/3*c2/3*c=1c=3/2
fX(x)=
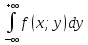 fX(x)=3/2
fX(x)=3/2 dy=3/2(x2*y+y3/3)01=
dy=3/2(x2*y+y3/3)01=
=3/2*(x2+1/3)
Таким
образом: fX(x)=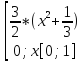 ,x[0;1]
,x[0;1]
Аналогично:
fУ(у)=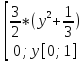 ,
у[0;1]
,
у[0;1]
3)
mx= fx(x)dx
mx=3/2
fx(x)dx
mx=3/2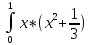 dx=3/2*(x4/4+x2/2)01=
dx=3/2*(x4/4+x2/2)01=
=3/4*(1/4+1/6)=5/8
mX=5/8; аналогично: my=5/8
M(5/8; 5/8)-центр распределения
4)D[X]=M[X2]-mx2;
M[X2]= =3/2
=3/2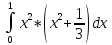 =
=
3/2*(x5/5-x3/9)01=3/2*(1/5+1/9)=7/15
D[X]=7/15-(5/8)2≈0,076
X=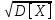 ≈0,276;аналогично:У≈0,276
≈0,276;аналогично:У≈0,276
5):
K[X;Y]=M[X*Y]-mx*my
.где
M[X*Y] =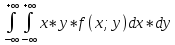
M[X*Y]=3/2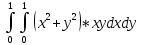 =3/2(
=3/2(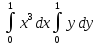 +
+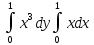 )=
)=
=3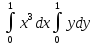 =3*(x4/401)*(y2/201)=3*1/4*1/2=3/8
=3*(x4/401)*(y2/201)=3*1/4*1/2=3/8
K[X;Y]=3/8-25/64=-1/64
R[X;Y]=xy=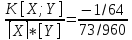 =
=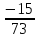 ≈-0,205
≈-0,205
6)Т.к.
K[X;Y]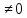 .то
Х и У зависимые
.то
Х и У зависимые
