Закон сохранения импульса. Реактивное движение |
161 |
Идея использования ракет для космических полетов развивалась уже в начале ХХ в. Русский ученый К. Э. Циолковский (1857—1935) разработал схему многоступенчатой ракеты, рассмотрел влияние атмосферы на ее движение, подтвердил расчетами реальность выхода в космическое пространство с помощью ракет, высказал идею создания околоземных станций.
4 октября 1957 |
г. в СССР под руководством С. П. Королева был з пущен |
|
а |
|
т |
первый в мире искусственный спутник Земли, а 12 апреля 1961 г. был осущест- |
влен первый полет |
человека в космическом пространстве. Ле чик-космонавт |
Ю. А. Гагарин облетел земной шар на космическом корабле «Вос ок». В 1969 г.
американские астронавты Н. Армстронг и Э. Олдрин впервые в истории высади- |
лись на поверхность Луны. |
|
|
|
Ракетно-космические исследования стали неотъемлемой ечастью современной |
цивилизации. |
|
|
|
Среди космонавтов есть уроженцы Беларуси: П. И. Климукв, В. В. Коваленок, |
О. В. Новицкий. |
|
|
с |
|
|
|
Беларусь входит в число космических держ в. С космодрома «Байконур» |
|
|
я |
а |
22 июля 2012 г. на орбиту высотой 500 км был запущен Белорусский космиче- |
|
а |
|
ский аппарат (БКА) — спутник массой 400 кг. Он обеспечивает дистанционное |
зондирование территории Беларуси путем съемки из космоса. |
Главные выводы |
н |
|
|
|
|
|
|
|
|
1. |
Если сумма внешних сил рав а улю, то импульс системы сохраняется. |
2. |
Закон сохранения импульса можно применить к незамкнутым систе- |
мам, если внутренние силы значительно больше внешних. |
3. |
Реактивная сила в зникает при отделении от тела какой-либо его ча- |
сти с некото ой ск |
остьюд. |
1.ЧтоНпроизойдетас импульсом системы, если на нее перестанут действовать внешние силы?
2.В каких случаях к незамкнутой системе можно применять закон сохранения импульса?
3.В каких случаях сохраняется проекция импульса на данную координатную ось?
4.Какую силу называют реактивной? Приведите примеры.
5.За счет чего увеличивается скорость ракеты в процессе ее движения?
6.Почему для запуска космических кораблей используются многоступенчатые ракеты? р
Правообладатель Народная асвета
162 Законы сохранения
|
|
|
Примеры решения задач |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Два |
вагона |
массами m1 # 10 т и |
m2 # 20 т |
двигались по горизонталь- |
|
ному участку |
пути навстречу друг другу. Модули |
скорости |
движения вагонов |
|
v |
= 0,1 |
|
м |
|
и v |
2 |
= 0,2 |
м |
|
|
соответственно. Определите модуль и направление ско- |
|
|
|
|
|
|
1 |
|
|
|
с |
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рости движения вагонов после срабатывания автосцепки. |
|
|
|
|
|
а |
|
Дано: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
m |
= 10 т = 1 104 кг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m21 |
= 20 т = 2 104 кг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
v1 = 0,1 |
|
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v2 |
= 0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
— ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 228 |
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
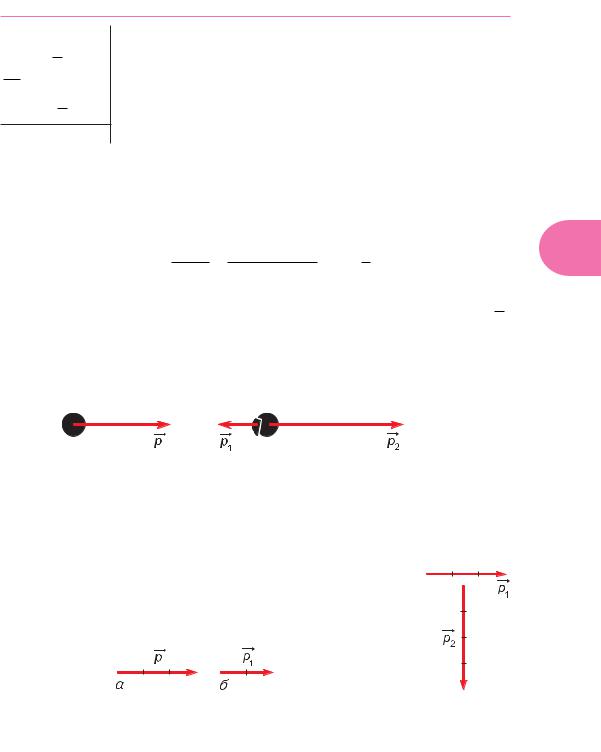
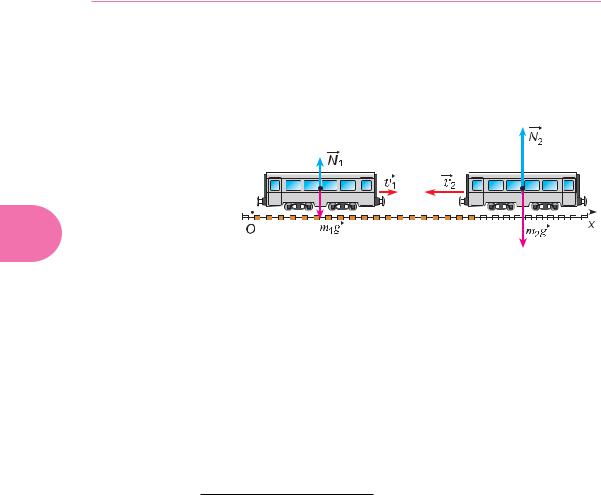
На систему из двух вагонов (рис. 228) действуют внешние силы: силы тя- |
|
|
|
|
|
|
r |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
r |
|
|
|
r |
|
жести m1g |
и |
m2 g |
и компенсирующие их силы ре кции |
N1 |
и N2 . Сила трения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
качения мала, ею можно пренебречь. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В итоге сумма внешних сил, действующих на вагоны, равна нулю. Значит, к |
|
системе из двух вагонов можно применить закон сохранения импульса: |
|
|
|
|
|
|
|
|
|
|
|
|
|
дн |
|
r |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m v |
+ mяv = |
(m + m )v. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
2 |
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь |
|
v |
— скорость ваго ов после сцепки. В проекции на ось Ох получим: |
|
|
|
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
m1v1 − m2 v2 = (m1 + m2 )vx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v = |
m1v1 |
− m2 v2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
m1 |
+ m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
0,1 м − 2 104 кг 0,2 м |
|
|
|
0,1 м − 0,4 м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
1 104 кг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
= |
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
с |
= |
|
|
с |
|
с |
|
= −0,1 м. |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
(1 + 2) 104 кг |
|
|
|
|
|
|
|
|
3,0 |
|
|
|
|
|
|
|
|
|
с |
|
|
|
Зн к «−» ук зывает на то, что после автосцепки вагоны будут двигаться про- |
|
|
Н m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тивоположно н правлению оси Ох. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
направлена противоположно оси Ох; v = 0,1 |
м |
|
|
|
|
|
|
|
|
|
|
|
Ответ: скорость v |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
2. Снаряд, вылетевший из пушки под углом к горизонту, разорвался в верх- |
|
ней точке траектории, имея скорость, модуль которой v = 100 |
м |
. Отношение масс |
|
|
|
осколков |
m2 |
= 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
Меньший из осколков полетел горизонтально в обратном на- |
|
|
|
|
правлении со скоростью, модуль которой v1 = 200 |
м |
. Определите модуль ско- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рости и направление движения большего осколка сразу после разрыва снаряда.
Правообладатель Народная асвета

164 Законы сохранения
3. Лодка массой m1 = 100 кг движется по озеру с постоянной скоростью, модуль которой v1 = 1,5 мс . С лодки прыгает мальчик массой m2 = 40 кг. Опре-
делите модуль скорости и направление движения лодки после прыжка мальчика, если мальчик прыгнет: а) с носа лодки в направлении ее движения со ско-
ростью, модуль которой |
|
= 2,0 |
м |
|
т |
v |
|
; б) так же, как в предыдущем случае, но |
|
|
|
|
|
|
|
2 |
|
с |
|
|
при v2 = 6,0 |
м |
; |
в) |
с кормы в направлении, противоположном движению лод- |
|
с |
|
м |
|
Определите также направление и модульаскорости, с ко- |
ки, при v2 = 2,0 |
|
. |
|
|
|
|
|
|
с |
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
торой должен прыгнуть мальчик, чтобы лодка остановилась. Все скорости рас-
но берега переместится плот, если человекапройдетспо плоту путь s = 6,0 м перпендикулярно берегу. Силой сопротивления воды пренебречь.
сматриваются в системе отсчета «берег». Силой сопротивл ния воды пре- |
небречь. |
е |
= 300 кг. На плоту |
4. На озере в состоянии покоя находит я плот ма |
ой m1 |
стоит человек массой m2 = 60 кг. Определите р тояние, на которое относитель-
5. Зенитный снаряд, выпущенный вертикально вверх, достиг максимальной высоты и взорвался. При этом образовалось три осколка одинаковой массы. Два осколка разлетелись симметрично под углом α = 60° к направлению полета сна-
|
ряда со скоростями, модули которых v1 = v2 = 300 |
м |
. Определите модуль и на- |
|
с |
|
|
я |
|
|
|
|
|
|
правление скорости третьего осколка. |
|
|
|
а |
|
|
|
§ 30. Работа силы. Мощ ость |
|
|
|
н |
|
|
|
|
В 7-м классе вы узнали о физической величине, называемой «работой». |
Как она определяетсяод? В каких единицах измеряется? Какое значение имеет для п актическ й деятельности человека?
Если н п вление силы совпадает с направлением движения тела, то работа,
которую соверш ет эта сила, равна произведению модуля силы на путь, прой- |
денный теломр: |
|
|
а |
А = Fs. |
|
|
|
Это вы знаете из 7-го класса. А если сила направлена под углом к переме- |
Н |
|
|
r |
щению? |
|
|
|
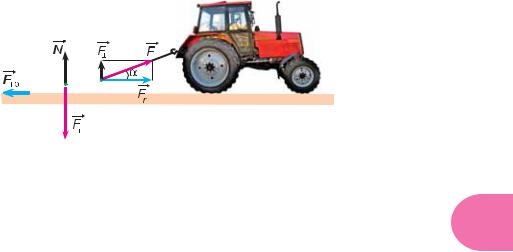
Рассмотрим пример. Трактор передвигает бетонный блок, действуя на него |
r |
|
|
r (рис. 232). Разложим |
силой F. Она составляет угол α с перемещением блока |
r |
r |
r |
|
силу F |
на две составляющие: Fr |
и F . |
|
Правообладатель Народная асвета
Работа силы. Мощность |
165 |
|
|
|
|
|
|
|
|
|
|
Рис. 232 |
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
а |
|
|
тело не перемещается. Эта сила работы не совер- |
В направлении силы F |
r |
|
|
|
|
|
|
|
r |
|
|
шает. Значит, работа силы F |
равна работе ее соста ляющ й |
т |
|
Fr , |
направленной |
по движению тела: |
|
|
A = Fr r. |
|
|
е |
|
|
|
|
|
|
|
|
|
|
Так как Fr = F cos α, то |
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = F r cos α. |
с |
|
|
|
(1) |
|
|
|
|
|
|
|
|
|
Работа равна модулю силы, умноженному на модуль перемещения и на ко- |
синус угла между силой и перемещением. |
а |
|
|
|
|
|
|
|
|
|
|
|
Формула (1) применима при постоянной силе и посто нном угле между силой и перемеще-
нием. В общем случае работу можно н йти, р збив я тр екторию движения тела на малые участ- |
|
я |
ки, вычисляя работы на этих участках по формуле (1) и суммируя их. |
Работа — скалярная величи а. а |
Единицей работы в СИ является 1 джоуль (1 Дж). Он равен работе, со- |
н |
|
вершаемой силой 1 ньют н при перемещении тела на 1 метр в направлении этой
силы (1 Дж = |
р |
|
1 Н м). |
|
|
Работа силы м жет бытьдп ложительной, отрицательной или равной нулю. |
а |
|
|
|
Это зависит от угла между силой и перемещением. Из формулы (1) следует: |
• если угол α ост |
оый, то работа положительна; |
|
• если прямой — |
авна нулю; |
|
Н |
|
|
r |
|
• если тупой — отрицательна. |
r |
В нашем примере на бетонный блок, кроме силы натяжения троса F, дейст- |
|
|
r |
r |
r |
вуют: сила тяжести Fт , сила реакции N и сила трения |
Fтр. Положительна, от- |
рицательна или равна нулю работа каждой из этих сил? Определите самостоятельно.
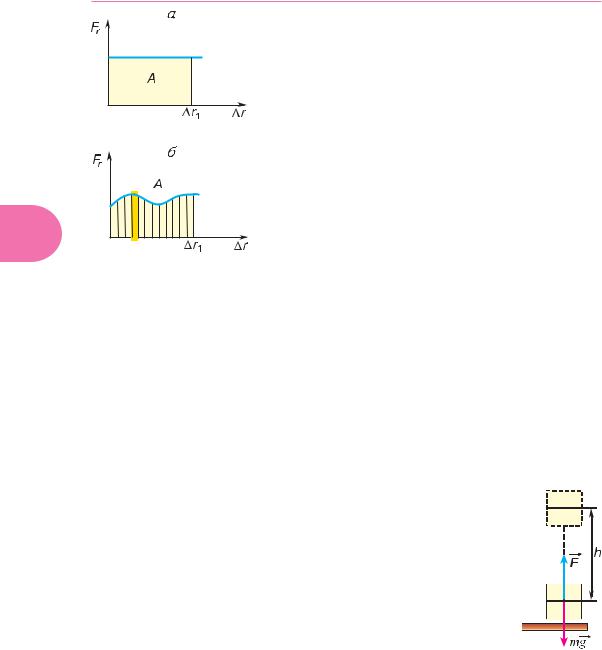
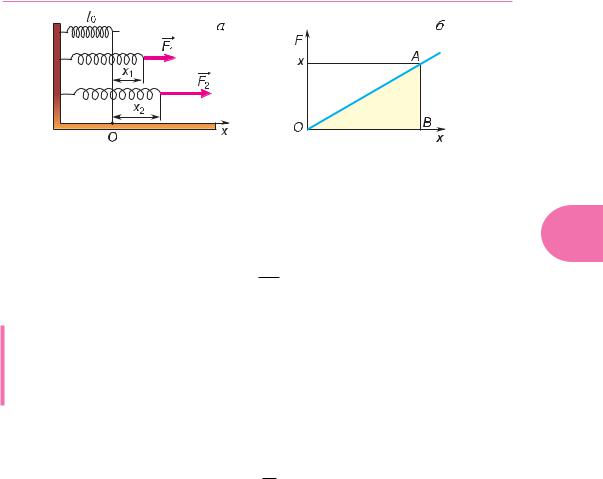
Построим график зависимости проекции силы F от модуля перемещения r при Fr = const. Из рисунка 233, а видно, что площадь закрашенного прямоугольника численно равна работе, совершенной этой силой при перемещении r1.
Правообладатель Народная асвета
Работа силы. Мощность |
|
|
|
|
|
|
|
|
|
167 |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 235 |
|
|
|
|
|
|
|
|
|
а |
2. Работа по деформированию пружины. Растянем пружину вн шней си- |
r |
|
|
|
|
|
|
|
|
|
|
лой F (рис. 235, а). При упругих деформациях модуль вн шн й силы прямо про- |
|
|
|
|
|
|
|
|
|
т |
|
порционален растяжению пружины х: F = kx , где k — жесткость пружины. Рабо- |
r |
|
|
|
|
|
|
|
|
|
|
та силы F численно равна площади треугольника ОАВ на графикеезависимости F |
от x (рис. 235, б). Так как ОВ = х, АВ = kx, то работа по ра тяжению пружины из |
ее недеформированного состояния |
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А = kx22 . |
|
с |
|
|
(3) |
Понятно, что равенство (3) выполн ется и для работы по сжатию пружины. |
|
|
|
|
|
а |
|
|
|
|
Работа силы зависит от выбора системы отсчета. Рассмотрим пример. Вы |
находитесь в кабине движущегося лифта. Совершает ли работу действующая на |
вас сила тяжести? Да, если определять р боту этой силы в системе отсчета, свя- |
|
|
|
|
я |
|
|
|
|
|
|
занной с Землей. Нет, если в системе отсчета, связанной с лифтом. Докажите |
это самостоятельно. |
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Быстроту совершения работы характеризует мощность. Мощностью назы- |
вают физическую величину, равнуюнотношению работы к промежутку времени, |
за который работа с вершена: |
|
|
|
|
|
|
|
|
|
|
д |
P = A . |
|
|
|
|
|
(4) |
|
|
|
|
t |
|
|
|
|
|
|
Мощность численно |
авна работе, совершаемой за единицу времени. |
|
о |
|
|
|
(1 Вт) — мощность, при ко- |
Единицей мощности в СИ является 1 ватт |
торой работа 1 джоуль совершается за 1 секунду. |
|
|
|
|
|
р |
|
|
единицы |
мощности: |
киловатт |
(1 кВт = |
Широко используются кратные |
= 1 103 Вт), мегаватт (1 МВт = 1 106 |
Вт). Мощность автомобильных двигателей |
а |
|
|
|
|
|
|
|
|
|
|
до сих пор указывают в лошадиных силах (л. с.). 1 л. с. ≈ 736 Вт. |
|
Работу можно выразить через мощность и время: A = P |
t. В связи с этим в |
качестве единицы работы часто используют 1 киловатт-час (1 кВт ч), равный |
3 600 000НДж. |
|
|
|
|
|
|
|
|
|
|
Именно за потребленное количество киловатт-часов (а не киловатт!) мы пла- |
тим ежемесячно при расчете за электроэнергию. |
|
|
|
|
|
Правообладатель Народная асвета

|
|
|
|
|
|
|
|
е |
а |
|
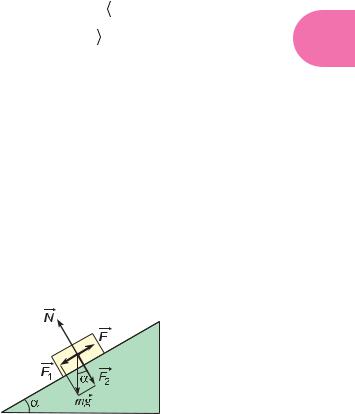
Рис. 236 |
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
ла. Из формул (1) и (4) |
Установим связь мощности со скоростью движ ния |
следует: P = |
F r cos α |
. |
Учитывая, что |
r |
= v, получим: |
т |
|
|
t |
|
|
t |
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
P = Fv cos α. |
|
|
|
|
(5) |
Равенство (5) показывает, что при одной и той же мощности двигателя можно: |
• либо двигаться с большой скоростью при ср внительно малой силе сопро- |
тивления движению (рис. 236, |
а); |
я |
|
• либо преодолевать большую силу сопротивления, двигаясь с небольшой |
скоростью (рис. 236, б). |
|
а |
|
|
|
|
|
|
|
|
|
|
Главные выводы |
н |
|
|
|
|
1. |
Работа силы рав произведению модулей силы и перемещения на ко- |
|
|
|
|
д |
|
|
синус угла между ними. |
|
|
|
2. |
Если угол меж у силой и перемещением острый, то работа силы поло- |
|
|
|
о |
|
|
|
жительна, если тупой — отрицательна. |
3. |
Силы, перпен икулярные перемещению тела, работу не совершают. |
4. |
|
р |
|
|
|
|
Мощн сть численно равна работе, совершаемой за единицу времени. |
5. |
Мощн сть п п рциональна произведению действующей силы и ско- |
а |
|
|
|
|
|
рости движения тела. |
|
|
|
Н |
|
|
|
|
|
|
Контрольные вопросы |
|
|
1. Положительной или отрицательной будет работа силы тяжести, действующей на тело, движущееся вверх? Падающее вниз? Почему?
2. Положительной или отрицательной будет работа силы сопротивления воздуха при движении мяча вверх? При его движении вниз? Почему?
3. Чему равна суммарная работа, которую совершила сила тяжести, действующая на брошенный вверх мяч, при его движении из точки бросания в верхнюю точку и обратно? 4. Совершает ли работу нормальная составляющая силы реакции поверхности, действующая на движущееся по этой поверхности тело? Почему?
5. Можно ли при заданной мощности выиграть и в силе, и в скорости одновременно?
Правообладатель Народная асвета
Работа силы. Мощность |
169 |
Примеры решения задач
1. Из колодца глубиной l = 12 м равномерно поднимают ведро воды массой
m1 = 10 кг с помощью каната, каждый метр которого имеет массу m0 = 0,20 кг. |
Определите совершенную при этом работу. Принять g = 10 |
|
м |
. |
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с2 |
т |
Дано: |
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 = 10 кг |
|
Учтем, |
|
что при подъеме ведра различные очки к н та |
l = 12 м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
проходят разные пути (от s = 0 для верхней очки каната до |
m0 = 0,20 кг |
s = l для его нижней точки). Тогда работа про ив сил яжести, |
l0 = 1,0 м |
действующих на ведро и канат: |
|
в |
|
|
|
|
|
|
|
|
|
|
|
g = 10 |
м |
|
|
|
|
|
|
|
|
|
A = m1gl + m2 g s , |
|
|
|
|
|
с2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где m = m |
|
l |
|
|
|
|
а |
= |
l |
|
|
|
|
|
|
|
|
|
|
|
— масса каната, |
s |
|
|
— среднее значение |
|
|
|
|
|
|
|
А — ? |
|
2 |
|
0 l |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
пути для точек каната. |
|
|
|
|
|
|
|
Отсюда A = m1 + |
m0l |
gl. |
|
|
|
|
|
|
|
|
|
|
|
|
|
2l0 |
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
0,20 кг 12 м |
|
|
|
|
|
|
|
|
|
|
|
|
A = 10 кг + |
10 |
м |
12 м =1344 Дж |
=1,3 кДж. |
|
|
2 1,0 м |
c2 |
Ответ: А = 1,3 кДж. |
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
2. Автомобиль массой m = 2,0 т, р звивяющий мощность Р = 40 л. с., подни- |
|
|
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
мается в гору с постоянной скоростью, модуль которой v = 3,0 м. Определите угол
наклона горы к горизонту. Силами сопротивления движению пренебречь. При- |
нять g = 10 |
|
м |
. |
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с2 |
|
|
|
|
|
|
|
|
|
|
Дано: |
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
m = 2,0 т = |
2,0 |
10 |
3 |
кг |
|
|
Сделаем рисунок к задаче (рис. 237). |
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
P = 40 л. с. = 2,9 |
104 Вт |
|
|
|
|
|
|
v = 3,0 |
|
м |
|
|
|
|
р |
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
g = 10 |
м |
|
|
|
|
|
|
|
|
|
|
с2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α — ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 237 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
МощностьНдвигателя P = Fv. Модуль силы F (см. рис. 237), движущей ав- |
томобиль, равен модулю составляющей силы тяжести: F1 = mg sin α. Тогда мощ- |
ность P = mgv sin α. |
|
|
|
|
|
|
|
|
Правообладатель Народная асвета

170 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Законы сохранения |
Отсюда sin α = |
|
P |
= |
|
|
2,9 |
104 Вт |
|
= 0,5; α = 30°. |
mgv |
|
|
3 |
|
м |
м |
|
|
|
|
|
|
|
|
|
|
Ответ: α = 30°. |
|
2,0 10 |
кг |
10 |
с2 |
|
3,0 с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
Упражнение 23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Какую работу по подъему штанги массой m = 200 кг на высоту h = 2,00 м |
совершила сила мускулов тяжелоатлета? Чему равна рабо |
|
силы яжести, дей- |
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
ствовавшей на штангу? Ускорение свободного падения в э ой и последующих за- |
дачах принять равным g = 10 |
м |
. |
|
|
|
|
|
|
|
тл жку на расстояние |
|
|
|
|
|
с2 |
|
|
|
|
|
|
|
|
2. Определите силу, с которой мальчик перем стил т |
|
|
|
|
|
|
|
|
|
|
с |
α = 30° к горизонту. Работа, |
l = 20,0 м. Сила постоянна и направлена под углом |
совершенная силой, равна А = 1,73 кДж. |
а |
|
|
|
|
3. Шарик массой |
m = 300 |
г |
скатывает я |
по |
наклонному желобу длиной |
l = 1,6 м с верхней точки желоба. При этом |
|
илавтяжести совершила работу |
А = 2,4 Дж. Определите угол наклона желоба к горизонту. |
|
|
|
|
|
|
|
|
|
я |
|
|
|
|
|
|
4. Какую минимальную работу необходимо совершить, чтобы растянуть пру- |
жину динамометра на x = 3 см, если показания динамометра при такой деформации пружины равны F = 8 Н?
5. Чтобы растянуть пружину дин мометра на 2 см, необходимо совершить работу 5 Дж. Какую работу нужно совершить, чтобы растянуть эту пружину еще
|
на 2 см? |
|
модуль которой v = 20,0 |
м |
|
|
6. Поезд, движущийся со скоростью, |
, начинает |
|
|
|
|
а |
|
с |
|
тормозить. Сила торможе ия постоянна, |
ее модуль F = 500 кН. До полной ос- |
тановки поезд прохо дит путьнs = 400 м. Определите массу поезда и работу силы
8.Почемуарводители груженых автомобилей преодолевают крутые подъемы наНм лой скорости?
9.Поддон с кирпичами массой m = 800 кг равномерно поднимают краном на девятый этаж строящегося дома. Высота одного этажа h0 = 3,5 м. Модуль скоро-l =тросастиминимальнуюторможения. о
высоту h 15 м с ускорением, направленным вертикально вверх. Модуль уско-
рения а = 0,6 м . Какую мощность развивает эта сила в конце подъема?
с2
Правообладатель Народная асвета