
vstatmp_engl
.pdf

268 10 Hypothesis Tests
frequency but for all frequencies up to k while the χ2 test with B 1 bins is rather insensitive to low frequency variations.
Remark: The alternative distribution quoted by Neyman was the exponential
|
Xi |
θiπi(z)! |
|
gk(z) = C exp |
k |
(10.10) |
|
|
=0 |
|
|
where C(θ) is a normalization constant. Neyman probably chose the exponential form, because it guaranties positivity without further restrictions of the parameters θi. Moreover, with this class of alternatives, it has been shown by E. S. Pearson [60] that the smooth test can be interpreted as a likelihood ratio test. Anyway, (10.8) or (10.10) serve only as a motivation to choose the test statistic (10.9) which is the relevant quantity.
10.3.8 The L2 Test
The binning-free tests discussed so far are restricted to one dimension, i.e. to univariate distributions. We now turn to multivariate tests.
A very obvious way to express the di erence between two distributions f and f0 is the integrated quadratic di erence
Z
L2 = [f(r) − f0(r)]2 dr. (10.11)
Unfortunately, we cannot use this expression for the comparison of a sample {r1, . . . , rN } with a continuous function f0. Though we can try to derive from our sample an approximation of f. Such a procedure is called probability density estimation (PDE ).
A common approach (see Chap. 12) is the Gaussian smearing or smoothing. The N discrete observations at the locations ri are transformed into the function
fG(r) = N1 X e−α(ri−r)2 .
The smearing produces a broadening which has also to be applied to f0:
Z
f0G(r) = f0(r′)e−α(r−r′)2 dr′ .
We now obtain a useful test statistic L2G,
Z
L2G = [fG(r) − f0G(r)]2 dr .
So far the L2 test [61] has not found as much attention as it deserves because the calculation of the integral is tedious. However its Monte Carlo version is pretty simple. It o ers the possibility to adjust the width of the smearing function to the density f0. Where we expect large distances of observations, the Gaussian width should be large, α f02.
A more sophisticated version of the L2 test is presented in [61]. The Monte Carlo version is included in Sect. 10.3.11, see below.


270 10 Hypothesis Tests
Fig. 10.11. K-nearest neighbor test.
10.3.10 The k-Nearest Neighbor Test
We consider two samples, one generated by a Monte Carlo simulation of a null distribution f0 and the experimental sample. The test statistic is the number n(k) of observations of the mixed sample where all of its k nearest neighbors belong to the same sample as the observation itself. This is illustrated in Fig. 10.11 for an unrealistically simple configuration. We find n(1) = 4 and n(2) = 4. The parameter k is a small number to be chosen by the user, in most cases it is one, two or three.
Of course we expect n to be large if the two parent distributions are very di erent. The k-nearest neighbor test is very popular and quite powerful. It has one caveat: We would like to have the number M of Monte Carlo observations much larger than the number N of experimental observations. In the situation with M N each observation tends to have as next neighbor a Monte Carlo observation and the test becomes less significant.
10.3.11 The Energy Test
A very general expression that measures the di erence between two distributions f(r) and f0(r) in an n dimensional space is
φ = |
1 |
Z |
dr Z |
dr′ [f(r) − f0(r)] [f(r′) − f0(r′)] R(r, r′) . |
(10.12) |
2 |
Here we call R the distance function. The factor 1/2 is introduced to simplify formulas which we derive later. The special case R = δ(r − r′) leads to the simple integrated quadratic deviation (10.11) of the L2 test
φ = |
1 |
Z |
dr [f(r) − f0(r)]2 . |
(10.13) |
2 |
10.3 Goodness-of-Fit Tests |
271 |
However, we do not intend to compare two distributions but rather two samples A {r1, . . . , rN }, B {r01, . . . , r0M }, which are extracted from the distributions f and f0, respectively. For this purpose we start with the more general expression (10.12) which connects points at di erent locations. We restrict the function R in such a way that it is a function of the distance |r − r′| only and that φ is minimum for f ≡ f0.
The function (10.12) with R = 1/|r − r′| describes the electrostatic energy of the sum of two charge densities f and f0 with equal total charge but di erent sign of the charge. In electrostatics the energy reaches a minimum if the charge is zero everywhere, i.e. the two charge densities are equal up to the sign. Because of this analogy we refer to φ as energy.
For our |
purposes the logarithmic function R(r) = |
− |
ln(r) and the bell function |
||||
|
2 |
) are more suitable than 1/r. |
|
||||
R(r) exp(−cr |
|
|
|
||||
We multiply the expressions in brackets in (10.12) and obtain |
|||||||
1 |
Z |
dr Z |
dr′ [f(r)f(r′) + f0(r)f0(r′) − 2f(r)f0(r′)] R(|r − r′|) . (10.14) |
||||
φ = |
|
||||||
2 |
|||||||
A Monte Carlo integration of this expression is obtained when we generate M random
points {r01 . . . r0M } of the distribution f0(r) and N random points {r1, . . . , rN } of the distribution f(r) and weight each combination of points with the corresponding
distance function. The Monte Carlo approximation is:
|
|
|
|
− |
|
X X |
|
|
1 |
Xi |
X |
|
|||||
φ ≈ |
|
|
1 |
|
|
|
|
i j>i R(|ri − rj |) − |
|
|
R(|ri − r0j |) + |
||||||
N(N |
|
|
1) |
|
NM |
|
j |
||||||||||
|
|
|
1 |
− |
|
|
Xi |
X |
|
|
|
|
|
|
|
||
+ |
|
|
|
|
R(|r0i − r0j |) |
|
|
|
|
|
|||||||
M(M 1) |
|
|
|
|
|
|
|||||||||||
|
|
|
X X |
|
j>i |
|
Xi |
X |
|
|
|||||||
|
1 |
|
|
|
1 |
|
|
||||||||||
≈ |
|
|
|
|
|
|
|
R(|ri − rj |) − |
|
|
|
R(|ri − r0j |) + |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
N2 |
|
i |
|
j>i |
NM |
|
|
j |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
+ |
1 |
|
Xi |
X |
R(|r0i − r0j |) . |
|
|
|
|
|
(10.15) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
M2 |
|
|
|
j>i |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
This is the energy of a configuration of discrete charges. Alternatively we can understand this result as the sum of three expectation values which are estimated by the two samples. The value of φ from (10.15) thus is the estimate of the energy of two samples that are drawn from the distributions f0 and f and that have the total charge zero.
We can use the expression (10.15) as test statistic when we compare the experimental sample to a Monte Carlo sample, the null sample representing the null distribution f0. Small energies signify a good, large ones a bad agreement of the experimental sample with H0. To be independent of statistical fluctuations of the simulated sample, we choose M large compared to N, typically M ≈ 10N.
The test statistic energy φ is composed of three terms φ1, φ2, φ3 which correspond to the interaction of the experimental sample with itself, to its interaction with the null sample and with the interaction of the null sample with itself:
φ = φ1 − φ2 + φ3 , |
(10.16) |
||||
|
1 |
− |
|
X |
(10.17) |
φ1 = |
N(N |
|
1) |
i<j R(|ri − rj|) , |
|

10.4 Two-Sample Tests |
275 |
4 |
c2 |
)=0.71 |
|
p( |
|
|
p( |
)=0.02 |
|
F |
|
2 |
|
|
0
-2 |
|
|
|
-4 |
-2 |
0 |
2 |
|
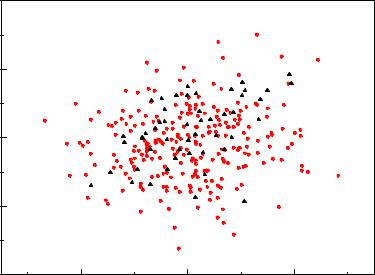
Fig. 10.14. Comparison of a normally distributed sample (circles) from H0 with a linear admixture (triangles) with the normal distribution of H0.
With a χ2 test with 9 bins we obtain a p-value of 71%. It is unable to identify the deformation of f0.
More detailed investigations can be found in [62].
10.4 Two-Sample Tests
10.4.1 The Problem
A standard situation in particle physics is that H0 cannot be compared directly to the data but has first to be transformed to a Monte Carlo sample, to take into account acceptance losses and resolution e ects. We have to compare two samples, a procedure which we had already applied in the energy test. Here the distribution of the test statistic needed to compute p-values can be generated by a simple Monte Carlo program.
In other sciences, a frequently occurring problem is that the e ectiveness of two or several procedures have to be compared. This may concern drugs, animal feed or the quality of fabrication methods. A similar problem is to test whether a certain process is stable or whether its results have changed during time. Also in the natural sciences we frequently come across the problem that we observe an interesting phenomenon in one data sample which apparently has disappeared in another sample taken at a later time. It is important to investigate whether the two data samples are compatible with each other. Sometimes it is also of interest to investigate whether a Monte Carlo sample and an experimental sample are compatible. Thus we are interested in

276 10 Hypothesis Tests
a statistical procedure which tells us whether two samples A and B are compatible, i.e. drawn from the same parent distribution. Thereby we assume that the parent distribution itself is unknown. If it were known, we could apply one of the GOF tests which we have discussed above. We have to invent procedures to generate the distribution of the test statistic. In some cases this is trivial. In the remaining cases, we have to use combinatorial methods.
10.4.2 The χ2 Test
To test whether two samples are compatible, we can apply the χ2test or the Kolmogorov–Smirnov test with minor modifications.
When we calculate the χ2 statistic we have to normalize the two samples A and B of sizes N and M to each other. For ai and bi entries in bin i, ai/N − bi/M should be compatible with zero. With the usual error propagation we obtain an estimate ai/N2 + bi/M2 of the quadratic error of this quantity and
|
Xi |
|
|
|
|
χ2 = |
B |
(ai/N |
− bi/M)2 |
. |
(10.22) |
|
=1 |
(ai/N2 |
+ bi/M2) |
|
|
|
|
|
|
|
|
It follows approximately a a χ2 distribution of B − 1 degrees of freedom, but not exactly, as we had to replace the expected values by the observed numbers in the error estimation. We have to be careful if the number of observations per bin is small.
10.4.3 The Likelihood Ratio Test
The likelihood ratio test is less vulnerable to low event numbers than the χ2 test.
Setting r = M/N we compute the likelihood that we observe in a single bin a entries with expectation λ and b entries with expectation ρλ, where the hypothesis H0 is characterized by ρ = r:
L(λ, ρ|a, b) = e−λλa e−ρλ(ρλ)b . a! b!
Leaving out constant factors the log-likelihood is
ln L = −λ(1 + ρ) + (a + b) ln λ + b ln ρ .
We determine the conditional maximum likelihood value of λ under ρ = r and the corresponding log-likelihood:
1 + r = (a + b) |
1 |
, |
|
|
||
|
|
|
||||
ˆ |
|
|
||||
|
|
|
λc |
|
|
|
ˆ |
a + b |
|
|
|
|
|
λc = |
|
, |
|
|
|
|
1 + r |
|
|
|
+ b ln r . |
||
ln Lcmax = (a + b) −1 + ln |
a + b |
|||||
|
||||||
1 + r |
||||||
The unconditional maximum of the likelihood is found for ˆ and :
λ = a ρˆ = b/a
