
vstatmp_engl
.pdf11.3 |
Linear Factor Analysis and Principal Components 307 |
||||
|
|
− |
N |
||
|
|
X |
|||
δp2 |
|
1 |
|
|
|
= |
N 1 |
(Xnp − Xp)2 . |
|||
|
|
|
n=1 |
||
The quantity xnp is the normalized deviation of the measurement value of type p for the object n from the average over all objects for this measurement.
In the same way as in Chap. 4 we construct the correlation matrix for our sample by averaging the P × P products of the components xn1 . . . xnP over all N objects:
C = |
|
1 |
|
XT X |
, |
|
|||||
N − 1 |
|||||
|
|
− |
|
N |
|
|
|
|
X |
|
|
Cpq = |
|
1 |
|
|
xnpxnq . |
N |
|
1 |
n=1 |
||
|
|
|
|
|
|
It is a symmetric positive definite P × P matrix. Due to the normalization the diagonal elements are equal to unity.
Then this matrix is brought into diagonal form by an orthogonal transformation corresponding to a rotation in the P -dimensional feature space.
C → VT CV = diag(λ1 . . . λP ) .
The uncorrelated feature vectors in the rotated space yn = {yn1, . . . , ynP } are given by
yn = VT xn , xn = Vyn .
To obtain eigenvalues and -vectors we solve the linear equation system |
|
(C − λpI)vp = 0 , |
(11.14) |
where λp is the eigenvalue belonging to the eigenvector vp:
Cvp = λpvp .
The P eigenvalues are found as the solutions of the characteristic equation det(C − λI) = 0 .
In the simple case described above of only two features, this is a quadratic equation
|
C11 − λ |
− |
|
|
|
C12 |
|
= 0 , |
|
|
C21 |
C22 |
|
|
|
λ |
|
that fixes the two eigenvalues. The eigenvectors are calculated from (11.14) after substituting the respective eigenvalue. As they are fixed only up to an arbitrary factor, they are usually normalized. The rotation matrix V is constructed by taking the eigenvectors vp as its columns: vqp = (vp)q.
Since the eigenvalues are the diagonal elements in the rotated, diagonal correlation matrix, they correspond to the variances of the data distribution with respect to the principal axes. A small eigenvalue means that the projection of the data on this axis has a narrow distribution. The respective component is then, presumably, only of small influence on the data, and may perhaps be ignored in a model of the data. Large eigenvalues belong to the important principal components.
Factors fnp are obtained by standardization of the transformed variables ynp by division by the square root of the eigenvalues λp:
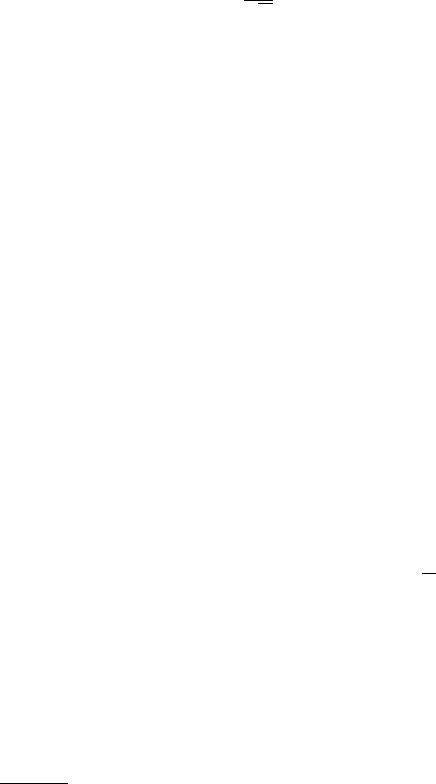
11.4 Classification |
309 |
1.The transformation of the correlation matrix to diagonal form makes sense, as we obtain in this way uncorrelated inputs. The new variables help to understand better the relations between the various measurements.
2.The silent assumption that the principal components with larger eigenvalues are the more important ones is not always convincing, since starting with uncorrelated measurements, due to the scaling procedure, would result in eigenvalues which are all identical. An additional di culty for interpreting the data comes from the ambiguity (11.16) concerning rotations of factors and loadings.
11.4 Classification
We have come across classification already when we have treated goodness-of-fit. There the problem was either to accept or to reject a hypothesis without a clear alternative. Now we consider a situation where we dispose of information of two or more classes of events.
The assignment of an object according to some quality to a class or category is described by a so-called categorical variable. For two categories we can label the two possibilities by discrete numbers; usually the values ±1 or 1 and 0 are chosen. In most cases it makes sense, to give as a result instead of a discrete classification a continuous variable as a measure for the correctness of the classification. The classification into more than two cases can be performed sequentially by first combining classes such that we have a two class system and then splitting them further.
Classification is indispensable in data analysis in many areas. Examples in particle physics are the identification of particles from shower profiles or from Cerenkov ring images, beauty, top or Higgs particles from kinematics and secondaries and the separation of rare interactions from frequent ones. In astronomy the classification of galaxies and other stellar objects is of interest. But classification is also a precondition for decisions in many scientific fields and in everyday life.
We start with an example: A patient su ers from certain symptoms: stomachache, diarrhoea, temperature, head-ache. The doctor has to give a diagnosis. He will consider further factors, as age, sex, earlier diseases, possibility of infection, duration of the illness, etc.. The diagnosis is based on the experience and education of the doctor.
A computer program which is supposed to help the doctor in this matter should be able to learn from past cases, and to compare new inputs in a sensible way with the stored data. Of course, as opposed to most problems in science, it is not possible here to provide a functional, parametric relation. Hence there is a need for suitable methods which interpolate or extrapolate in the space of the input variables. If these quantities cannot be ordered, e.g. sex, color, shape, they have to be classified. In a broad sense, all this problems may be considered as variants of function approximation.
The most important methods for this kind of problems are the discriminant analysis, artificial neural nets, kernel or weighting methods, and decision trees. In the last years, remarkable progress in these fields could be realized with the development of support vector machines, boosted decision trees, and random forests classifiers.
Before discussing these methods in more detail let us consider a further example.

11.4 Classification |
311 |
of validation, cross validation and bootstrap ( see Sect.12.2), have been developed which permit to use the full sample to adjust the parameters of the method. In an n-fold cross validation the whole sample is randomly divided into n equal parts of N/n events each. In turn one of the parts is used for the validation of the training result from the other n − 1 parts. All n validation results are then averaged. Typical choices are n equal to 5 or 10.
11.4.1 The Discriminant Analysis
The classical discriminant analysis as developed by Fisher is a special case of the classification method that we introduce in the following. We follow our discussions of Chap. 6, Sect. 6.3.
If we know the p.d.f.s f1(x) and f2(x) for two classes of events it is easy to assign an observation x to one of the two classes in such a way that the error rate is minimal (case 1):
x→ class 1, if f1(x) > f2(x) ,
x→ class 2, if f1(x) < f2(x) .
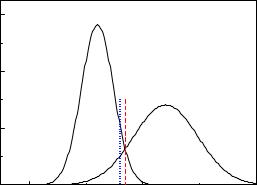
Normally we will get a di erent number of wrong assignments for the two classes: observations originating from the broader distribution will be miss-assigned more often, see Fig. 11.8) than those of the narrower distribution. In most cases it will matter whether an input from class 1 or from class 2 is wrongly assigned. An optimal classification is then reached using an appropriately adjusted likelihood ratio:
x→ class 1, if f1(x)/f2(x) > c ,
x→ class 2, if f1(x)/f2(x) < c .
If we want to have the same error rates (case 2), we must choose the constant c such that the integrals over the densities in the selected regions are equal:
Z Z
f1(x)dx = f2(x)dx . (11.17)
f1/f2>c f1/f2<c
This assignment has again a minimal error rate, but now under the constraint (11.17). We illustrate the two possibilities in Fig. 11.8 for univariate functions.
For normal distributions we can formulate the condition for the classification explicitly: For case 2 we choose that class for which the observation x has the smallest distance to the mean measured in standard deviations. This condition can then be written as a function of the exponents. With the usual notations we get
(x − µ1)T V1(x − µ1) − (x − µ2)T V2 |
(x − µ2) < 0 → class 1 , |
(x − µ1)T V1(x − µ1) − (x − µ2)T V2 |
(x − µ2) > 0 → class 2 . |
This condition can easily be generalized to more than two classes; the assignment according to the standardized distances will then, however, no longer lead to equal error rates for all classes.
The classical discriminant analysis sets V1 = V2. The left-hand side in the above relations becomes a linear combination of the xp. The quadratic terms cancel. Equating it to zero defines a hyperplane which separates the two classes. The sign of this
312 11 Statistical Learning
0.3 |
|
|
|
|
|
f |
|
|
|
1 |
|
0.2 |
|
|
|
f(X) |
|
|
f |
|
|
|
2 |
0.1 |
|
|
|
0.0 |
0 |
10 |
20 |
|
|||
|
|
X |
|
Fig. 11.8. Separation of two classes. The dashed line separates the events such that the error rate is minimal, the dotted line such that the wrongly assigned events are the same in both classes.
linear combination thus determines the class membership. Note that the separating hyperplane is cutting the line connecting the distribution centers under a right angle only for spherical symmetric distributions.
If the distributions are only known empirically from representative samples, we approximate them by continuous distributions, usually by a normal distribution, and fix their parameters to reproduce the empirical moments. In situations where the empirical distributions strongly overlap, for instance when a narrow distribution is located at the center of a broad one, the simple discriminant analysis does no longer work. The classification methods introduced in the following sections have been developed for this and other more complicated situations and where the only source of information on the population is a training sample. The various approaches are all based on the continuity assumption that observations with similar attributes lead to similar outputs.
11.4.2 Artificial Neural Networks
Introduction
The application of artificial neural networks, ANN, has seen a remarkable boom in the last decades, parallel to the exploding computing capacities. From its many variants, in science the most popular are the relatively simple forward ANNs with back-propagation, to which we will restrict our discussion. The interested reader should consult the broad specialized literature on this subject, where fascinating self organizing networks are described which certainly will play a role also in science, in the more distant future. It could e.g. be imagined that a self-organizing ANN would be able to classify a data set of events produced at an accelerator without human intervention and thus would be able to discover new reactions and particles.


314 11 Statistical Learning
x1 |
w(1)11 |
w(2)11 |
|
|
y1 |
|
|
s |
w(2)12 |
s |
|
||
|
||||||
|
|
|||||
|
w(1)12 |
|
|
|||
x2 |
|
s |
|
s |
|
y2 |
|
|
|
||||
x3 |
|
s |
|
s |
|
y3 |
|
|
|
||||
|
|
|
|
|
||
xn |
w(1)n3 |
s |
ym |
s |
Fig. 11.9. Back propagation. At each knot the sigmoid function of the sum of the weighted inputs is computed.
to it is calculated. Each knot symbolizes a non-linear so-called activation function x′i = s(ui), which is identical for all units. The first layer produces a new data vector x′. The second layer, with m′ knots, acts analogously on the outputs of the first one. We call the corresponding m × m′ weight matrix W(2). It produces the output vector y. The first layer is called hidden layer, since its output is not observed directly. In principle, additional hidden layers could be implemented but experience shows that this does not improve the performance of the net.
The net executes the following functions: |
|
|
||||
|
xj′ = s |
k |
Wjk(1)xk! , |
|
|
|
|
|
X |
Wij(2)xj′ . |
|
|
|
|
yi = s |
j |
|
|
||
This leads to the final result: |
|
X |
|
|
|
|
X |
|
|
X |
! |
|
|
|
|
|
|
|||
yi = s |
|
Wij(2)s |
Wjk(1)xk |
. |
(11.18) |
|
|
|
|
|
k |
|
|
|
j |
|
|
|
|
|
Sometimes it is appropriate to shift the input of each unit in the first layer by a constant amount (bias). This is easily realized by specifying an artificial additional input component x0 ≡ 1.
The number of weights (the parameters to be fitted) is, when we include the component x0, (n + 1) × m + mm′.
Activation Function
The activation function s(x) has to be non-linear, in order to achieve that the superposition (11.18) is able to approximate widely arbitrary functions. It is plausible

11.4 Classification |
315 |
|
1.2 |
|
|
|
|
|
|
|
|
1.0 |
|
|
|
|
|
|
|
|
0.8 |
|
|
|
|
|
|
|
s |
0.6 |
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
0.0 |
-6 |
-4 |
-2 |
0 |
2 |
4 |
6 |
|
|
|||||||
|
|
|
|
|
x |
|
|
|
Fig. 11.10. Sigmoid function.
that it should be more sensitive to variations of the arguments near zero than for very large absolute values. The input bias x0 helps to shift input parameters which have a large mean value into the sensitive region. The activation function is usually standardized to vary between zero and one. The most popular activation function is the sigmoid function
1 s(u) = e−u + 1 ,
which is similar to the Fermi function. It is shown in Fig. 11.10.
The Training Process
In the training phase the weights will be adapted after each new input object. Each time the output vector of the network y is compared with the target vector yt. We define again the loss function E:
E = (y − yt)2, |
(11.19) |
which measures for each training object the deviation of the response from the expected one.
To reduce the error E we walk downwards in the weight space. This means, we change each weight component by ΔW , proportional to the sensitivity ∂E/∂W of E to changes of W :
ΔW = − 12 α∂W∂E
∂y = −α(y − yt) · ∂W .
The proportionality constant α, the learning rate, determines the step width. We now have to find the derivatives. Let us start with s:
ds |
|
e−u |
(11.20) |
|
|
= |
|
= s(1 − s) . |
|
du |
(e−u + 1)2 |
|||
From (11.18) and (11.20) we compute the derivatives with respect to the weight components of the first and the second layer,
316 11 Statistical Learning
|
|
|
|
∂yi |
= y |
(1 |
− |
y |
)x′ |
, |
|
|
|||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
∂W |
(2) |
|
|
i |
|
i |
j |
|
|
|
|
|
|
|
|
ij |
|
|
|
|
|
|
|
|
|
|
|
and |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂yi |
= y |
(1 |
− |
y |
)x′ |
W |
(2)(1 |
− |
x′ |
)x . |
||||
|
|
|
|||||||||||||
|
∂W |
(1) |
|
i |
|
i |
|
j |
|
ij |
|
j |
k |
||
|
|
jk |
|
|
|
|
|
|
|
|
|
|
|
|
|
It is seen that the derivatives depend on the same quantities which have already been calculated for the determination of y (the forward run through the net). Now we run backwards, change first the matrix W(2) and then with already computed quantities also W(1). This is the reason why this process is called back propagation. The weights are changed in the following way:
Wjk(1) |
→ Wjk(1) |
− α(y |
− yt) Xi |
yi(1 − yi)xj′ Wij(2)(1 − xj′ )xk , |
|||||||||
W |
(2) |
→ |
W |
(2) |
− |
α(y |
− |
y |
)y |
(1 |
− |
y |
)x′ . |
|
ij |
|
ij |
|
t |
i |
|
i |
j |
||||
Testing and Interpreting
The gradient descending minimum search has not necessarily reached the minimum after processing the training sample a single time, especially when the available sample is small. Then the should be used several times (e.g. 10 or 100 times). On the other hand it may happen for too small a training sample that the net performs correctly for the training data, but produces wrong results for new data. The network has, so to say, learned the training data by heart. Similar to other minimizing concepts, the net interpolates and extrapolates the training data. When the number of fitted parameters (here the weights) become of the same order as the number of constraints from the training data, the net will occasionally, after su cient training time, describe the training data exactly but fail for new input data. This e ect is called over-fitting and is common to all fitting schemes when too many parameters are adjusted.
It is therefore indispensable to validate the network function after the optimization, with data not used in the training phase or to perform a cross validation. If in the training phase simulated data are used, it is easy to generate new data for testing. If only experimental data are available with no possibility to enlarge the sample size, usually a certain fraction of the data is reserved for testing. If the validation result is not satisfactory, one should try to solve the problem by reducing the number of network parameters or the number of repetitions of the training runs with the same data set.
The neural network generates from the input data the response through the fairly complicated function (11.18). It is impossible by an internal analysis of this function to gain some understanding of the relation between input and resulting response. Nevertheless, it is not necessary to regard the ANN as a “black box”. We have the possibility to display graphically correlations between input quantities and the result, and all functional relations. In this way we gain some insight into possible connections. If, for instance, a physicist would have the idea to train a net with an experimental data sample to predict for a certain gas the volume from the pressure and the temperature, he would be able to reproduce, with a certain accuracy, the results of the van-der-Waals equation. He could display the relations between the
