3. Поверхности

Мир поверхностей разнообразен и безграничен. Он простирается от простейшей поверхности – плоскости, до сложнейших, причудливых форм криволинейных поверхностей, не поддающихся точному математическому описанию. Под поверхностью мы будем понимать границу материального тела, не имеющую третьего измерения – толщины. Поверхность можно задать следующими способами: аналитическим; кинематическим; каркасным.

Аналитический способ задания поверхностей рассматривается в соответствующих разделах курса высшей математики. Под кинематическим способом задания поверхностей подразумевается «след» непрерывно перемещающейся линии в пространстве по определенному закону. Закон движения перемещающейся линии – образующей, может определять другая линия (или линии) – направляющая. При этом подразумевается, что образующая скользит по направляющей.

Каркасный способ задания поверхности упрощенно можно представить как набор линий – продольных и поперечных.

Кинематический способ задания поверхности подводит к понятию определителя поверхности, который состоит из двух частей: геометрической и алгоритмической. Геометрическая часть определяет вид и способ задания образующей и направляющей. Алгоритмическая часть определяет закон движения образующей.

3.1. Многогранники

В определении понятия многогранники существует несколько суждений. Рассматривая заданиеповерхности многогранника с позиций кинематического способа, можно сказать следующее. Движение прямолинейной образующей по ломаной направляющей образует гранную поверхность. Если образующая движется по направляющей «параллельно самой себе», поверхность называется призматической. Если одна точка образующей закреплена неподвижно – поверхность называется пирамидальной. [2, стр. 62]

В некоторых учебниках вместо поверхности многогранников рассматривается геометрическое тело, ограниченное со всех сторон плоскими многоугольниками [8, стр. 105]. Плоские многоугольники, ограничивающие многогранник, являются его гранями, а линии пересечения граней – его ребрами.

3.1.1. Определение видимости ребер многогранника

Прежде, чем решать задачи с многогранниками, необходимо определить видимость ребер.

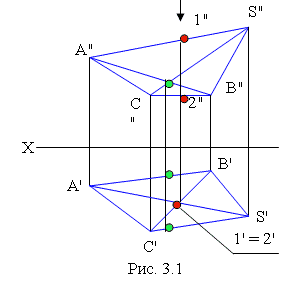
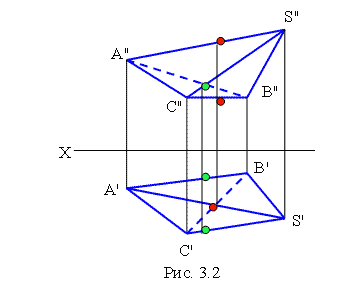
На рис. 3.1. задана трехгранная пирамида SABC. Для определения видимости ребер AS и BC на горизонтальной плоскости проекций воспользуемся горизонтально конкурирующими точками (их проекциями) 1' = 2' . Пусть 1 принадлежит ребру AS а 2 принадлежит BC. Перенесем точки на фронтальную плоскость и по направлению стрелки отмечаем, что точка 1 расположена выше точки 2, следовательно, на горизонтальной проекции ребро AS будет видимым. Аналогично определяется видимость ребер для фронтальной плоскости. На рис. 3.2 выполнено построение пирамиды с учетом видимости ребер.

 

3.1.2. Принадлежность точки к поверхности многогранника

Все грани многогранников представляют собой плоскости, поэтому для построения прямых и точек, принадлежащих граням поверхности, необходимо воспользоваться решением, рассмотренным в теме 1.3.2., рис. 1.23 - принадлежность точки к плоскости.