4.2.2. Пересечение прямой общего положения с плоскостью общего положения

При решении позиционных задач надо помнить, что пересечением двух множеств являются точки, одновременно принадлежащие этим множествам. Отсюда: если прямая принадлежит плоскости, то их пересечением является сама прямая, так как все точки прямой одновременно принадлежат самой прямой и плоскости.

На рис. 4.7 заданы плоскость общего положения АВС и прямая общего положения DE. Для нахождения их точки пересечения воспользуемся общим алгоритмом.

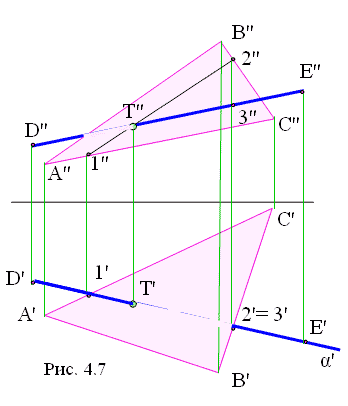
Согласно алгоритму необходимо задать вспомогательную поверхность (в нашем случае плоскость) – посредник.

Для того чтобы плоскость-посредник пересекла заданные фигуры по прямым линиям, а это требование алгоритма, ее задаем через прямую DE.

1. Задаем горизонтально проецирующую плоскость α' = D'E'.

2. Пересечение плоскости α' с прямой DE – сама прямая, а с плоскостью АВС пересечение обозначим точками 1' 2' (см. рис. 4.6). Построим линию 1" 2" на фронтальной плоскости.

3. Отмечаем точки взаимного пересечения построенных линий: точка Т (Т") является результатом пересечения построенных линий D"E" с линией 1" 2".

4. Определяем видимость прямой DE и плоскости АВС. Для горизонтальной плоскости можно воспользоваться конкурирующими точками 2' = 3'. По направлению проецирующих лучей на горизонтальную плоскость проекций видим, что точка 2, принадлежащая ВС, расположена выше, следовательно, на горизонтальной проекции ВС – видимая, а DE от точки 3 до точки Т – невидимая. Аналогично определяется видимость для фронтальной плоскости. Подробно алгоритм решения этой задачи приведен в работе Андрющенко К.Е. «Начертательная геометрия. Учебный курс. Пересечение прямой с плоскостью».

4.2.3. Взаимное пересечение плоскостей общего положения

Линия взаимного пересечения двух плоскостей заданных тремя точками находится по принципу рассмотренной выше задачи. Для чего надо дважды решить задачу на пересечение прямой с плоскостью.

Подробно алгоритм решения этой задачи приведен в работе Андрющенко К.Е. «Начертательная геометрия. Учебный курс. Пересечение плоскостей».

Для нахождения линии пересечения плоскостей заданных следами надо найти две точки, одновременно принадлежащие плоскостям. Этими точками являются точки пересечения следов. На рис. 4.8 заданы плоскости α и β. Отмечаем точки пересечения следов N (N" N' ) и Т (Т" Т'). Линия ТN является результатом пересечения этих плоскостей.

Другие примеры пересечения плоскостей см. в работе [2, стр. 43].

4.3. Пересечение прямой линии общего положения с поверхностями

Для определения точек пересечения прямой линии с поверхностями в качестве поверхности – посредника используется плоскость.

На рис. 4.9 заданы поверхность пирамиды и прямая m. Здесь уместно напомнить порядок решения задачи на пересечение прямой с плоскостью (см. рис. 4.7). и порядок решения задачи на пересечение проецирующей плоскости с гранной поверхностью (см. рис. 4.2). По существу надо объединить эти задачи. В качестве примера приведен чертеж пирамиды из подраздела 4.1. Итак, решение:

1. Через прямую m проводим фронтально проецирующую плоскость f_oa''.

2. Строим линии пересечения вспомогательной f_oa'' с пирамидой и с прямой m.

3. Отмечаем точки пересечения построенных линий (на рис. 4.9 это D (D') и E (E')).

4. Определяем видимость прямой относительно пирамиды.

В некоторых случаях, если вспомогательная проецирующая плоскость, проведенная через прямую линию, не может пересечь заданную поверхность по простым линиям, прибегают к способам преобразования прямоугольных проекций.

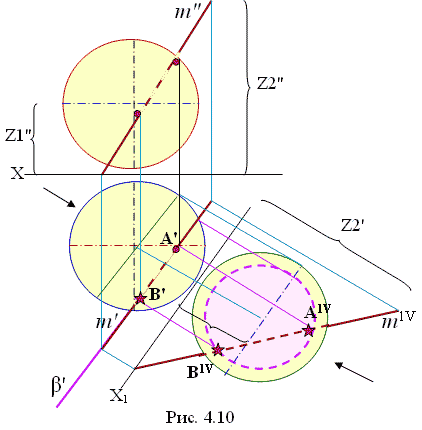
На рис. 4.10 заданы прямая АВ и поверхность сферы. Ни фронтально проецирующая, ни горизонтально проецирующая плоскости, проведенные через прямую, не дают в проекции простую линию – окружность, несмотря на то, что в пространстве эти плоскости пересекают сферу по окружностям. Для решения этой задачи надо выполнить преобразование: заданную прямую преобразовать в прямую уровня. На рис. 4.10 выполнена замена плоскостей проекций. Введена новая плоскость проекций π₄ перпендикулярно к π₁. В новой Х₁ (π₁/ π₄) проведена плоскость уровня β' , которая пересекла сферу по окружности и на π₄ эта окружность отобразилась в натуральную величину. Далее, согласно алгоритму, отмечаем точки пересечения построенных линий – А^1V, В^1V. По линиям связи переносим их на горизонтальную - А¹, В¹ и на фронтальную (буквами не обозначены). Последний пункт алгоритма – определяем видимость прямой относительно сферы.

 

В некоторых случаях в качестве поверхностей – посредников применяют плоскости общего положения. Если плоскость, пересекающая пирамиду или конус, проходит через их вершину, то независимо от того, является ли она плоскостью общего положения или частного, результатом пересечения будут две пересекающиеся прямые. Аналогично, если плоскость, пересекающая призму или цилиндр, расположена параллельно ребру призмы или параллельно образующей цилиндра, то независимо от того, является ли она плоскостью общего положения или частного, результатом пересечения будут две прямые параллельные ребрам призмы или образующей цилиндра. Именно это обстоятельство используется при решении задач на пересечение прямой общего положения с указанными поверхностями .

  

На рис. 4.11 заданы поверхность конуса и прямая общего положения АВ. Для решения этой задачи воспользуемся вспомогательной плоскостью–посредником общего положения и зададим ее через вершину конуса S и через прямую АВ. Для этого через вершину конуса и точку А" зададим прямую. Таким образом, образовалась плоскость SAB общего положения, заданная двумя пересекающимися прямыми. Принимая во внимание, что основание конуса принадлежит горизонтальной плоскости проекций, найдем горизонтальный след вспомогательной плоскости М=М' - В=В', который пересечет основание конуса в точках 1 (1') и 2 (2'). Поверхность конуса вспомогательная плоскость пересечет по проекциям образующихS'2' и S'1'. Отмеченные образующие и прямая АВ принадлежат вспомогательной плоскости, следовательно, точки их пересечения с прямой AB являются точками пересечения этой прямой с поверхностью конуса.

Другие примеры пересечения прямой линии общего положения с поверхностями см. в [2, стр. 79].