5. Метрические задачи
В разделе 4 отмечалось, что метрическими называются задачи, решение которых связано с нахождением характеристик геометрических фигур, измеряемых линейными и угловыми величинами. Все многообразие метрических задач в конечном итоге сводится к двум видам: задачам на определение расстояний между двумя точками и задачам на нахождение величины угла между двумя пересекающимися прямыми. К метрическим задачам также относятся задачи на построение геометрических фигур по наперед заданным размерам (задачи геометрического конструирования).
5.1. Определение расстояний
Определение расстояний между точкой и прямой, двумя параллельными прямыми, точкой и плоскостью, прямой и плоскостью, двумя плоскостями, скрещивающимися прямыми, в конечном итоге сводится к нахождению кратчайшего расстояния между двумя точками. Кратчайшее расстояние определяется перпендикуляром между точкой и прямой, точкой и плоскостью, двумя параллельными прямыми и плоскостями.
5.1.1. Взаимно перпендикулярные прямые
Для построения взаимно перпендикулярных прямых следует вспомнить отмеченное ранее свойство о проецировании прямого угла (рис. 1.3). Прямой угол, одна сторона которого параллельна плоскости проекций, проецируется в свою натуральную величину. Таким образом, чтобы задать прямой угол на чертеже, надо, чтобы одна сторона этого угла являлась прямой уровня.
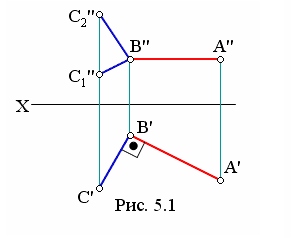
На рис 5.1 угол АВС – прямой, так как сторона АВ (А"В") расположена параллельно горизонтальной плоскости проекций, а на горизонтальной плоскости А'В'С' равен 90°. При этом безразлично как будет направлена сторона ВС на фронтальной плоскости проекций В"С1" или В"С2" , главное, чтобы проекция точки С" находилась на линии связи с С'.
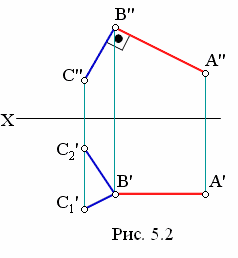
На рис. 5.2 угол АВС так же прямой, отличие лишь в том, что здесь АВ расположена параллельно фронтальной плоскости.
5.1.2. Взаимно перпендикулярные прямая и плоскость
Из курса геометрии средней школы известно, что прямая будет перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым, принадлежащим этой плоскости. Таким образом, чтобы задать прямую n (в дальнейшем будем называть эту прямую нормалью) перпендикулярно к плоскости АВС (рис. 5.3), надо, чтобы она образовала углы 90° с двумя сторонами треугольника АВС. Однако, на чертеже мы не имеем возможности решить эту задачу для любых двух сторон треугольника, так как они являются отрезками общего положения. Здесь уместно вспомнить о главных линиях плоскости – горизонталях и фронталях (см. рис.1.25) и (рис. 1.26).
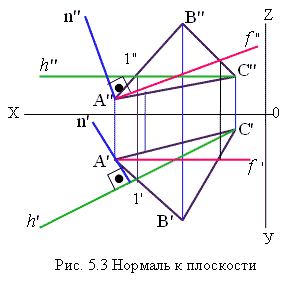
На рис. 5.3 задана прямая n перпендикулярно к горизонтальной проекции горизонтали и перпендикулярно к фронтальной проекции фронтали. Таким образом выполнено условие взаимной перпендикулярности прямой n к двум прямым принадлежащим плоскости АВС, следовательно, мы задали прямую перпендикулярно к плоскости АВС.
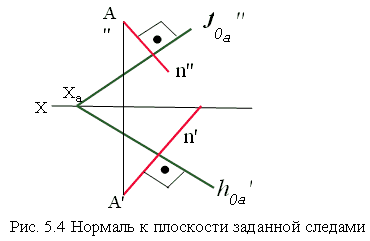
На рис. 5.4 построена нормаль к плоскости заданной следами.
5.1.3. Взаимно перпендикулярные плоскости
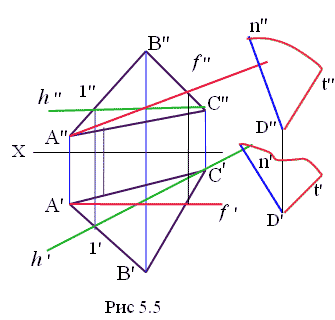
Две плоскости будут взаимно перпендикулярны, если одна из них содержит прямую, перпендикулярную к другой плоскости. Таким образом, чтобы задать плоскость перпендикулярно заданной, надо задать нормаль к этой плоскости и заключить эту нормаль в какую либо плоскость, предварительно продумав способ ее задания (двумя пересекающимися прямыми, прямой и точкой, двумя параллельными прямыми или следами).
Пример: Через точку D задать плоскость перпендикулярно к плоскости АВС. На рис. 5.5 задана плоскостьАВС общего положения и точка D не принадлежащая плоскости. Чтобы задать плоскость через точку Dперпендикулярно к плоскости АВС можно через точку D задать нормаль n к плоскости АВС. Затем можно задать любую прямую пересекающую нормаль, например t (t" t'), в том числе и через точку D.
