1.3. Задание плоскости на чертеже

Плоскость в пространстве может быть задана: тремя точками, не лежащими на одной прямой; прямой и точкой вне ее; двумя пересекающимися прямыми; двумя параллельными прямыми; следами.

1.3.1. Плоскости общего и частного положения. Следы плоскости.

На рис. 1.17 все точки плоскости расположены на разной высоте, разной глубине, удалены от профильной плоскости проекций на разное расстояние и проекции точек не принадлежат одной прямой – такие плоскости не параллельны и не перпендикулярны ни к одной из плоскостей проекций и называются плоскостями общего положения.

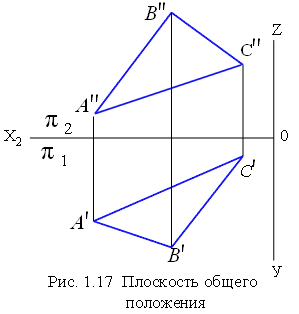
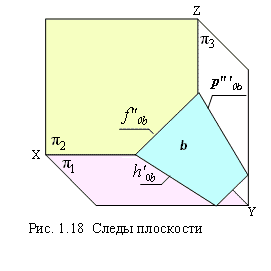
Следами называются прямые, по которым исследуемая плоскость пересекается с плоскостями проекций. На рис. 1.18 плоскость β пересекается с горизонтальной плоскостью π₁ по прямой h_ob', которая является горизонтальным следом плоскости. По существу эта прямая является горизонталью нулевого уровня, именно так она и обозначается. Прямые f_ob'' и p_ob''' -соответственно фронтальный и профильный следы плоскости. На рис 1.19 изображен чертеж плоскости, заданной следами.

 

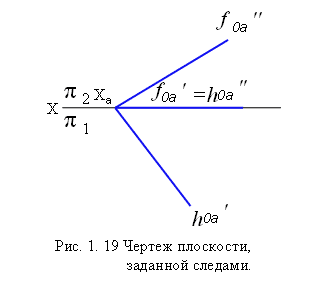
При решении задач горизонтальную проекцию фронтального следа f_oa' и фронтальную проекцию горизонтального следа h_oa'', которые совпадают с осью Х, не изображают. Х_a- точка схода следов плоскости.

В пространстве плоскости могут занимать различное положение относительно плоскостей проекций.

Плоскости, расположенные параллельно одной из плоскостей проекций, называются плоскостями уровня.

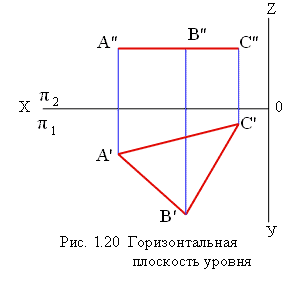
На рис 1.20 изображена плоскость, расположенная параллельно горизонтальной плоскости проекций. Одновременно она перпендикулярна двум другим плоскостям проекций. На ту плоскость проекций, параллельно которой расположены плоскости уровня, они проецируются без искажений, то есть в свою натуральную величину (Н.В.)

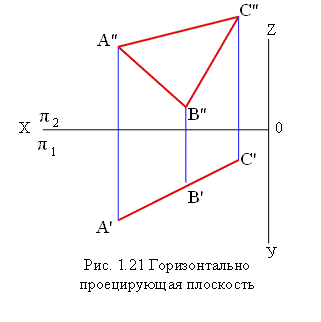
Плоскости, расположенные перпендикулярно к одной из плоскостей проекций, называются проецирующими. На рис. 1.21 представлена горизонтально проецирующая плоскость.  На горизонтальную плоскость проекций она проецируется в прямую линию.

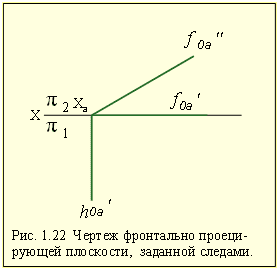
На рис. 1.22 изображена фронтально проецирующая плоскость, заданная следами.

 

1.3.2. Принадлежность прямой и точки к плоскости.

Прямая однозначно задается двумя точками, следовательно, для того, чтобы она принадлежала плоскости, надо чтобы две любые точки этой прямой одновременно принадлежали плоскости.

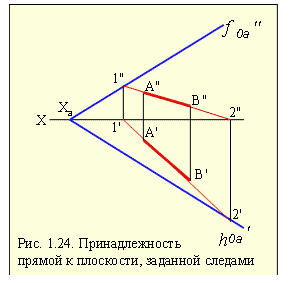
На рис. 1.23 прямая g принадлежит плоскости АВС, так как она проходит через точки 1 и С принадлежащие плоскости. На рис. 1.24 представлена прямая АВ принадлежащая плоскости, заданной следами, так как она проходит через точки 1 и 2, принадлежащие плоскости.

Точка D (рис.1.23) принадлежит плоскости АВС, так как она принадлежит прямой g, принадлежащей этой плоскости.

 

1.3.3. Главные линии плоскости.

Среди множества прямых линий, которые могут принадлежать исследуемым плоскостям, особое место занимают следующие.

1. Горизонтали h

2. Фронтали f 

3. Профильные прямые p

4. Линии наибольшего ската t

 

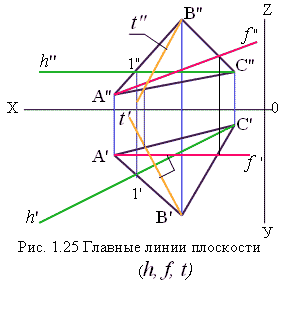
На рис. 1.25 прямая h принадлежит плоскости АВС и является ее горизонталью. Прямая f также принадлежит АВС и является ее фронталью.

Линиями наибольшего ската называются прямые, принадлежащие исследуемой плоскости и расположенные перпендикулярно к горизонталям или фронталям. На рис. 1.25 t принадлежит плоскостиАВС, так как проходит через точку В и точку на отрезке АС и расположена перпендикулярно к проекции горизонтали  h' (см. рис. 1.3). ). На основании этого угол между t и h -прямой. Взаимное положение прямой и плоскости см. [2, стр. 39]

Теперь вы должны выполнить задачи 5 и 6 контрольной работы

Практическое занятие 3.   Задание плоскости на чертеже

Для задания плоскости тремя точками, достаточно задать их проекции (см. практическое занятие 1, «задание точки»).

Для построения следов этой плоскости, необходимо найти горизонтальные следы двух любых отрезков этой плоскости и один фронтальный (или наоборот, два фронтальных и один горизонтальный). Через горизонтальные следы отрезков провести прямую до пересечения с осью Х. Эта прямая является горизонтальным следом. Точка пересечения горизонтального следа с осью Х, является точкой схода следов. Через точку схода следов и ранее построенный один фронтальный след отрезка, задать прямую, которая является фронтальным следом этой плоскости. Нахождение следов отрезков см. следы прямой.

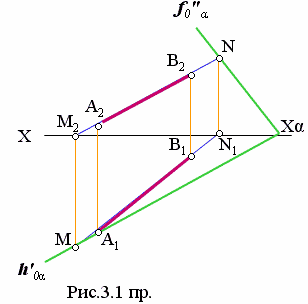
Чтобы заключить отрезок в плоскость, необходимо выполнить следующее. На рис. 3.1 задан отрезок АВ (А₁ В₁ , А ₂ В ₂ ). Находим следы этого отрезка: М – горизонтальный след; N – фронтальный. В любом месте на оси Х назначаем точку схода следов – Хα (плоскость обозначим как α). Из точки схода следов(Хα) через фронтальный след отрезка (N) проводим прямую, которая является фронтальным следом плоскости – f"_oα. Аналогично, из точки схода следов (Хα) через горизонтальный след отрезка (М) – задаем горизонтальный след плоскости.

По данной теме Вам необходимо выполнить в контрольной работе задачи №6 и №5.

Тема 2