5.1.8. Определение расстояний между скрещивающимися прямыми

Наиболее простой путь решения подобных задач сводится к преобразованию чертежа так, чтобы одна из прямых общего положения стала проецирующей (см. рис. 2.1).

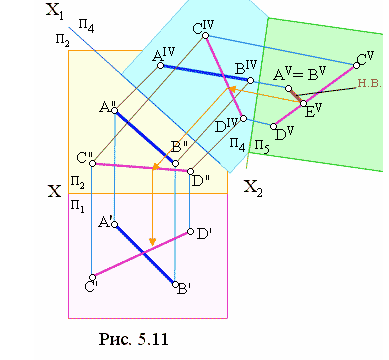
На рис. 5.11 Заданы скрещивающиеся прямые АВ и CD. Для определения расстояния между ними преобразуем АВ в проецирующую прямую, предварительно преобразовав ее в прямую уровня. На чертеже: Вводим дополнительную плоскость проекций п₄ и располагаем ее перпендикулярно к п₂. Задаем новую ось Х₁ параллельно А"В". Согласно алгоритму замены плоскостей (см. подраздел 2.1) на плоскостип₄ построим проекции A^IVB^IVC^IVD^IV. Затем вводим еще одну дополнительную плоскость проекций п₅ и располагаем ее перпендикулярно к п₄ и перпендикулярно к АВ (А^IV B^IV). В новой системе А^VВ^Vотобразилась в точку. Из совпадающих точек А ^VВ^V опустим перпендикуляр на СD (C^V D^V ). Построенный перпендикуляр является кратчайшим расстоянием между данными скрещивающимися прямыми. Возврат построений осуществляется по стрелкам показанным из проекции точки Е^V.

5.2. Определение углов

При рассмотрении свойств параллельного проецирования следует отметить следующее. Любая плоская фигура, расположенная параллельно плоскости проекций, проецируется на нее без искажения, то есть, в свою натуральную величину. Отсюда следует, что любой плоский угол, стороны которого расположены параллельно плоскости проекций, так же проецируется без искажения. Это обстоятельство и положено в основу определения натуральной величины углов.

5.2.1. Определение углов между двумя пересекающимися прямыми

Две пересекающиеся прямые образуют плоскость, отсюда, определить углы можно двумя способами: способом замены плоскостей (плоскость общего положения преобразовать в плоскость уровня - см. рис. 2.2) и способом вращения вокруг осей, расположенных параллельно плоскости проекций (см. рис. 2.4).

5.2.2. Определение углов между двумя скрещивающимися прямыми

Углом между скрещивающимися прямыми называется плоский угол, который образуется между прямыми, проведенными из произвольной точки пространства параллельно данным скрещивающимся прямым.

 

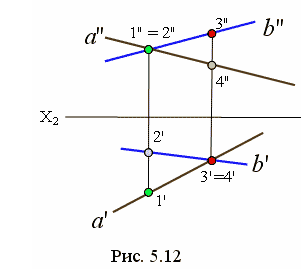
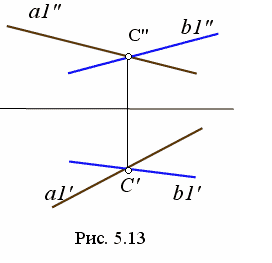
На рис. 5.12 представлены две скрещивающиеся прямые a и b. Чтобы определить угол между этими прямыми надо задать две пересекающиеся прямые. На рис. 5.13 прямая a1 пересекается с прямой b1, в точке С. При этом a1 параллельна a; b1 параллельна b.

5.2.3. Определение углов между прямой общего положения и плоскостью общего положения

Угол между прямой и плоскостью определяется как острый угол между этой прямой и ее проекцией на данную плоскость.

 

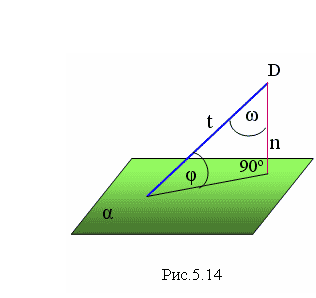
На рис. 5.14 острый угол φ между прямой t и плоскостью α может быть найден с помощью дополнительного угла ω. Для этого надо из любой точки прямой t (на рис.5.14 это точка D) опустить перпендикуляр n на заданную плоскость. Тогда искомый угол определится как φ = 90º - ω.

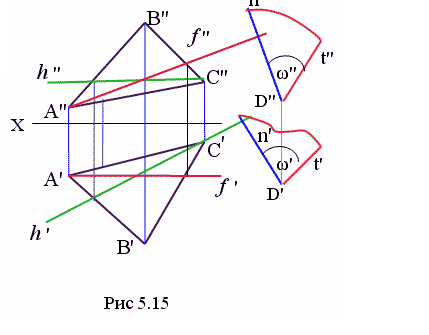
На рис. 5.15 Задана плоскость общего положения АВС и прямая t. Из точки D проведена нормаль к плоскости АВС. Требуется определить угол ω. Для этого надо воспользоваться рассмотренными ранее способом замены плоскостей проекций (см. рис. 2.2) или способом вращения вокруг осей, расположенных параллельно плоскости проекций (см. рис. 2.4).