
- •Дорогі друзі!
- •Вступ
- •Розділ 1
- •Фізика як природнича наука. Методи наукового пізнання
- •§ 1. Фізика — наука про природу. Фізичні тіла та фізичні явища
- •§ 2. Початкові відомості про будову речовини. Молекули. Атоми
- •§ 3. Наукові методи вивчення природи
- •Лабораторна робота № 1
- •§ 5. Похибки й оцінювання точності вимірювань
- •Лабораторна робота № 2
- •§ 6. Творці фізичної науки. Внесок українських учених у розвиток фізики
- •Підбиваємо підсумки розділу 1 «Фізика як природнича наука. Методи наукового пізнання»
- •Завдання для самоперевірки до розділу 1 «Фізика як природнича наука. Методи наукового пізнання»
- •Чому в сучасному світі важко загубитись
- •Теми рефератів і повідомлень
- •Теми експериментальних досліджень
- •Розділ 2
- •Механічний рух
- •§ 8. Матеріальна точка. Траєкторія руху. Шлях. Переміщення
- •§ 9. Рівномірний рух. Швидкість руху
- •§ 10. Графіки рівномірного руху
- •§ 12. Нерівномірний рух. Середня швидкість нерівномірного руху
- •§ 13. Рівномірний рух матеріальної точки по колу. Період обертання
- •§ 14. Швидкість рівномірного руху по колу
- •Лабораторна робота № 4
- •Лабораторна робота № 5
- •Завдання для самоперевірки до розділу 2 «Механічний рух»
- •Космодром в океані
- •Теми рефератів і повідомлень
- •Теми експериментальних досліджень
- •Розділ 3
- •Взаємодія тіл. Сила
- •ЧАСТИНА І. СИЛА. ВИДИ СИЛ
- •§ 16. Явище інерції
- •§ 17. Інертність тіла. Маса як міра інертності
- •Лабораторна робота № 6
- •§ 18. Густина. Одиниці густини
- •Лабораторна робота № 7
- •§ 19. Учимося розв’язувати задачі
- •§ 20. Сила — міра взаємодії. Графічне зображення сил. Додавання сил
- •§ 21. Деформація тіла. Види деформації
- •§ 22. Сила пружності. Закон гука
- •Лабораторна робота № 8
- •§ 23. Сила тяжіння. Вага тіла. Невагомість
- •§ 24. Тертя. Сили тертя
- •Лабораторна робота № 9
- •Завдання для самоперевірки до розділу 3. «Взаємодія тіл. Сила». Частина 1. Сила. Види сил
- •§ 25. Тиск твердих тіл на поверхню. Сила тиску
- •§ 26. Тиск газів і рідин. Закон паскаля
- •§ 27. Гідростатичний тиск
- •§ 28. Атмосферний тиск і його вимірювання. Барометри
- •§ 30. Гідравлічні машини. Насоси
- •§ 31. Виштовхувальна сила в рідинах і газах. Закон Архімеда
- •§ 32. Умови плавання тіл
- •Лабораторна робота № 10
- •§ 33. Судноплавство та повітроплавання
- •Завдання для самоперевірки до розділу 3 «Взаємодія тіл. Сила»
- •Підбиваємо підсумки розділу 3 «Взаємодія тіл. Сила»
- •Навіщо нирцю повітряна куля
- •Теми рефератів і повідомлень
- •Теми експериментальних досліджень
- •Розділ 4
- •Механічна робота та енергія
- •§ 34. Механічна робота. Одиниці роботи
- •§ 35. Потужність
- •§ 36. Енергія. Потенціальна енергія тіла
- •§ 37. Кінетична енергія тіла. Повна механічна енергія
- •§ 38. Закон збереження і перетворення механічної енергії
- •§ 39. Момент сили. Умови рівноваги важеля
- •Лабораторна робота № 11
- •§ 40. Рухомий і нерухомий блоки
- •§ 41. Прості механізми. «Золоте правило» механіки
- •§ 42. Коефіцієнт корисної дії механізмів
- •Лабораторна робота № 12
- •Завдання для самоперевірки до розділу 4 «Механічна робота та енергія»
- •Навіщо свідомо знищувати автомобілі
- •Відповіді до вправ та завдань для самоперевірки
- •Алфавітний покажчик
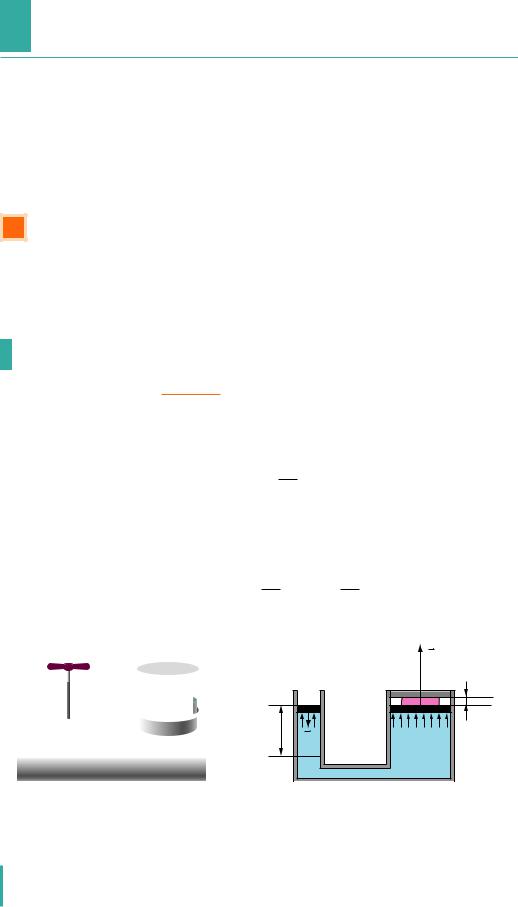
Розділ 3. Взаємодія тіл. Сила. Частина ІІ
§ 30. ГІДРАВЛІЧНІ МАШИНИ. НАСОСИ
Чи може людина підняти слона, маючи тільки з’єднані між собою циліндри з поршнями та невелику кількість рідини? На перший погляд — ні. Але автолюбителі за допомогою невеликого пристрою — гідравлічного домкрата — піднімають свій автомобіль для заміни колеса або для ремонту, a на заводах працюють гідравлічні преси, які штампують деталі машин із металевих заготівок. Як можна, прикладаючи меншу силу, отримувати більшу, ви дізнаєтесь із цього параграфа.
1 |
Використовуємо гідравлічний прес для отримання виграшу в силі |
Як ви вже добре знаєте, тиск, створюваний на поверхню нерухомої |
|
рідини, передається рідиною однаково в усіх напрямках (закон Паскаля). |
|
Цю властивість рідин широко використовують у гідравлічних машинах. |
|
Розгляньмо принцип дії деяких із них на прикладі гідравлічного преса, |
|
який застосовують для пресування фанери та картону, для віджимання |
|
олії, для виготовлення деталей машин і механізмів тощо. |
|
Гідравлічний прес — це найпростіша гідравлічна машина, яка використовується для створення великих сил стиснення.
Гідравлічний прес (рис. 30.1) складається з двох сполучених циліндрів різного діаметра, які заповнені робочою рідиною (частіше машинним мастилом) і закриті рухомими поршнями.
Якщо до поршня меншого циліндра прикласти силу F1 (рис. 30.1, б), то ця сила створить на поверхню рідини певний додатковий тиск p:
p = F1 ,
S1
де S1 — площа меншого поршня.
Відповідно до закону Паскаля, цей тиск передаватиметься в усі точки
рідини, що заповнює сполучені циліндри. Отже, рідина почне тиснути на |
|||||
поршень більшого циліндра з певною силою F2: |
|
|
|||
F = pS = |
F1 |
S = F |
S2 |
, |
|
2 |
2 |
S |
2 1 |
S |
|
де S2 — площа більшого поршня. |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
F2 |
|
|
S1 |
S |
h2 |
|
h1 |
|
|
2 |
|
F1 |
|
|
|
|
|
|
|
|
а |
б |
|
|
|
Рис. 30.1. Гідравлічний прес дає можливість отримати виграш у силі: діючи на малий поршень із площею S1 меншою силою F1, маємо змогу стискати (пресувати) тіло, розташоване над поршнем із площею S2, більшою силою F2
188
|
|
|
|
|
§ 30. Гідравлічні машини. Насоси |
||
|
Сила, що діє з боку рідини на великий по- |
|
|
||||
|
ршень, є більшою від сили, що діє на малий |
|
|
||||
|
поршень, у стільки разів, у скільки разів пло- |
|
g |
||||
|
ща великого поршня більша від площі малого: |
||||||
|
g |
F |
|||||
|
|
F2 |
S2 |
|
F1 |
2 |
|
|
|
|
Нагнітаючий |
Поршень |
|||
|
|
F1 |
= S1 |
|
поршень |
підйомника |
|
|
Відношення |
F2 |
— це виграш у силі. |
S1 |
S |
||
|
|
F1 |
|
|
Клапани |
2 |
|
|
|
|
|
|
|||
|
Гідравлічний |
прес дозволяє |
одержати |
Кран |
|||
|
|
|
|||||
значний виграш у силі, який залежить від |
|
|
|||||
відношення площ поршнів: чим більше різ- |
|
|
|||||
нитимуться між собою площі поршнів, тим |
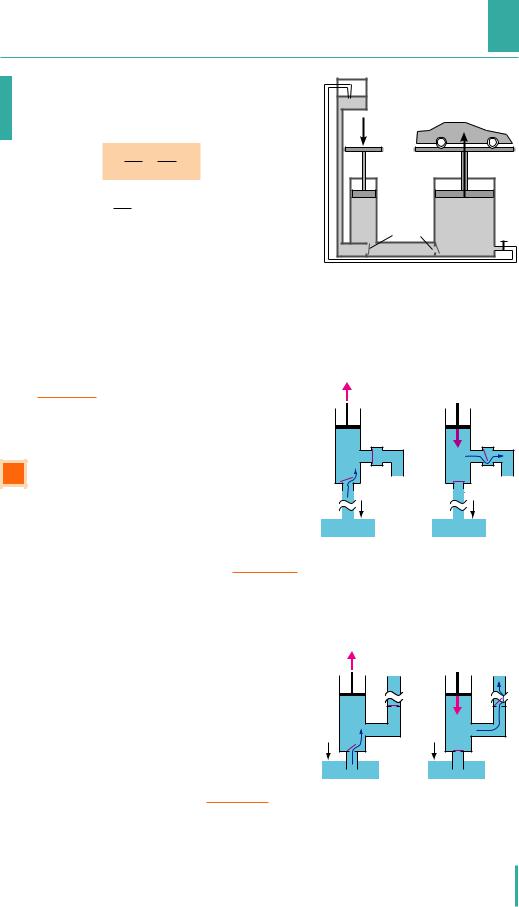
Рис. 30.2. Гідравлічний підйомник — |
||||||
більший виграш у силі матимемо. |
приклад гідравлічної машини |
||||||
|
За таким принципом працюють і інші |
|
|
||||
гідравлічні інструменти та пристрої. Так, |
|
|
|||||
гідравлічний підйомник дозволяє, приклав- |
|
|
|||||
ши невелику силу, підняти важкий автомо- |
|
|
|||||
біль (рис. 30.2). |
|
|
|
|
|
||
|
Спробуйте, скориставшись рис. 30.2, са- |
|
|
||||
мостійно розібратися, як працює такий під- |
|
|
|||||
йомник. |
|
|
|
b |
b |
||
2 |
Використовуємо насоси для |
a |
a |
||||
відкачування води |
|
|
|||||
|
|
pа |
pа |
||||
Найпершими гідравлічними машинами, які |
|||||||
|
|
||||||
застосовували ще в стародавні часи, були |
|
|
|||||
всмоктувальні |
та |
нагнітальні |
поршневі |
|
|
||
насоси. |
|
|
|
Рис. 30.3. Принцип дії всмоктуваль- |
|||
|
У всмоктувальному насосі |
(рис. 30.3) |
|||||
внаслідок підняття поршня тиск у резер- |
ного насоса: вода піднімається за |
||||||
поршнем унаслідок дії сили атмосфер- |
|||||||
вуарі під поршнем зменшується і клапан |
ного тиску |
|
|||||
а відкривається. Через цей відкритий кла- |
|
||||||
пан вода під впливом атмосферного тиску |
|
|
|||||
pа |
піднімається в резервуар під поршнем. |
|
|
||||
Коли поршень почне рухатися вниз, клапан |
|
|
|||||
а закриється, а клапан b відкриється, і вода |
с |
с |
|||||
виливатиметься через кран насоса. У разі |
|||||||
b |
b |
||||||
дальшого руху поршня вгору все повторю- |
|||||||
ється. Максимальна висота, на яку можна |
pа a |
pа a |
|||||
підняти воду за допомогою всмоктувального |
|
|
|||||
насоса, визначається атмосферним тиском |
|
|
|||||
і становить 10,3 м (пригадайте чому). |
|
|
|||||
|
У нагнітальному насосі (рис. 30.4) під |
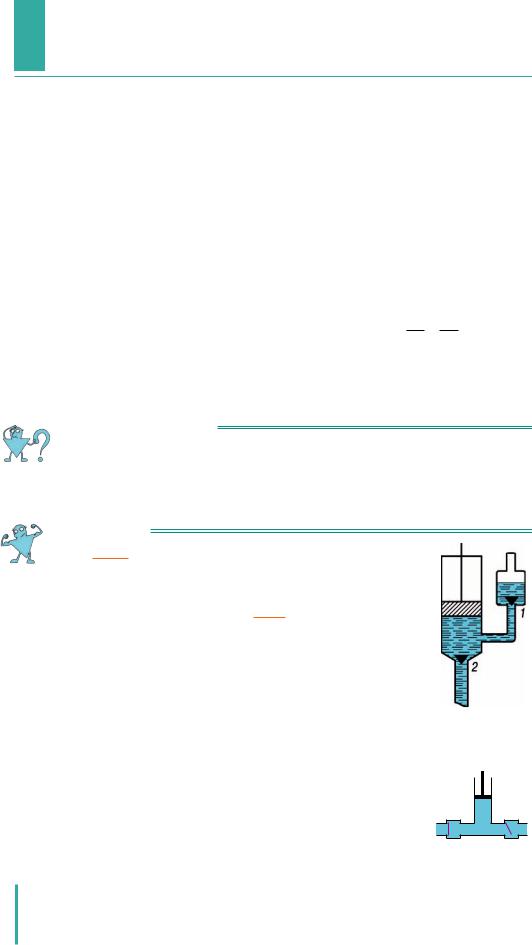
Рис. 30.4. У нагнітальному насосі |
|||||
час руху поршня вгору тиск над поверх- |
|||||||
всмоктування води під час кожного |
|||||||
нею рідини над клапаном a і під клапаном |
зворотного руху поршня змінюється |
||||||
b зменшується. |
Унаслідок цього клапан a |
нагнітанням води в трубу водогону |
|||||
|
|
|
|
|
|
189 |
|
Розділ 3. Взаємодія тіл. Сила. Частина ІІ
відкривається, а клапан b — закривається. Під дією сили атмосферного тиску pа вода піднімається за поршнем через відкритий клапан a. Потім, коли поршень почне рухатися вниз, через збільшення тиску під поршнем клапан a закриється, а клапан b відкриється. Поршень витисне через клапан b воду у вертикальну трубу c. Під час наступного руху поршня вгору клапан b буде закритий і вода з вертикальної труби c не потраплятиме назад у насос.
 Підбиваємо підсумки
Підбиваємо підсумки
Властивість рідини передавати тиск, створюваний на її поверхню, однаково в усіх напрямках покладена в основу дії гідравлічних машин і насосів.
Сила, що діє з боку рідини на великий поршень гідравлічної машини, є більшою від сили, що діє на малий поршень, у стільки разів, у скільки
разів площа великого поршня більша від площі малого: F2 = S2 .
F1 S1
Насоси бувають всмоктувальні та нагнітальні. Неодмінними деталями насосів є поршень, циліндр та клапани, що пропускають рідину тільки в одному напрямку.
Контрольні запитання
1. На якому законі ґрунтується дія гідравлічної машини? 2. Що таке гідравлічний прес і де його застосовують? 3. Сформулюйте умову рівноваги поршнів гідравліч ної машини. 4. Де застосовують насоси? 5. Які види поршневих насосів ви знаєте? 6. Чим визначається висота підняття рідини у всмоктувальному насосі?
Вправа № 30
1.На рис. 1 зображено схему поршневого насоса. Який це насос: всмоктувальний чи нагнітальний? У якому положенні (відкритому чи закритому) будуть клапани під час руху поршня вниз?
2.Куди рухається поршень насоса (рис. 2): вгору чи вниз?
3.Яке зусилля розвиває гідравлічний прес, якщо до малого поршня прикладають силу 100 Н? Площі поршнів дорівнюють 2 см2 і 12 см2.
4.На більший поршень гідравлічної машини діє сила 4 кН. Яка сила діє на менший поршень, якщо площі поршнів дорівнюють відповідно 400 і 10 см2?
5.Щоб за допомогою гідравлічної машини підняти контейнер вагою 3 кН, до малого поршня прикладають силу 200 Н. Чому дорівнює площа великого поршня, якщо площа малого становить 4 см2?
6.Площа малого поршня гідравлічної машини 15 см2, вели кого — 3 дм2. Визначте масу вантажу, який можна підняти за допомогою цієї машини, приклавши до малого поршня силу 200 Н.
7.Малий поршень гідравлічної машини опустився під дією сили 300 Н на 4 см, а великий піднявся на 1 см. Яка сила діяла на великий поршень?
Рис. 1
Рис. 2
190

§31. Виштовхувальна сила в рідинах і газах. Закон Архімеда
8.Перед вами рисунок моделі гідравлічного преса (рис. 3). Користуючись даними, наведеними на рисунку, визначте:
а) напрямок руху поршня; б) силу, яка діє на великий поршень, якщо
на малий поршень діють із силою 100 Н; в) виграш у силі, що дозволяє одержати цей прес;
г) висоту, на яку підніметься великий
поршень, якщо малий опустити на 10 см. |
Рис. 3 |
9.Cкориставшись додатковою літературою або Інтернетом, дізнайтеся про деякі гідравлічні пристрої, не розглянуті в параграфі (наприклад гідравлічна система гальмування автомобіля, гідравлічні ножиці, різноманітні насоси). Як вони працюють і де їх застосовують? Оформте повідомлення про один із пристроїв.
10.Визначте осадку корабля, що дістав пробоїну в дні, якщо матрос, маса якого 80 кг, зміг перекрити доступ води, накривши отвір пластиною площею 200 см2 і ставши на неї. Масу пластини не враховуйте.
Фізика і техника в Україні
Харківський національний університет (ХНУ) імені В. Н. Каразіна, заснований у листопаді 1804 р.,— один із найстаріших університетів Схід ної Європи. Історія ХНУ є невід’ємною частиною інтелектуальної, культурної та духовної історії України.
З Харківським університетом пов’язані імена таких усесвітньовідомих науковців та просвіти телів, як П. П. Гулак-артемовський, О. М. Ляпунов,
М. І. Костомаров, М. П. Барабашов, М. М. Бекетов, Д. І. Багалій, А. М. Краснов, М. В. Остро градський, В. А. Стеклов, О. О. Потебня, О. В. Погорєлов та багато інших. Харківський уні верситет — єдиний в Україні, де навчались або працювали три лауреати Нобелівської пре мії — біолог І. І. Мечников, економіст Саймон Кузнець, фізик Л. Д. Ландау.
§ 31. Виштовхувальна сила в рідинах і газах. Закон Архімеда
Чому м’яч, який занурили у воду й відпустили, вискакує над поверхнею води? Чому важкий камінь, який на суходолі не можна зрушити з місця, легко підняти під водою? Чи правда, що людина у воді перебуває в стані невагомості? Спробуймо розібратися!
1Доводимо існування виштовхувальної сили
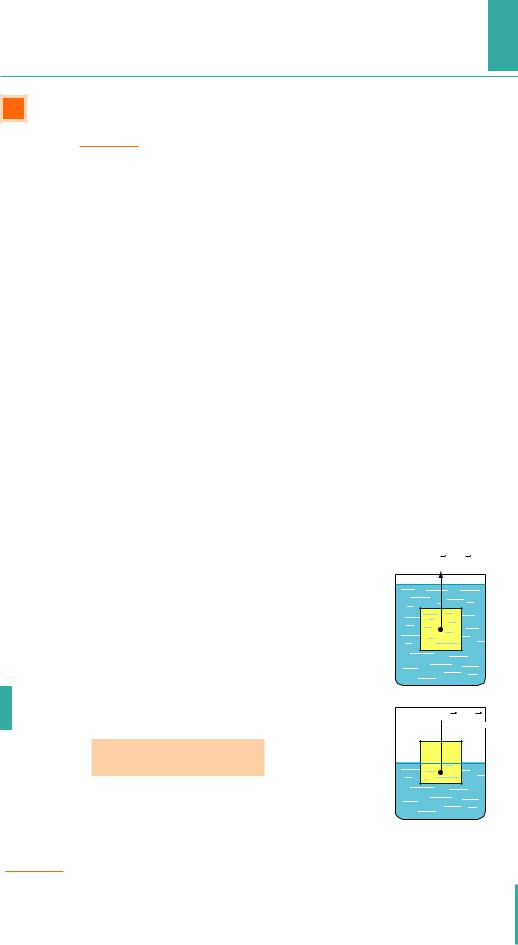
Підвісимо до коромисла терезів дві однакові кулі. Оскільки маси
куль є рівними, терези будуть зрівноважені (рис. 31.1, а). Підставимо під праву кулю порожню посудину (рис. 31.1, б). Наллємо в посудину воду
191

Розділ 3. Взаємодія тіл. Сила. Частина ІІ
а
б
в
Рис. 31.1. На кулю у воді діє сила, напрямлена вгору
F |
h1 |
1 |
|
F3 

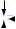
 F4 h2
F4 h2
F2
Рис. 31.2. Сили тиску F3 і F4 , що діють на бічні грані кубика, зрівноважені (F3 = F4 ) .Сила тиску F2 , яка діє на нижню грань кубика, більша за силу тиску F1 , що діє на верхню грань (F2 > F1)
Рис. 31.3. Айсберг плаває на по верхні води завдяки дії виштовху вальної (архімедової) сили
і побачимо, що рівновага терезів порушиться (рис. 31.1, в) — якась сила намагається виштовхнути кулю з води.
Звідки ж береться ця сила? Щоб розібратися, розгляньмо занурений у рідину кубик. На нього з усіх боків діють сили гідростатичного тиску рідини (рис. 31.2).
Сили гідростатичного тиску F3 і F4 , що діють на бічні грані кубика, є протилежними за напрямком і рівними за значенням: площі бічних граней однакові, і грані розташовані на однаковій глибині. Такі сили зрівноважують одна одну.
А от сили гідростатичного тиску F1 і F2 , що відповідно діють на верхню і нижню грані кубика, одна одну не зрівноважують.
На верхню грань кубика діє сила тиску F1 :
F1 = p1S = ρрідgh1 S ,
де p1 = ρрідgh1 — гідростатичний тиск рідини,
ρрід — густина рідини, h1 — глибина занурення верхньої грані кубика, S — площа грані.
Аналогічно на нижню грань кубика діє сила тиску F2 :
F2 = ρрідgh2S .
Нижня грань перебуває на більшій глибині, ніж верхня (h2 > h1 ) , тому сила тиску F2 більша за силу тиску F1 . Рівнодійна цих сил дорівнює різниці значень сил F2 і F1 і напрямлена в бік дії більшої сили, тобто вертикально вгору.
По вертикалі вгору на кубик, занурений у рідину, діє сила, зумовлена різницею тисків на його нижню і верхню грані,— виштовхувальна сила:
Fвишт = F2 − F1.
На тіло, розташоване в газі, також діє виштовхувальна сила, але вона значно менша за силу, що діє на це тіло в рідині, адже густина газу набагато менша за густину рідини.
Виштовхувальну силу, яка діє на тіло в рідині (рис. 31.3) або в газі, називають також архімедовою силою (на честь давньогрецького вченого Архімеда, який уперше вказав на її існування та обчислив її значення).
192
§ 31. Виштовхувальна сила в рідинах і газах. Закон Архімеда
2 |
Розраховуємо архімедову силу |
|
Обчислимо значення архімедової сили для кубика, зануреного в рі- |
||
|
||
дину (див. рис. 31.2). |
||
|
Ми вже показали, що архімедова (виштовхувальна) сила дорівнює різни- |
|
ці сил тисків рідини на нижню і верхню грані кубика (див. п. 1): |
||
Fарх = F2 − F1,
де F1 = ρрідgh1S — сила тиску рідини на верхню грань кубика,
аF2 = ρрідgh2S — сила тиску рідини на нижню грань кубика. Знаючи F2 і F1 , знайдемо виштовхувальну силу:
Fарх = ρрідgh2S − ρрідgh1S = ρрідgS(h2 − h1 ).
Різниця глибин h2 −h1 , на яких перебувають нижня і верхня грані кубика, є висотою h кубика, отже, Fарх = ρрідgS h .
Добуток площі S основи кубика на його висоту h — це об’єм V кубика: V =Sh, тож маємо формулу для розрахунку архімедової сили:
Fарх = ρрідgV .
Легко побачити, що ρрідV — це маса рідини в об’ємі кубика (mрід ), отже,
Fарх =mрідg = Pрід.
Архімедова сила дорівнює вазі рідини в об’ємі ку-
бика: Pрід = Fарх .
Наші міркування ми проводили для кубика, який був повністю занурений у рідину. Але отриманий результат справджується і для тіла будь-якої форми, і для випадків, коли тіло занурене в рідину частково,— для розрахунків лише потрібно брати
об’єм зануреної в рідину частини тіла. Крім того, результат справджується й для газів.
А тепер сформулюємо закон Архімеда:
На тіло, занурене в рідину або газ, діє виштовхуваль на сила, яка дорівнює вазі рідини або газу в об’ємі зануреної частини тіла:
Fарх = ρрід (газу)gVзан
Тут Fарх — архімедова сила, ρрід (газу) — густина рідини або газу, Vзан — об’єм зануреної частини тіла.
Сила Архімеда прикладена до центра зануреної частини тіла і напрямлена вертикально вгору (рис. 31.4).
F х (Fвишт )
 Fарх (Fвишт )
Fарх (Fвишт )
Рис. 31.4. Точка прикла дання та напрямок сили Архімеда
193

Розділ 3. Взаємодія тіл. Сила. Частина ІІ
3З’ясовуємо, що ніякої втрати ваги тіла в рідині немає
Підвісимо до динамометра камінець на нитці. Динамометр покаже
вагу камінця. Підставимо склянку з водою так, щоб камінець був повністю занурений у воду. Показ динамометра зменшиться. Здається, що камінець «утратив» частину своєї ваги. Але ніякої втрати ваги тіла в рідині не відбувається: вага перерозподіляється між підвісом (ниткою) і опорою (рідиною). Навіть якщо архімедова сила, що діє на тіло, є достатньою, щоб утримати це тіло, і підвіс не буде розтягнутий, то тіло все одно не перебуває в невагомості, адже воно тисне на опору — рідину.
Однак треба зазначити: коли тіло плаває, його вага розподіляється на воду, що оточує всю поверхню тіла. Тому під час плавання у воді нам здається, що ми втратили вагу. Такі комфортні умови підтримування важкого тіла зумовили те, що внаслідок еволюції наймасивніші істоти на Землі мешкають в океані: найбільшою твариною на нашій планеті є кит, маса якого може сягати 150 т, а довжина — 35 м.
Саме архімедова сила допомагає нам піднімати у воді важкі камені або інші предмети, адже частина сили тяжіння, що діє на ці тіла, зрівноважується не силою наших рук, а архімедовою силою.
Однак є випадки, коли вода не допомагає підняти тіло, а навпаки — заважає. Це трапляється, коли тіло лежить на дні й щільно до нього прилягає. Вода не може потрапити під нижню поверхню тіла і допомогти своїм тиском підняти його. Щоб відірвати тіло від дна, слід подолати силу тяжіння, яка діє на тіло, а також силу тиску води на верхню поверхню тіла. (До речі, саме з цим ми маємо справу, коли намагаємося витягти пробку з наповненої водою ванни.) Слід зауважити, що зазначене явище може призвести й до трагедії: якщо підводний човен опуститься на глинисте дно і витіснить із-під себе воду, самотужки спливти він не зможе.
4Учимося розв’язувати задачі
Задача. Суцільний алюмінієвий брусок масою 540 г повністю зану-
рений у воду і не торкається дна та стінок посудини. Знайдіть архімедову силу, що діє на брусок.
Дано: |
|
|
|
|
|
|
|
|
|
Аналіз фізичної проблеми. |
|||||||||||||
m =540 г =0,54 кг |
На занурений у воду алюмінієвий брусок діє архі- |
||||||||||||||||||||||
ρ |
|
= 2700 |
кг |
|
|
|
|
медова сила. Для її обчислення потрібно знати гус- |
|||||||||||||||
|
|
|
|
|
тину води та знайти об’єм бруска. Для визначення |
||||||||||||||||||
ал |
м3 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
об’єму бруска скористаємось визначенням густини |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
кг |
|
|
|
|||||||||||||
ρводи |
= 1000 |
|
|
|
тіла: ρ |
|
|
= |
m |
. Густини води та алюмінію знайдемо |
|||||||||||||
м3 |
|
|
|
ал |
|||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|||||
g = 9,8 |
Н |
≈10 |
|
Н |
в таблиці. |
б |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
Пошук математичної моделі, розв’язання. |
|||||||||||||||||||
|
|
|
|
кг |
кг |
||||||||||||||||||
|
|
|
|
За законом Архімеда: Fарх = ρводиgVб . |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Fарх — ? |
|
|
|
||||||||||||||||||||
|
|
|
Об’єм бруска знайдемо з визначення густини: |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
= |
m |
|
V = |
m |
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
ал |
V |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
ρ |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
ал |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
194
§ 31. Виштовхувальна сила в рідинах і газах. Закон Архімеда
Підставимо вираз для об’єму бруска у формулу для розрахунку архі-
медової сили: F = |
ρводиgm |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
арх |
ρал |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кг |
|
|
Н |
кг |
|||||
|
|
|
|
F |
|
|
|
м3 |
|
кг |
||||||
Перевіримо одиницю шуканої величини: |
= |
|
|
|
|
= Н . |
||||||||||
|
|
|
кг |
|
|
|||||||||||
|
|
|
|
арх |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
м3 |
|
|
||
Знайдемо числове значення: F = |
1000 10 0,54 |
|
= 2 (Н). |
|
|
|||||||||||
|
|
|
|
|||||||||||||
|
|
арх |
2700 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Відповідь: на алюмінієвий брусок діє архімедова сила 2 Н.
 Підбиваємо підсумки
Підбиваємо підсумки
На тіло, що перебуває в рідині або газі, діє виштовхувальна (архімедова) сила. Причина її появи в тому, що гідростатичні тиски рідини або газу, які діють на верхню і нижню поверхні тіла, є різними.
Закон Архімеда: на тіло, занурене в рідину або газ, діє виштовхувальна сила, яка напрямлена вертикально вгору та дорівнює вазі рідини або газу в об’ємі зануреної частини тіла: Fарх = ρgVзан.
Контрольні запитання
1.Куди напрямлена сила, яка діє з боку рідини або газу на тіло, що в них занурене?
2.Що є причиною виникнення виштовхувальної сили? 3. Як іще називають виштов хувальну силу? 4. Сформулюйте закон Архімеда. 5. Чи втрачає вагу тіло, занурене
врідину або газ? Чому? 6. У яких випадках на тіло, занурене в рідину, не діє ви штовхувальна сила? Чому?
Вправа № 31
1.Порівняйте виштовхувальні сили, що діють на кульки в таких випадках: а) однакові залізні кульки в посудині з водою (див. рисунок а); б) однакові залізні кульки в посудинах із різною рідиною (див. рисунок б);
в) різні за розміром залізні кульки в посудині з водою (див. рисунок в); г) однакові за розміром кульки з різних матеріалів у посудині з водою (див. рисунок г).
2.Щоб відірвати підводний човен від глинистого дна, водолази прокопують під ним тунелі. Для чого вони це роблять?
3.Сталева куля об’ємом 400 см3 занурена в гас. Обчисліть архімедову силу, що діє на кулю.
4.На кулю, повністю занурену у ртуть, діє архімедова сила 136 Н. Обчисліть об’єм кулі.
5.Алюмінієвий брусок масою 2,7 кг частково занурений у воду. На брусок діє архімедова сила 2,5 Н. Яка частина бруска занурена у воду?
1 |
|
|
|
1 |
|
|
1 |
2 |
3 |
|
2 |
1 |
2 |
3 |
2 |
3 |
|||||
|
||||||||||
|
|
|
|
|
|
|
|
|
||
3 |
олія |
вода |
гас |
|
|
|
|
|
|
|
а |
|
б |
|
|
|
в |
|
г |
|
195
