Лекція №4. Кардинальні числа.

1. Означення кардинального числа (потужності множини).

Означення. Множини X і Y називаються еквівалентними ( X~Y ) якщо існує бієкція , (тобтоспівставляється елементуY, причому різним х співставленні різні у і кожен уY співставленний деякому хєX).

Введене відношення є відношенням еквівалентності (воно задовольняє умовам рефлексивності, симетричності і транзитивності).

Теорема. Нехай при кожному n множини B_n еквівалентні множинам A_n тоді .

Доведення. З метою спрощення сприйняття доведення будемо припускати, що множина B_n та A_n попарно не перетинаються.

Нехай - бієкція і B_n →A_n, тоді , якщобуде бієкцією:. Тобто В~А.

Відношення еквівалентності розбиває сукупність усіх множин на класи еквівалентності. Множини одного класу еквівалентності мають однакову кількість елементів (рівнопотужні), а різних класів - різну кількість.

Приклад.

1. Множини точок двох відрізків - рівнопотужні. Взаємно-однозначно співставити елементи цих множин слід так

2. Множини точок півінтервалів - рівнопотужні. Взаємно-однозначно співставлення елементів цих множин відбувається за допомогою функції y=tg x.

Рівнопотужними є множини натуральних чисел і парних натуральних чисел: N~{2n}, n↔2n.

Означення. Клас, якому належить множина X називається потужністю множини X або кардинальним числом множини X(card X).

Множини одного класу мають однакове кардинальне число, а різних класів -різне.

У класі кардинальних чисел існує відношення порядку: якщо - кардинальне число деякої підмножини множини потужності , то .

Іншими словами: cardX cardY.

Подібно відношенню порядку на числовій прямій, введене відношення упорядковує потужності, А саме:

1. card Xcard Yі card Y card Zcard XcardZ.

2. card Xcard Yі card Ycard Xcard X = card Y (Теорема Шредера-Берштейна).

3. x,y(card X < card Y) або (card Y< card X) (теорема Кантoра).

Таким чином, клас кардинальних чисел впорядкований.

2. Теорема про множину як завгодно великої потужності.

Означення. Потужність X менша за потужність Y (card X < card Y), якщо card Xcard Y

і card Xcard Y.

Для будь-якої множини Х. Позначимо P(X)- множину всіх підмножин множини Х.

Теорема (Кантор). Потужність не порожньої множини Х менша потужності множини усіх її підмножин: card X < card P ( X ).

Доведення. Оскільки Р(Х) містить одноелементні підмножини, то card Xcard P(X).Доведемо, що card X card P(X),тобто ХР(Х). Припустимо супротивне - бієкція. Розглянемо

. Оскільки АР(Х),то такий, що (а) =А.

Тоді:

1. якщо (за означеннямА);

2. якщо (за означенням А).

Отримали протиріччя , що й доводить теорему.

Розглянемо найбільш важливі трансфінітні (потужності нескінчених множин) потужності.

3. Зчисленні множини.

Означення. Множина Х називається зчисленною, якщо вона еквівалентна множині натуральних чисел N, тобто card X = card N = а.

Теорема (необхідна і достатня умова зчисленності). Для того, щоб множина А була зчисленною необхідно і достатньо, щоб її елементи можна було представити у вигляді послідовності.

Доведення. Необхідна умова. Нехай card A=a A~N, тобто існує бієкціяДля будь-якого аА існує єдине, тобто елемент а розташуємо на n-му місці у послідовності. Таким чином всі елементи множини А розташуються у послідовності.

Достатня умова. Нехай тоді a_n↔n, тобто , бієкція: A→N. Отже A~N, що і доводить теорему.

Приклад 1. Z~N, оскільки

Розглянемо теореми про властивості зчисленних множин.

Теорема 1. У будь-якій нескінченій множині можна вибрати зчисленну підмножину.

Доведення. Нехай А – нескінченна множина. Візьмемо будь-яке і позначимо а₁. Оскільки А нескінченна, то у множині А\є елементи. Візьмемо будь-який елемент з А\та позначимо його а₂. У множині А\є елементи. Продовжуючи процес отримуємо множину, що й треба довести.

Теорема 2. Об’єднання скінченної або зчисленної множин – зчисленне.

Доведення. Нехай , де card A_i=a, i =1,… . Покажемо, що card A=a, тобто А~N. Оскільки А_і~N то для кожного i =1,… множини А_і можливо представити у вигляді послідовності: , i =1, 2, … .

Множину А можливо представити у вигляді

, тоді , де розташування елементів у порядку зросту суми індексів. Згідно теоремиA~N, що і треба було довести.

Теорема 3. Декартовий добуток скінченого числа зчисленних множин - зчисленний.

Доведення. Нехай А=, де А_і – зчисленні. Доведемо по індукції. Нехай n=2 , де- зчисленна оскільки А₁ – зчисленна. Оскільки А₂ – зчисленна, то - зчисленне об’єднання зчисленних множин – тобто зчисленна множина, згідно з властивістю 2.

Нехай при n=k (А=), А – зчисленна. Доведемо, що при n=k+1 А=- зчисленна. Отже

А=, множина- зчисленна, згідно припущення, а A_k+1 – зчисленна за умовою. Згідно доведення для n=2 добуток - зчисленна множина, що й треба було довести.

Приклад 2 Множина алгебраїчних чисел - зчисленна.

Нехай А – множина алгебраїчних чисел, тоді , де А_n множина коренів многочленів порядку n з раціональними коефіцієнтами. Позначимо - множина коренів многочленна а₀хⁿ+…+a_n (вона скінченна), тоді .

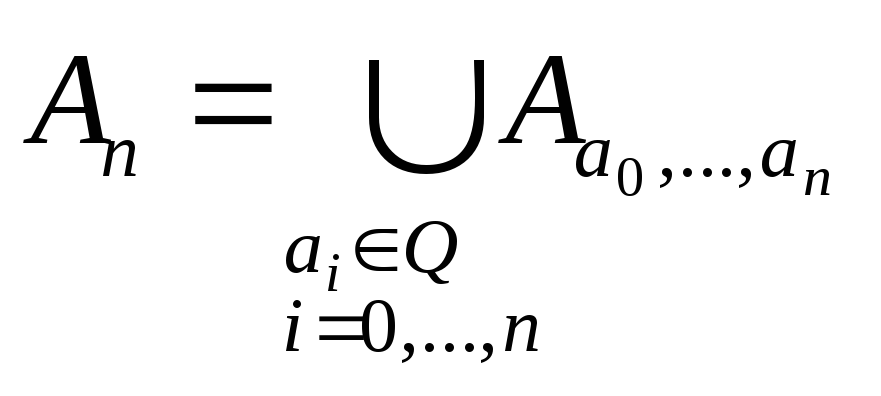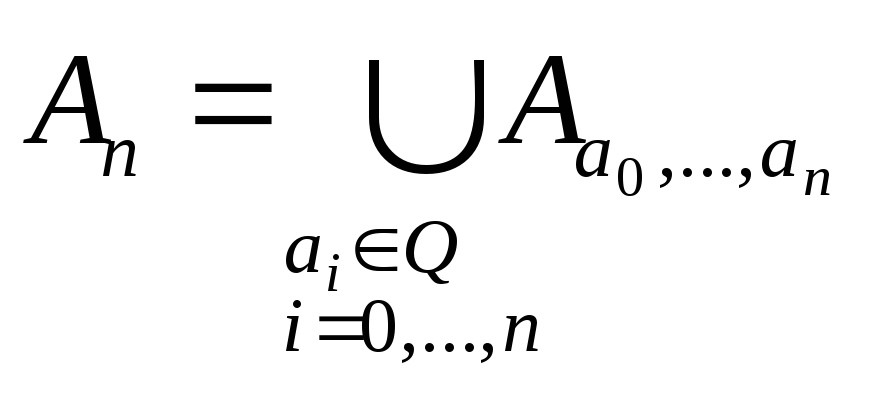Множина наборів (а_0, …, a_n), а_{і, і=0,…n}зчисленна згідно властивості 3, тобто об’єднання - зчисленне об’єднання скінченних множин. Згідно з властивістю 2 А_n – зчисленне, тоді теж зчисленне.

Приклад 3. card Q=a. Дійсно - зчисленна.

Теорема 4. Нехай X- нескінчена множина і card А = а, тоді ХА ~ X.

Доведення. Оскільки Х – нескінченна, то існує зчисленна множина МХ, тоді

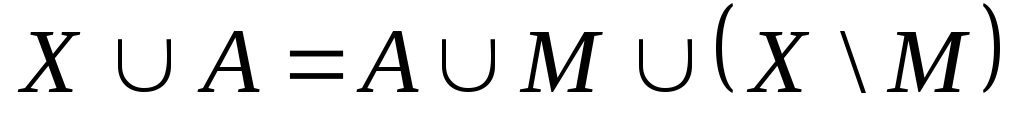(card AM=a)

, тобто .