Операции над комплексными числами

Алгебраическую операцию сложения на множестве можно задать следующим образом:

.

Сложение комплексных чисел ассоциативно, т.е. и коммутативно, т.е.. Сумма чисел, поэтому числоявляется противоположным числу, тем самым определена операция вычитания.

Учитывая, что через обозначен корень уравнения, т.е.или, можно определить умножение комплексных чисел:

.

Умножение также ассоциативно и коммутативно. Произведение нескольких сомножителей вычисляется как последовательное умножение. Натуральная степень комплексного числа может быть найдена при помощи формулы бинома Ньютона. Поскольку,,,,, при возведениив любую натуральную степень, надо найти остаток от деленияна 4 и возвестив степень, равную этому остатку.

Чтобы определить деление комплексных чисел, нужно определить число обратное числу . Для действительного числаобратным будет число.

Выражение запишем в стандартной форме. Для этого умножим числитель и знаменатель на комплексное число:

,

где .

Значит, для любого ненулевого комплексного числа существует обратное. Таким образом, операция деления определена как произведение делимого на число, обратное делителю.

Множество комплексных чисел является расширением множества действительных чисел, любое действительное число можно записать в виде.

Число называетсясопряженнымчислуи обозначается.

Сумма и произведение сопряженных чисел являются числами действительными:

;

.

Число называется модулем или абсолютной величиной комплексного числа. Очевидно, что.

Свойства сопряжения:

;

.

Каждому комплексному числу поставим в соответствие точкуплоскости, координатами которой в прямоугольной системе координат являются числаи.

Рис. 3.1.

Тогда каждой точке плоскости будет соответствовать единственное комплексное число. В результате получается взаимно однозначное соответствие между множеством комплексных чиселCи множеством точек плоскости, которое позволяет отождествить произвольное комплексное числос точкой плоскости, имеющей в выбранной системе координат координаты. При этом точки горизонтальной координатной осиизображают действительные числа и поэтому эту ось называютдействительной осью, а по вертикальной осиоткладываются мнимые части комплексных чисел, поэтому вертикальная осьназываетсямнимой осью.

Расстояние от точки до начала координат есть действительное неотрицательное число, которое называется модулем комплексного числаи обозначается. Угол между положительным направлением действительной оси и радиус-вектором точкиназывается аргументоми обозначается. Для числа 0 аргумент не определен, для остальных комплексных чисел аргумент определяется с точностью до целых кратных, при этом положительные углы отсчитываются против часовой стрелки.

Пусть . Из рис. 3.1 ясно, что модуль числанаходится по формуле. Аргумент числаопределяется из равенств,.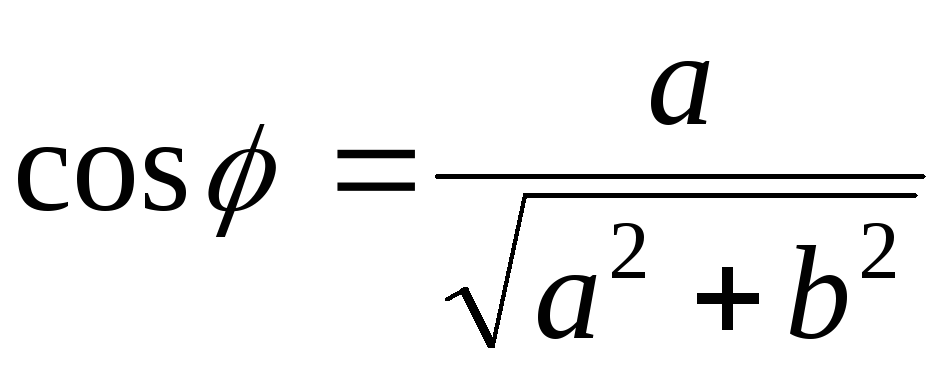

Отсюда:

(3.1)

Запись числа в виде (3.1) называется тригонометрической формой комплексного числа.

Если воспользоваться формулой Эйлера,

(3.2)

то от тригонометрической формы записи комплексного числа (3.2) несложно перейти к его показательной форме записи:

.

Пусть и‑ сопряженные числа. Если, то. Геометрическииявляются точками, симметричными относительно действительной оси (рис. 3.2). Отсюда вытекают равенства.

b





х

у



-

b

a

Рис. 3.2.

Перемножать и делить комплексные числа удобнее, если они представлены в тригонометрической форме:

(3.3)

В показательной форме:

При умножении комплексных чисел их аргументы складываются, а модули перемножаются. Это правило верно для любого числа сомножителей.

Аналогично,

(3.4)

При выполнении деления комплексных чисел в тригонометрической форме их аргументы вычитаются, а модули нужно разделить.