Контрольные вопросы к лекции №11

1. Понятие многочлена.

2. Условие равенства многочленов.

3. Сложение и умножение многочленов.

4. Теорема о делении с остатком.

5. Понятие корня многочлена.

6. Понятие кратности корня многочлена

7. Теорема Безу.

8. Схема Горнера.

9. Соотношение степени многочлена и числа его корней.

10. Понятие правильной рациональной дроби.

11. Разложение правильной рациональной дроби на простейшие.

12. Метод неопределенных коэффициентов.

Лекция 12. Квадратичные формы

Основные понятия:

квадратичная форма; матрица квадратичной формы; канонический вид квадратичной формы; нормальный вид квадратичной формы; канонический базис квадратичной формы; канонический базис Якоби; угловые миноры матрицы квадратичной формы; положительно определенная квадратичная форма; отрицательно определенная квадратичная форма; критерий Сильвестра.

Понятие квадратичной формы

Первоначально теория квадратичных форм использовалась для исследования кривых и поверхностей, задаваемых уравнением второго порядка, содержащими две или три переменные, Позднее эта теория нашла и другие приложения. В частности, при математическом моделировании экономических процессов целевые функции могут содержать квадратичные слагаемые. Многочисленные приложения квадратичных форм потребовали построения общей теории, когда число переменных равно любому , а коэффициенты квадратичной формы не всегда являются вещественными числами.

Квадратичной формойотнеизвестныхназывается сумма, каждое слагаемое которой является либо квадратом одного из неизвестных, либо произведением двух разных неизвестных.

Пример. Суммаявляется квадратичной формой от трех неизвестных.

Каждую квадратичную форму можно записать в стандартном виде. Для этого сначала приводятся подобные в квадратичной форме, затем коэффициенты при обозначаются через, а коэффициенты причерез, причемЧлензаписывается в виде. После этих преобразований квадратичную форму можно записать в виде:

Матрица:

называется матрицей квадратичной формы. Так как, то– симметричная матрица.

С учетом правила умножения матриц можно вывести матричную форму записи квадратичной формы.

,

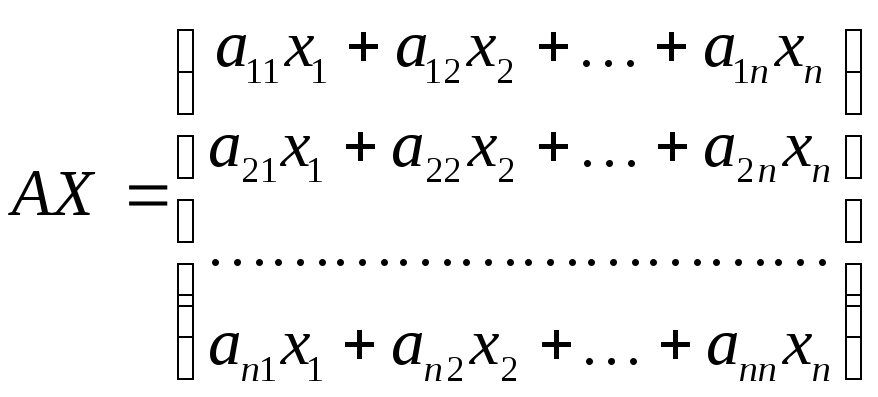где – матрица квадратичной формы,– матрица–столбец неизвестных:

Приведенные выкладки показывают, в частности, что если – симметрическая матрица, то выражениеявляется квадратичной формой от неизвестных, т.е. квадратичная форма является результатом скалярного произведения матрици. Матричная форма записи квадратичной формы имеет вид. Если– произвольный– мерный вектор, то после подстановки в квадратичную формувместополучится число, которое называетсязначением квадратичной формына векторе.

Канонический базис квадратичной формы

Принято считать, что квадратичная форма имеетканонический вид, если все коэффициенты при произведениях различных переменных равны нулю, т.е.при. При этом квадратичная форма представляет собой сумму квадратов переменных с соответствующими коэффициентами, т.е.:

.

В этом случае матрица квадратичной формы имеет диагональный вид:

Очевидно, что изучение свойств квадратичной формы, записанной в каноническом виде, значительно упрощается. В связи с этим возникает задача приведения произвольной квадратичной формы к каноническому виду. В основе многих известных методов приведения квадратичной формы к каноническому виду лежит следующая теорема.

Теорема. Всякая квадратичная форма с помощью невырожденного линейного преобразования может быть приведена к каноническому виду.

Метод ортогональной матрицы использует особенности собственных значений и собственных векторов симметрической матрицы.

Пусть дана квадратичная форма , Поскольку– симметрическая матрица, для нее существует диагонализирующая ортогональная матрица, такая что:

где – собственные значения матрицы.

Применим к квадратичной форме линейное преобразование , где– матрица-столбец новых переменных;– матрица, обратная к.

Таким образом, квадратичную форму всегда можно представить в каноническом виде с коэффициентами, равными собственным значениям матрицы квадратичной формы.

Канонический вид квадратичной формы определяется неоднозначно. В то же время можно доказать, что все канонические формы, к которым приводится данная квадратичная форма, содержат одинаковое число отрицательных, положительных и нулевых коэффициентов при квадратах новых переменных.

Наиболее удобным для исследования является канонический вид, в котором коэффициенты при новых переменных равны +1 или –1, т.е. квадратичная форма имеет вид:

.

Такую запись называют нормальным видом квадратичной формы. В нем общее число квадратов равно рангуквадратичной формы.

Квадратичная форма может быть приведена к нормальному виду многими различными преобразованиями. При этом справедлива следующая теорема.

Теорема. Число положительных и число отрицательных квадратов в нормальном виде, к которому приводится данная вещественная квадратичная форма вещественным невырожденным линейным преобразованием, не зависит от выбора этого преобразования.

Эту теорему называют законом инерции квадратичных форм.

Базис пространстваназываетсяканоническим базисом квадратичной формы , если в этом базисе квадратичная форма имеет канонический вид, т.е.при.

Если – канонический базис, то выражение:

,

называется каноническим видом в базисе, где– новый набор неизвестных.

Теорема. Если – разложение векторапо каноническому базисуквадратичной формы, то значениена векторевычисляется по формуле,.

Доказательство:

Эта теорема утверждает, что если известны канонический базис квадратичной формыи ее канонический видв этом базисе, то для вычисления значенияквадратичной формына векторе достаточно:

1. разложить вектор по каноническому базису :

;

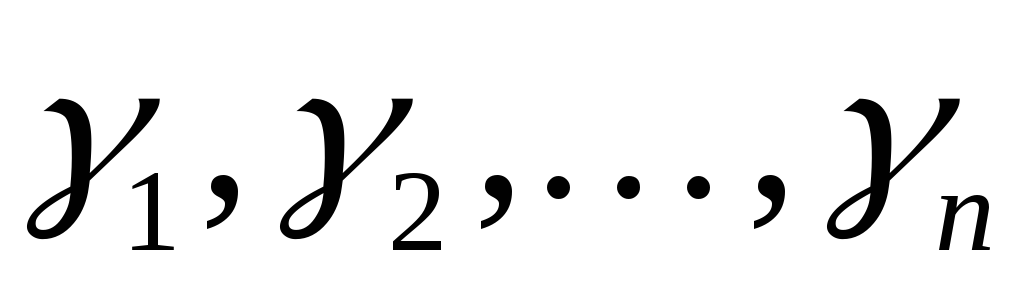2. коэффициенты разложения подставить вместо неизвестныхв канонический вид квадратичной формы:

.

Квадратичная форма имеет много разных канонических базисов. Процесс построения канонического базиса называется приведением квадратичной формы к сумме квадратов.

Наиболее часто используются: канонический базис из собственных векторов матрицы и канонический базис Якоби.