Канонический базис из собственных векторов матрицы квадратичной формы

Теорема.Ортонормированный базис пространства , состоящий из собственных векторовсимметрической матрицы,, является каноническим базисом квадратичной формы, а выражение– ее каноническим видом в базисе.

Доказательство:

, если, так как – ортогональная система векторов – канонический базис квадратичной формы.

, так как векторы системы нормированы, то,.

Канонический базис Якоби квадратичной формы

Будем говорить, что матрица удовлетворяет условию Якоби, если определители:

,,

называемые угловыми минорамиматрицы_,не равны нулю. Очевидно, что,.

Обозначим через матрицу:

.

Вычислим определитель этой матрицы, разлагая ее по последнему столбцу, затем также по последнему столбцу разложим полученный определитель и т.д.

Из условия ,следует, чтои, значит, каждая система уравнений,, где––й вектор диагональной системы, имеет единственное решение,. Система векторовназывается системой векторов Якоби матрицы, которая удовлетворяет условию Якоби.

Теорема.Если матрица квадратичной формыудовлетворяет условию Якоби, то система векторов Якобиматрицыявляется каноническим базисом квадратичной формы, а выражение:

–ее каноническим видом в базисе .

Положительно и отрицательно определенные квадратичные формы

Квадратичная форма называетсяположительно определенной, если значениена каждом ненулевом значениибольше нуля, т.е.:

, если,

Если же на каждом, то квадратичная форма называетсяотрицательно определенной.

Теорема.Дана квадратичная форма , – ее канонический базис, а выражение ,канонический видв базисе. Тогда справедливы следующие утверждения:

1. Квадратичная форма положительно определена тогда и только тогда, когда,,…,.

2. Квадратичная форма отрицательно определена тогда и только тогда, когда,,…,.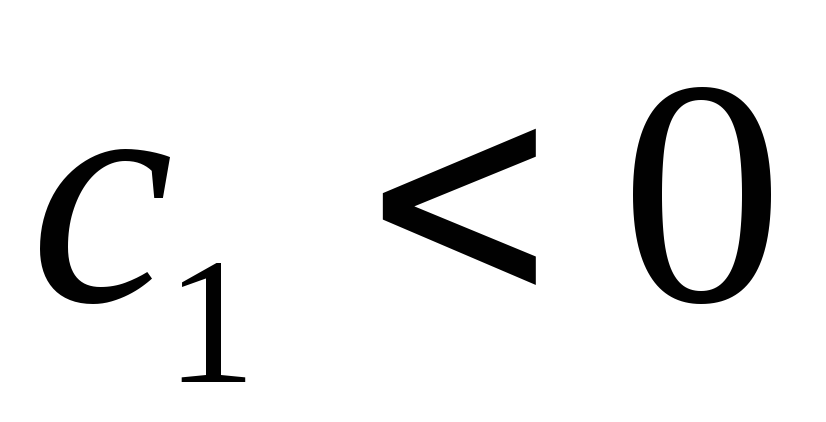

Доказательство:

Необходимость. Дано, что– положительно определенная форма. Так как, тои поэтому.

Достаточность. Дано, что в каноническом виде все коэффициенты ,,…,_.Нужно доказать, чтоположительно определена. Рассмотрим произвольный ненулевой вектори разложим его по базису:

Так как , то в разложениине все коэффициенты равны нулю. Следовательно, так как ,,…,и среди чиселхотя бы одно отлично от нуля.

Аналогично доказывается и второе утверждение.

Эта теорема дает два наиболее употребляемых критерия положительной и отрицательной определенности квадратичной формы.

Теорема.Дана квадратичная форма . Тогда справедливы следующие утверждения:

1. Квадратичная форма положительно определена тогда и только тогда, когда все собственные значения матрицыположительны.

2. Квадратичная форма отрицательно определена тогда и только тогда, когда все собственные значения матрицыотрицательны.

Доказательство:

Докажем первое утверждение. Рассмотрим ортонормированный базис пространства, состоящий из собственных векторов симметрической матрицы, и пусть,. Тогда– канонический базис квадратичной формы , а выражение – ее канонический вид в базисе. Теперь первое утверждение этой теоремы вытекает из первого предложения предыдущей теоремы.

Второе предложение доказывается аналогично.

Лемма. Если какой-нибудь угловой минор матрицыравен нулю, то найдется такой ненулевой вектор, что_.

Теорема (Критерий Сильвестра). Справедливы следующие утверждения:

1. Квадратичная форма положительно определена тогда и только тогда, когда главные миноры матрицыположительны.

2. Квадратичная форма отрицательно определена тогда и только тогда, когда главные миноры матрицычетного порядка положительны, а главные миноры матрицынечетного порядка отрицательны.

Доказательство: Докажем первое утверждение.

Необходимость. Дано, чтоположительно определена. Покажем, что все угловые миноры матрицыотличны от нуля. Допустим обратное, и пусть. Тогда согласно Лемме найдется такой ненулевой вектор, что . Однако это противоречит положительной определенности квадратичной формы.

Итак, матрица удовлетворяет условию Якоби, поэтому можно построить систему векторов Якоби, которая является каноническим базисом, причем выражение –ее канонический вид в базисе. Теперь из положительной определенности квадратичной формы и первого утверждения доказанной ранее теоремы следует, что , и значит, что.

Достаточность. Если, то угловые миноры матрицыотличны от нуля, и можно построить канонический базис квадратичной формы, в котором 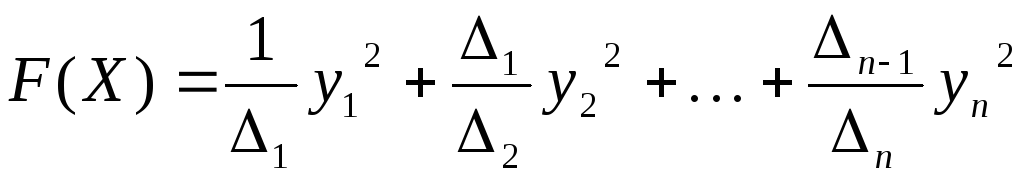–канонический вид квадратичной формы. Поскольку , тоположительно определена.

Аналогично доказывается второе утверждение теоремы.