Взаимное расположение прямых

Пусть даны две прямые:

и.

Эти прямые заданы своими точками ии направляющими векторамии. Поэтому:

.

Параллельность или перпендикулярность прямых равносильна, соответственно, параллельности или перпендикулярности их направляющих векторов. Поэтому условие перпендикулярности прямыхможно записать в виде:

или.

Условие параллельности:.

Возможны четыре случая взаимного расположения прямых:

1. Прямые совпадают:, т.е.

.

2. Прямые параллельны:непараллелен, но, т.е..

3. Прямые пересекаются:непараллелен, но,,‑ компланарны, т.е.

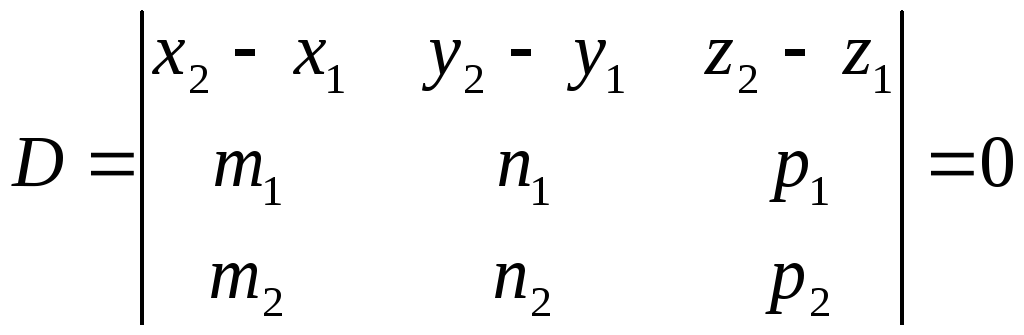
   (5.8)

4. Прямые скрещиваются:,,‑ некомпланарны, т.е..

Условие (5.8) выполняется в случаях I-IIIи означает, что прямые лежат в одной плоскости.

Контрольные вопросы к лекции №5

1. Общее уравнение прямой.

2. Понятие направляющего и нормального вектора прямой.

3. Каноническое уравнение прямой.

4. Векторное параметрическое уравнение прямой.

5. Уравнение прямой, проходящей через две точки.

6. Расчет угла между прямыми.

7. Условия пересечения, параллельности и перпендикулярности прямых.

Лекция 6. Плоскость

Основные понятия:

поверхность; поверхность -го порядка; общее уравнение плоскости; нормальный вектор плоскости; уравнение плоскости в отрезках; нормальное уравнение плоскости; отклонением точки от плоскости.

Основные понятия

Всякая поверхностьв пространстве задается в декартовых координатах уравнением вида.

Если ‑ многочлен-й степени, то соответствующая поверхность называется алгебраической поверхностью-го порядка или простоповерхностью -го порядка.

Всякая поверхность 1-го порядка есть плоскость, т.е. всякое уравнение 1-й степени:

(6.1)

определяет плоскость. Уравнение (6.1) называется общим уравнением плоскости.

Вектор , координатами которого являются коэффициенты прив уравнении (6.1), перпендикулярен плоскости (6.1) по свойству скалярного произведения векторов. Этот факт будет постоянно использоваться в дальнейшем. Векторназываютнормальным вектором плоскости(6.1).

Уравнение плоскости, проходящей через данную точку перпендикулярно вектору, имеет вид:

(6.2)

Очевидно, что уравнение (6.1) имеет смысл только тогда, когда хотя бы один из коэффициентов не равен нулю.

Рассмотрим частные случаи.

I. D ≠ 0.

1. Если , то уравнениеопределяет плоскость, параллельную оси, так как вектор нормали к этой плоскости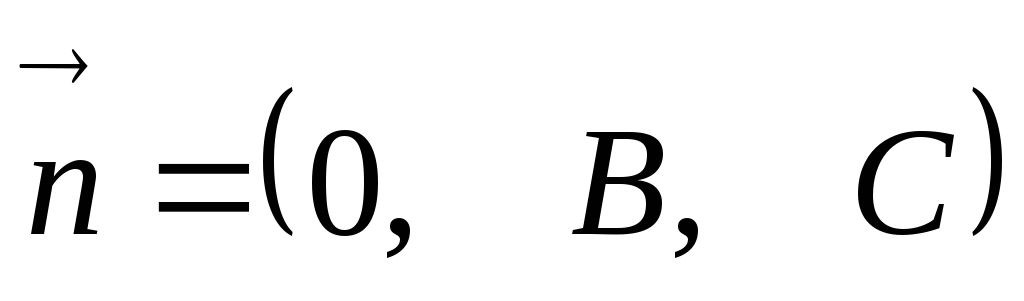перпендикулярен оси(проекция ненулевого вектора на ось равна нулю тогда, когда он перпендикулярен этой оси).

2. Аналогично, если , то уравнениеопределяет плоскость, параллельную оси.

3. Если . То уравнениеопределяет плоскость, параллельную оси.

4. Если , то уравнение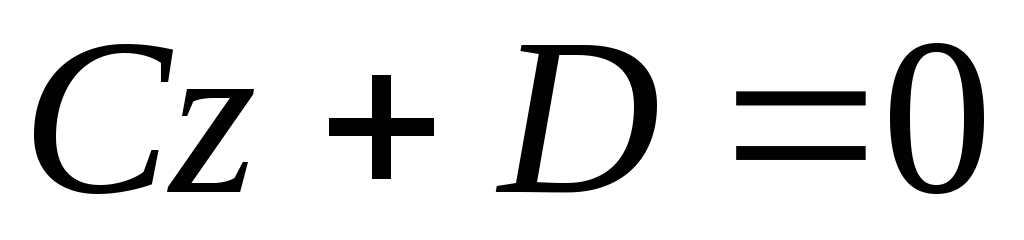илиопределяет плоскость, параллельную плоскости. В этом случае вектор нормалиперпендикулярен к осями, т.е. к плоскости.

5. При имеемили‑ уравнение плоскости, параллельной координатной плоскости.

6. Если , то уравнениеилиопределяет плоскость, параллельную плоскости.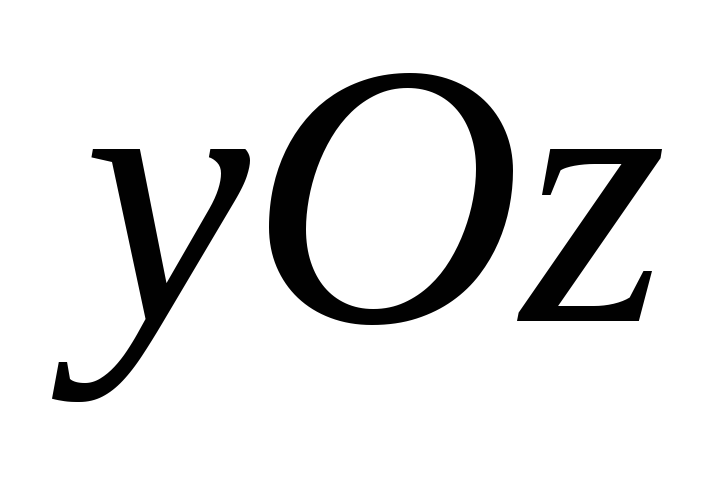

_{II. D = 0.}

1. Если , то уравнениеопределяет плоскость, проходящую через начало координат, так как координаты точкиудовлетворяют этому уравнению.

2. Если , то уравнениеопределяет плоскость, вектор нормали которой. Эта плоскость проходит через ось.

3. Аналогично, если , то уравнениеопределяет плоскость, проходящую через ось.

4. Если , то уравнениеопределяет плоскость, проходящую через ось.

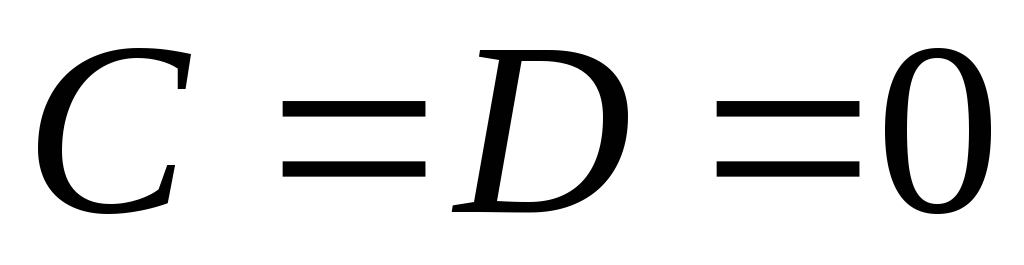5. Если , то уравнениеилиопределяет плоскость. Аналогично, уравненияиопределяют соответственно плоскостии.

Если в уравнении (6.1) все коэффициенты отличны от нуля, то это уравнение может быть преобразовано куравнению плоскости в отрезках:

(6.3)

Здесь ‑ величины отрезков, отсекаемых плоскостью на осях координат.