Нормальное уравнение плоскости

Нормальным уравнением плоскостиназывается уравнение:

,

(6.4)

где ‑ углы между перпендикуляром, опущенным из начала координат на плоскость, и положительным направлением осей координат, а‑ расстояние от плоскости до начала координат.

Нормальное уравнение отличается от общего уравнения тем, что в нем коэффициенты при являются координатами единичного вектора, перпендикулярного плоскости, а свободный член – отрицательный.

Общее уравнение (1) приводится к нормальному виду умножением его на нормирующий множитель , при этом знак выбирается противоположным знаку свободного члена(если, знак можно выбрать любой).

Отклонением точкиот плоскости называется ее расстояниеот плоскости, взятое со знаком плюс, если точкаи начало координатлежат по разные стороны от плоскости (Рис. 6.1), и со знаком минус – еслиилежат по одну сторону от плоскости.

Отклонение точки от плоскости определяется по формуле.

Следовательно, чтобы найти расстояние от точки до плоскости, надо привести уравнение плоскости к нормальному виду и в его левую часть вместо подставить координаты точки. Получим отклонение. А расстояние.

Взаимное расположение плоскостей

Пусть даны плоскости и. Угол между ними равен углу между перпендикулярными к ним векторами. Косинус этого угла вычисляется по формуле:

(6.5)

Плоскости параллельны, если иколлинеарны, т.е.:

(6.6)

Условие перпендикулярности плоскостей ‑ , т.е.:

(6.7)

Если даны три плоскости:

,

(6.8)

то их общие точки определяются системой уравнений (6.8).

В случае, если перпендикулярные этим плоскостям векторы ,,некомпланарны, три плоскости имеют единственную общую точку.

В самом деле, тогда смешанное произведение 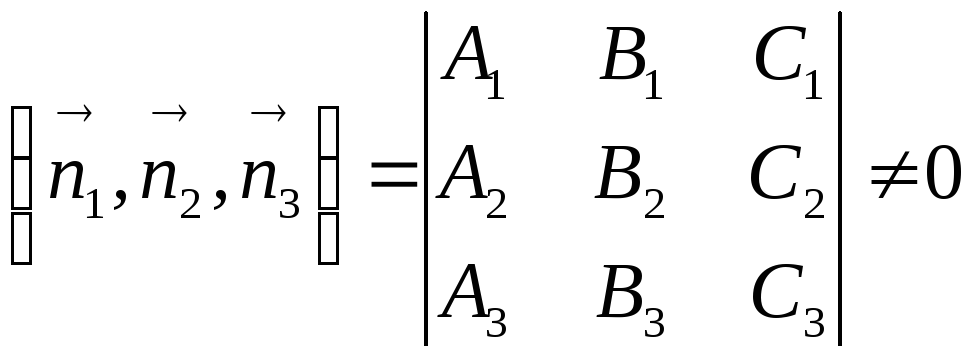, а записанный определитель является определителем системы уравнений (6.8), и, следовательно, система (6.8) имеет единственное решение.

Контрольные вопросы к лекции №6

1. Понятие поверхности -го порядка.

2. Общее уравнение плоскости.

3. Понятие нормального вектора плоскости.

4. Уравнение плоскости в отрезках.

5. Нормальное уравнение плоскости.

6. Вычисление отклонения точки от плоскости.

Лекция 7. Кривые второго порядка

Основные понятия:

эллипс; гипербола; парабола; фокусы эллипса; уравнение эллипса; каноническое уравнение эллипса; эксцентриситет эллипса; фокальные радиусы; директрисы эллипса; фокусы гиперболы; каноническое уравнение гиперболы; асимптота гиперболы; оси гиперболы; вершины гиперболы; полуоси гиперболы; эксцентриситет гиперболы; фокальные радиусы гиперболы; директрисы гиперболы; каноническое уравнение параболы; ось параболы.

Уравнение фигуры

Геометрической фигуройили просто фигурой на плоскости называется множество точек. Задать фигуру – значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестнымиизаписывается в виде. Если выбрать на плоскости некоторую прямоугольную систему координат, то в ней уравнение называется уравнением фигурыпри выполнении следующих двух условий:

1. Если точка принадлежит фигуре, то координатыявляются решениями уравнения, т.е.;

2. если пара чисел является решением уравнения, то точкапринадлежит фигуре_.

Это определение в более компактной записи выглядит следующим образом. Уравнение называется уравнением фигуры, если, то есть– решение уравнения.

Из определения уравнения фигуры следует, что фигура состоит только из тех точек плоскости, координаты которых являются решениями уравнения, т.е. уравнение фигуры задает эту фигуру.

Возможны два вида задач:

1. дано уравнение и надо построить фигуру, уравнением которой является;

2. дана фигура и надо найти уравнение этой фигуры.

Первая задача сводится к построению графика уравнения и решается, чаще всего, методами математического анализа.

Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:

1. Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);

2. Записать в координатах условие, сформулированное в первом пункте.

Эллипс

Эллипсомназывается линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точекиесть величина постоянная (большая, чем расстояние междуи).

Точки иназываются фокусами эллипса. Обозначив расстояние между фокусами через, а сумму расстояний от точек эллипса до фокусов через, имеем. Если это условие не выполнено, то рассматриваемое множество точек либо отрезок прямой, заключенной между фокусами, либо не содержит ни одной точки.

Из определения эллипса вытекает следующий метод его построения: если концы нерастяжимой нити длины закрепить в точкахии натянуть нить острием карандаша, то при движении острия будет вычерчиваться эллипс с фокусамиии с суммой расстояний от произвольной точки эллипса до фокусов, равной(Рис. 7.1).

Рис. 7.1.

Составим уравнение эллипса. Для этой цели расположим декартову прямоугольную систему координат таким образом, чтобы ось походила через фокусыи, положительное направление оси – отк, начало координат выберем в середине отрезка. Тогда координаты точекибудут соответственнои.

Пусть ‑ произвольная точка эллипса, тогда:

,

.

По определению эллипса . Подставляя сюда значенияи, имеем:

(7.1)

Уравнение (1) и есть уравнение эллипса. Преобразуя, упростим его:

Возведя обе части уравнения в квадрат и приведя подобные члены, получим: .

Возведем еще раз обе части в квадрат и приведем подобные члены. Получаем или

(7.2)

Положительную величину обозначим через. Тогда уравнение (7.2) примет вид:

(7.3)

Оно называется каноническим уравнение эллипса.

Координаты точек эллипса ограничены неравенствами . Значит, эллипс ограниченная фигура, не выходящая за пределы прямоугольника со сторонамии_:

O

-

-c

c

b

-b

a

-a

2a

2b

Рис.

7.3

x

y

Рис. 7.3.

Заметим, что в уравнение (7.3) входят лишь четные степени и. Поэтому, если точкапринадлежит эллипсу, то и точки,,также ему принадлежат. А это означает, что эллипс – линия симметричная относительно координатных осейи.

Поэтому для исследования формы эллипса достаточно рассмотреть его в первой координатной четверти, а в остальных четвертях его строение определяется по симметрии. Для первой четверти, из уравнения (7.3) имеем:

(7.4)

При возрастании отдо,монотонно убывает отдо. График функции изображен на Рис. 7.4.

Рис. 7.4

Достроив остальные четверти эллипса по симметрии, получим весь эллипс (Рис. 7.5).

Оси симметрии эллипса (оси и) называются просто его осями, а центр симметрии – точка‑ центром эллипса. Точкипересечения эллипса с осями координат называются вершинами эллипса. Отрезкии, а также их длиныиназываются полуосями эллипса. В случае, когда фокусы эллипса находятся на оси(как в нашем случае), из равенства, следует, что. В этом случаеназывается большой полуосью, а‑ малой.

Если , то уравнение (7.3) можно переписать в виде:

(7.5)

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси . Пусть на плоскости выбрана прямоугольная система координат. Тогда преобразование, переводящее произвольную точкув точку, координаты которой задаются формулами, будет окружность (4) переводить в эллипс, заданный соотношением.

Ч

y

ислоназываетсяэксцентриситетом эллипса. Эксцентриситетхарактеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличениистановится более вытянутым (Рис. 7.6).

0





 =0,6

a

-

a

-b

b

Рис. 7.6.

 =0,8

х

Фокальными радиусами точки эллипса называются отрезки прямых, соединяющие эту точку с фокусамии. Их длиныизадаются формуламии. Прямыеназываютсядиректрисами эллипса. Директрисаназывается левой, а‑ правой. Так как для эллипса, тои, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины.

Директрисы обладают следующим свойством: отношение расстояния любой точки эллипса от фокуса к ее расстояниюдо соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е..