Задача линейного программирования

В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися. В случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической. Каноническая задача линейного программирования в координатной форме записи имеет вид:

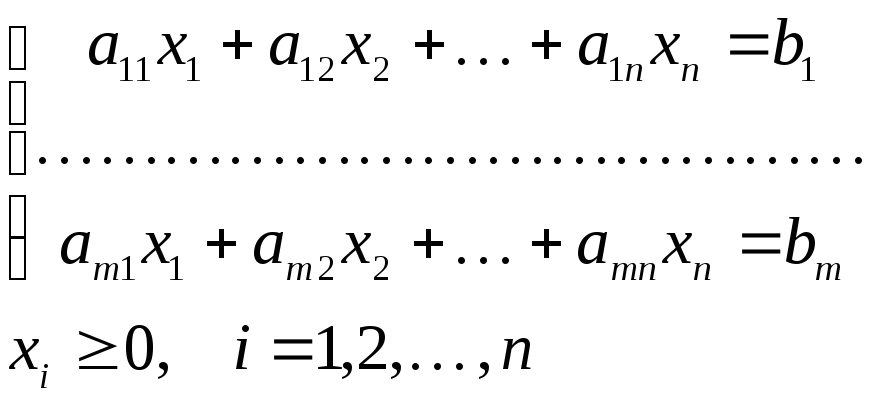
Используя знак суммирования эту задачу можно записать следующим образом:

Каноническая задача линейного программирования в векторной форме имеет вид:

В данном случае введены векторы:

,

,,

Здесь – скалярное произведение векторови.

Каноническая задача линейного программирования в матричной форме записи имеет вид:

где:

,.

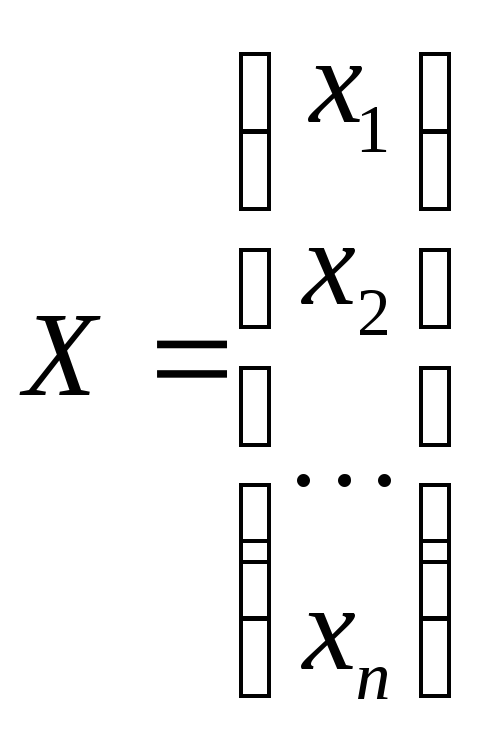Здесь – матрица коэффициентов системы уравнений,– матрица-столбец переменных задачи;– матрица-столбец правых частей системы ограничений.

Нередко используются задачи линейного программирования, называемые симметричными, которые в матричной форме записи имеют вид:

или

Приведение общей задачи линейного программирования к канонической форме

В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Однако, при составлении математических моделей экономических задач ограничения в основном формулируются системы неравенств, поэтому возникает необходимость перехода от системы неравенств к системе уравнений. Это может быть сделано следующим образом. К левой части линейного неравенства:

прибавляется величина , такая, что переводит неравенство в равенство, где:

.

Неотрицательная переменная называетсядополнительнойпеременной.

Основания для возможности такого преобразования дает следующая теорема.

Теорема.Каждому решению неравенства

соответствует единственное решение уравнения:

и неравенства , и, наоборот, каждому решениюуравнения:

и неравенства соответствует единственное решениенеравенства:

.

Доказательство.Пусть– решение неравенства. Тогда:

или

Если в уравнение вместо переменных подставить значения=, получится:

Таким образом, решение удовлетворяет уравнению:

и неравенству.

Доказана первая часть теоремы.

Пусть удовлетворяет уравнениюи неравенству, т.е.и. Отбрасывая в левой части равенства неотрицательную величину, получим:

_,

т.е. удовлетворяет неравенству:

_,

что и требовалось доказать.

Если в левую часть неравенств системы ограничений вида ,добавить переменную,, то получится система ограничений – уравнений,. В случае, если система неравенств–ограничений имеет вид,, то из левой части неравенств–ограничений нужно вычесть соответствующую неотрицательную дополнительную переменную,.

Полученная таким образом система уравнений–ограничений, вместе с условиями неотрицательности переменных, т.е. ,и целевой функцией является канонической формой записи задачи линейного программирования.

Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому не влияют на ее значения.

В реальных практических задачах дополнительные неизвестные имеют определенный смысл. Например, если левая часть ограничений задачи отражает расход ресурсов на производство продукции в объемах ,, а правые части - наличие производственных ресурсов, то числовые значения дополнительных неизвестных,означают объем неиспользованных ресурсов-го вида.

Иногда возникает также необходимость перейти в задаче от нахождения минимума к нахождению максимума или наоборот. Для этого достаточно изменить знаки всех коэффициентов целевой функции на противоположные, а в остальном задачу оставить без изменения. Оптимальные решения полученных таким образом задач на максимум и минимум совпадают, а значения целевых функций при оптимальных решениях отличаются только знаком.