Отношения эквивалентности и упорядоченности

В математике понятие отношения используется для обозначения какой-либо связи между объектами. Отношениеесть некоторое множество упорядоченных пар, где, а.

• Отношение называется рефлексивным, если каждый элемент множества находится в этом отношении сам с собой ().

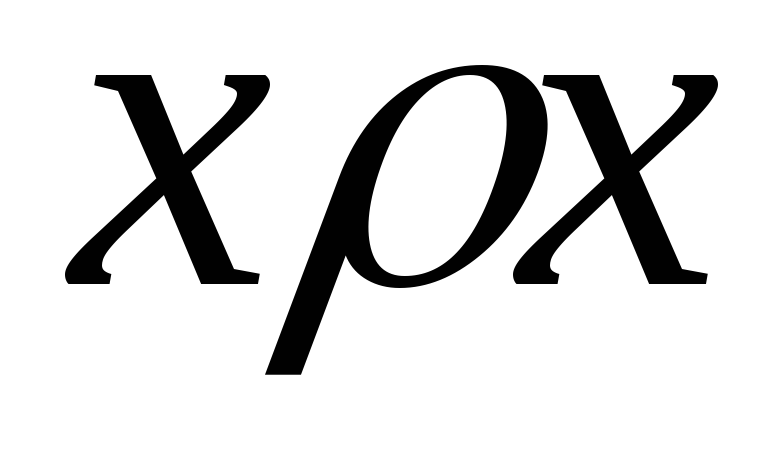• Отношение называется симметричным, если оно обладает свойством коммутативности ().

• Отношение называется транзитивным, если_.

• Отношение называется антисимметричным,если_.

Часто приходится рассматривать несколько элементов множества как эквивалентные, потому что по определенным признакам один элемент может быть заменен другим. Так, например, по признаку величины дроби иэквивалентны. Отношение эквивалентности рефлексивно, симметрично и транзитивно. Понятие эквивалентности подразумевает выполнение следующих условий:

• каждый элемент эквивалентен самому себе;

• высказывание, что два элемента являются эквивалентными, не требует уточнения, какой из элементов рассматривается первым;

• два элемента, эквивалентные первому, эквивалентны между собой.

Пусть – множество, в котором определено отношение эквивалентности. Подмножество элементов, эквивалентных элементу, называется классом эквивалентности: все элементы этого класса эквивалентны между собой и всякий элементиз находится в одном и только в одном классе (если элементов, эквивалентных, не существует, томожет быть и единственным элементом класса). Отношение эквивалентности в определяет на разбиение на классы эквивалентности, т.е. становится объединением непересекающихся классов.

Особенности природы элементов множества в большинстве случаев позволяют установить между ними отношения полного (или совершенного) порядка. Это отношение по определению обладает следующими свойствами:

Если между элементами множества определено также и отношение эквивалентности, то между элементами устанавливается отношение неполного или нестрогого порядка:

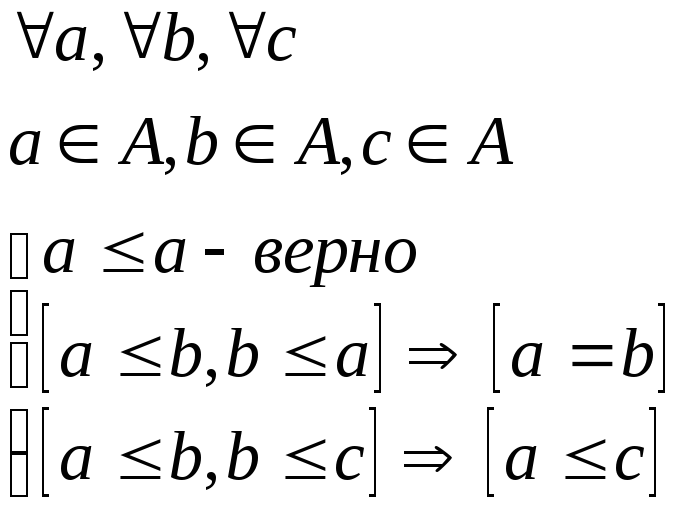
Возможны случаи, когда некоторые элементы множества не сравнимы. Такие множества называются частично упорядоченными.

Контрольные вопросы к лекции №2

1. Понятие множества.

2. Основные операции над множествами.

3. Понятие отображения.

4. Понятие области определения отображения.

5. Охарактеризовать по отдельности инъективное, сюръективное и биективное отображения.

6. Понятие мощности множества.

7. Сравнение бесконечных множеств.

8. Счетные и несчетные множества.

9. Понятие эквивалентности.

10. Охарактеризовать упорядоченные и частично упорядоченные множества.

Лекция 3. Числовые множества

Основные понятия:

счетные множества; несчетные множества; числовые множества; ограниченным сверху (снизу) множества; верхняя (нижняя) грань множества; граничная точка множества; граница множества; комбинаторика; соединения; размещения; перестановки; сочетания; множество комплексных чисел; комплексное число; действительная часть комплексного числа; мнимая часть комплексного числа; число ; сложение комплексных чисел; умножение комплексных чисел; тригонометрическая форма комплексных чисел; абсолютная величина комплексного числа; аргумент комплексного числа; комплексно сопряженное число; формула Муавра.

Основные понятия

Будем рассматривать множества, элементами которых являются числа. Такие множества называются числовыми. Числовые множества задаются на оси действительных чиселR. На этой оси выбирают масштаб и указывают начало отсчета и направление. Наиболее распространенные числовые множества:

• ‑ множество натуральных чисел;

• ‑ множество целых чисел;

• – множество рациональных или дробных чисел;

• ‑ множество действительных чисел.

Множество всех рациональных чисел является счетным множеством. Счетным является множествовсех точек плоскости (пространства) имеющих рациональные координаты.

Множество всех действительных чисел является несчетным: оно имеет мощность, называемуюконтинуумом.

Некоторое непустое подмножество множества действительных чисел называютограниченным сверху (снизу), если существует действительное число такое, что выполняется неравенство().

Всякое число с указанным свойством называютверхней (нижней) граньюмножества.

Непустое подмножество множества действительных чисел называетсяограниченным, если оно ограничено и сверху и снизу.

В противоположность этому определению, множество называется неограниченным сверху (снизу), если какое бы число мы бы не предложили в качестве верхней (нижней) границы множества, всегда найдется элемент этого множества, который будет больше (меньше) .

Множество, неограниченное как сверху, так и снизу, называется неограниченным множеством.

Наименьшую из верхних граней непустого подмножества множества действительных чисел называютточной верхней граньюэтого множества и обозначаютsup . Наибольшую из нижних граней непустого подмножества множества действительных чиселназываютточной нижней граньюэтого множества и обозначаютinf . Символыsupиinfявляются сокращениями отsupremum (самый верхний) и infimum(самый нижний).

Примем без доказательства утверждение о том, что всякое ограниченное сверху (снизу) множество имеет точную верхнюю (нижнюю) грань.

Граничной точкоймножества называется точка, у которой в любом содержащем ее открытом промежутке найдутся как точки, принадлежащие множеству, так и точки, не принадлежащие множеству. Сама граничная точка может, как принадлежать множеству, так и не принадлежать ему.

Граница множества– совокупность граничных точек множества:

• (множество натуральных чисел) ограниченно снизу (например, числом) и не ограничено сверху;

• (множество действительных чисел) неограничено;

• множество отрицательных чисел неограничено снизу и ограничено сверху.