§2. Системы координат

Задать систему координат (на прямой, на плоскости, в пространстве) – это значит указать способ, позволяющий устанавливать положение точек (прямой, плоскости, пространства) с помощью чисел.

Когда речь заходит о системе координат необходимо различать два момента: 1) чем задается, определяется система координат; 2) что такое координаты точки.

I Система координат на прямой

Чтобы задать СК на прямой достаточно превратить ее в числовую ось, т.е. выбрать направление и две точки. Координатой точки А служит то действительное число x, которое изображает точка А: х=±d(A,0). Тот факт, что точка А имеет координату х записывают в виде А(х). Расстояние между точками A₁(х₁) и A₂(х₂) вычисляется по формуле

d(A₁,A₂)=|х₂-х₁|.

II Декартова прямоугольная система координат на плоскости

Задается двумя взаимно перпендикулярными числовыми осями с общим началом отсчета, равными единичными отрезками, причем указано, какая из них считается первой, а какая второй.

Общее начало отсчета называется началом координат и обозначается буквой О. Оси называются координатными осями или осями координат. Первую из них называют осью абсцисс и обозначают символом Ох, а вторую – осью ординат, обозначают Оу.

П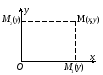устьМ – произвольная точка плоскости. Спроектируем ее на координатные оси, т.е. опустим перпендикуляры из М на Ох и Оу. Основания этих перпендикуляров обозначим М₁ и М₂ соответственно. Эти точки, каждая на своей оси, имеют определенные координаты: М₁(х) и М₂(у).

Число х называется абсциссой точки М, а у – ординатой точки М.

Тот факт, что точка плоскости М имеет координаты х и у записывают

в виде М(х,у).

Расстояние между точками А₁(х₁,у₁) и А₂(х₂,у₂) вычисляется по формуле

.

К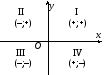аждая ось разбивает плоскость на две полуплоскости: верхнюю и нижнюю (осьОх), правую и левую (ось Оу). Две оси вместе разбивают плоскость на 4 квадранта (четверти). Нумерация квадрантов и знаки координат показаны на рисунке

III дпск в пространстве

Задается тремя взаимно перпендикулярными числовыми осями с общим началом отсчета и одинаковыми единичными отрезками. Оси занумерованы в некотором порядке, т.е. указано, какая из них считается первой, какая второй и какая третьей.

Первая и вторая называются так же, как и в предыдущем пункте, а третья называется осью аппликат и обозначается Оz.

Каждая пара осей определяет плоскость, которая называется координатной. Обозначения:хОу, хОz и уОz. Каждая плоскость разбивает пространство на два полупространства. В частности, горизонтальная плоскость хОу разбивает на верхнее (расположено в положительном направлении оси Oz)

и нижнее полупространства

Пусть М – произвольная точка пространства. Спроектируем ее на плоскость хОу. Получим точку М₁, которая на этой плоскости имеет вполне определенные координаты х и у. Они называются абсциссой и ординатой точки М. Третья координата – аппликата – точки М определяется формулой

z = ±d(M,M₁),

причем знак ''+'' выбираем, если М лежит в верхнем полупространстве, а знак ''–'', если в нижнем.

Расстояние между точками М(х₁,у₁,z₁) и N(х₂,у₂,z₂) вычисляется по формуле

.

Если точка С(х,у,z) делит данный отрезок MN в отношении λ

( т.е. МС: СN=λ ), то

.

Если требуется найти координаты середины отрезка MN, достаточно положить в этих формулах λ=1.