II Канонические уравнения прямой

Определение. Всякий ненулевой вектор, лежащий на данной прямой или параллельный ей, называется ее направляющим вектором. Обозначение: .

Составим уравнение прямой, проходящей через точку M₀(x₀,y₀,z₀) в направлении вектора . Возьмем текущую точку прямойM(x,y,z) и рассмотрим вектор . Он лежит на данной прямой и поэтому коллинеарен ее направляющему вектору. Осталось написать условие коллинеарности, т.е. пропорциональность проекций:

. (2)

Это и есть канонические уравнения прямой, проходящей через точку M₀(x₀,y₀,z₀) и имеющей направляющий вектор .

Пример. Найти канонические уравнения прямой

(3)

Решение. Чтобы составить канонические уравнения прямой, нужно: 1) найти какую-либо точку прямой; 2) найти направляющий вектор прямой.

1) Найти какую-нибудь точку прямой (3) – это означает найти какое-нибудь решение этой системы двух уравнений с тремя неизвестными. Положим, например, x=0. Система (3) превратится в

Отсюда нетрудно найти: z=2, y= –6. Итак, точка M₀(0;–6; 2) принадлежит прямой (3).

2) Прямая определена как пересечения двух плоскостей, значит она лежит в каждой из них и поэтому перпендикулярна их нормальным векторам и. В качестве направляющего вектора можно взять любой вектор перпендикулярный к векторами, например, их векторное произведение

,

или вектор, коллинеарный ему . Итак, искомые канонические уравнения имеют вид

Пример. Составить уравнения прямой, проходящей через точки M₁(x₁,y₁,z₁) и M₂(x₂,y₂,z₂).

Решение. Для того, чтобы использовать канонические уравнения (2), положим M₀=M₁, . Получим:

. (4)

Имея эти уравнения, предыдущей пример можно решить, не находя направляющий вектор прямой. Надо только найти не одну точку, лежащую на прямой, а две.

III Параметрические уравнения прямой

Пусть даны канонические уравнения какой-либо прямой. Обозначим буквой t каждое из трех равных отношений, которые участвуют в канонических уравнениях:

.

Отсюда:

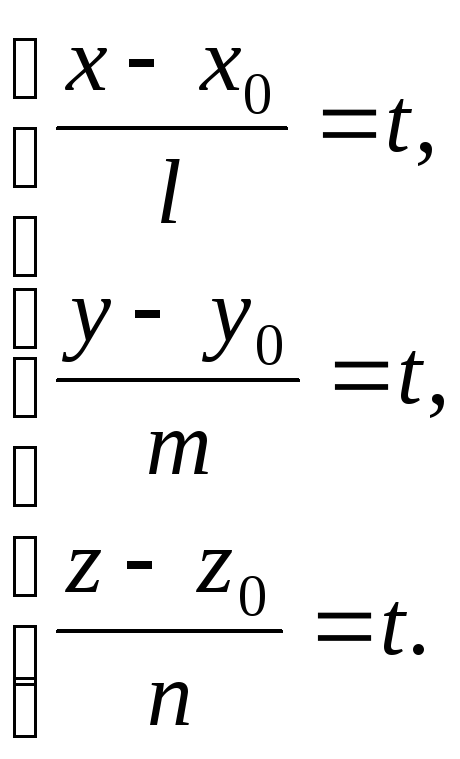
И окончательно

(5)

Это и есть параметрические уравнения прямой, проходящей через точку M₀(x₀,y₀,z₀) в направлении вектора . Эти уравнения удобно применять в тех случаях, когда требуется найти точку пересечения прямой и плоскости.

Пример. Найти проекцию данной точки M₀(5, 2,–1) на плоскость α: 2x–y+3z+23=0.

Решение. Проведем через M₀ прямую ; ее направляющим вектором служит нормальный вектор плоскостиИмеем параметрические уравнения (5)

Проекция точки M₀ на плоскость α – это точка пересечения прямой p с плоскостью α, ее координаты – это решение системы, составленной из уравнения плоскости и уравнений прямой. Подставим параметрические уравнения прямой в общее уравнение плоскости:

2(5+2t)–(2–t)+3(–1+3t)+23=0.

Отсюда t= –2 и координаты искомой точки имеют вид:

x=5+2(–2)=1; y=2–(–2)=4; z= –1+3(–2)= –7.

§8. Расстояние от точки до прямой в пространстве

Получим формулу для вычисления расстояния d(M^*, p) от точки M^*(x^*,y^*,z^*) до прямой

.

Будем считать, что направляющий вектор прямой лежит на прямой и приложен в ее точкеM₀(x₀,y₀,z₀). Рассмотрим параллелограмм, построенный на векторах и. Его высотаh, опущенная из вершины M^* на сторону и есть искомое расстояние. Вспомним формулы для вычисления площади параллелограмма:

и .

Сравнивая их, будем иметь:

.

Это и есть искомая формула для расстояния от точки M^*(x^*,y^*,z^*), до прямой проходящей через точку M₀(x₀,y₀,z₀) в направлении вектора .