§9. Взаимное расположение двух прямых в пространтве

Пусть две прямые p₁ и p₂ в пространстве заданы своими каноническими уравнениями:

,

.

Параллельность, перпендикулярность и угол между прямыми вполне определяется их направляющими векторами и.

Условие параллельности:

.

Условие перпендикулярности:

.

Угол φ между прямыми определяется по формуле:

.

Две прямые в пространстве могут: 1) пересекаться; 2) быть параллельными; 3) скрещиваться. В первых двух случаях прямые лежат в одной плоскости. Наряду с направляющими векторами прямых и, рассмотрим вектор, где. Прямые лежат в одной плоскости тогда и только тогда, когда эти векторы компланарны, что, в свою очередь, равносильно равенству нулю их смешанного произведения. Выразив смешанное произведение через проекции векторов, получим условие принадлежности прямыхp₁ и p₂ одной плоскости:

.

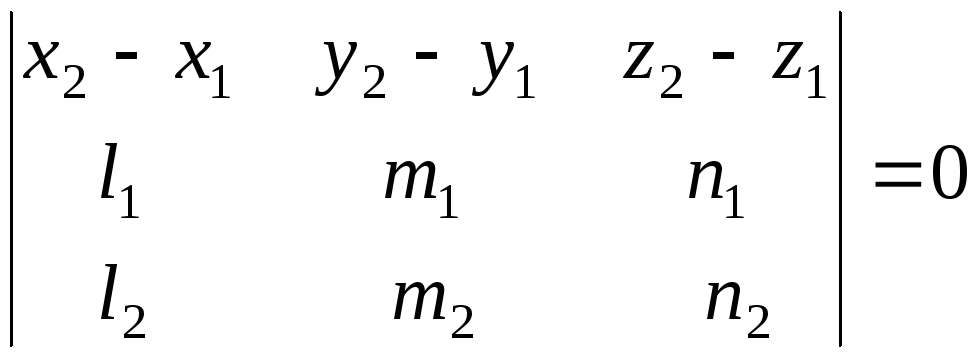§10. Взаимное расположение плоскости и прямой в пространстве

Пусть дана плоскость α: Ax+By+Cz+D=0 с нормальным вектором и прямаяс направляющим вектором, проходящая через точкуM₀(x₀,y₀,z₀).

α

φ

p

Условие параллельности прямой и плоскости:

.

Условие перпендикулярности прямой и плоскости:

.

Угол φ между прямой и плоскостью определяется по формуле:

Условия принадлежности прямой плоскости:

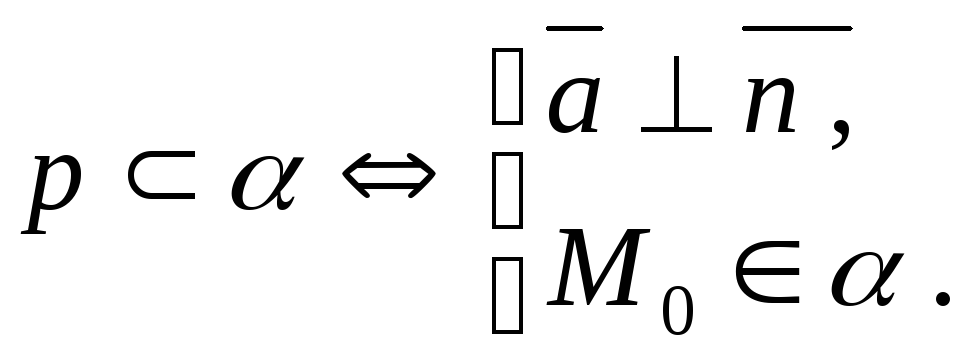
ЛЕКЦИЯ 9

Тема Линии второго порядка.

§1. Общее уравнение

Определение. Уравнение с двумя переменными вида

Ax²+By²+Cxy+Dx+Ey+F=0 (1)

называется уравнением второй степени, а линия, которую оно определяет – линией второго порядка (если только хотя бы один из старших коэффициентов A, B или C отличен от нуля).

При некоторых значениях коэффициентов уравнение (1) определяет так называемые вырожденные линии второго порядка: уравнение x²+y²=0 определяет одну точку O(0;0); уравнение x²+2y²+1=0 не определяет никакого геометрического образа; уравнения x²–y²=0 и x²–1=0 определяют пары прямых (пересекающихся и параллельных).

Если исключить из рассмотрения вырожденные линии, то собственно кривая второго порядка может быть одной из четырех типов: окружность, эллипс, гипербола, парабола.

Поворотом системы координат на некоторый угол (он определяется как решение уравнения (B–A)sin2α+Ccos2α=0), можно исключить из уравнения (1) член, содержащий произведение переменных. В дальнейшем будем считать, что такой поворот уже выполнен, т.е. в уравнении (1) коэффициент С=0. Тогда вид кривой определяется по коэффициентам A и B следующим образом:

1. A=B – уравнение (1) определяет окружность (или пустое множество, или единственную точку);

2. A∙B>0 (т.е. A и B одного знака) – уравнение определяет эллипс (или пустое множество, или точку);

3. A∙B<0 (т.е. A и B различного знака) – уравнение определяет гиперболу (или пару пересекающихся прямых);

4. A∙B=0 (в уравнении отсутствует квадрат одной из переменных) – уравнение определяет параболу (или пару параллельных прямых).

Путем выделения полных квадратов уравнение (1) можно привести к нормальной форме:

A(x–x₀)²+B(y–y₀)²+G=0 в случаях 1), 2), 3);

A(x–x₀)²+E(y–y₀)=0 или

B(y–y₀)²+D(x–x₀)=0 в случае 4).

Перенося начало системы координат в точку (x₀,y₀), получим канонические уравнения кривых второго порядка.