II Параметрическое задание линии

Определение 3. Если абсцисса и ордината произвольной точки линии заданы как функции некоторой вспомогательной переменной, а именно:

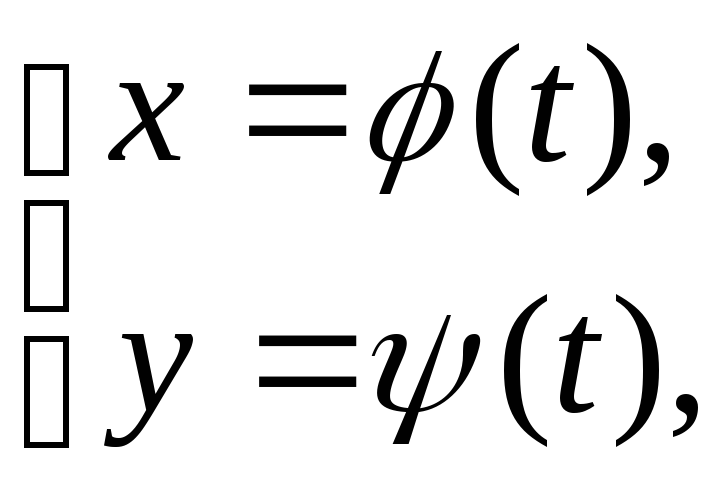(3)

то говорят, что линия задана параметрически. Уравнения (3) называют параметрическими, переменную t – параметром.

Параметрическое представление линии естественно возникает, если эту линию рассматривать как траекторию движения материальной точки, непрерывно движущейся по определенному закону.

В качестве примера установим параметрические уравнения окружности радиуса R с центром в начале координат. Пусть M(x,y) – текущая точка окружности, а t – угол между радиус-вектором этой точки и осью Ox, отсчитываемый в положительном направлении. Вспоминая определение синуса и косинуса произвольного угла, нетрудно получить

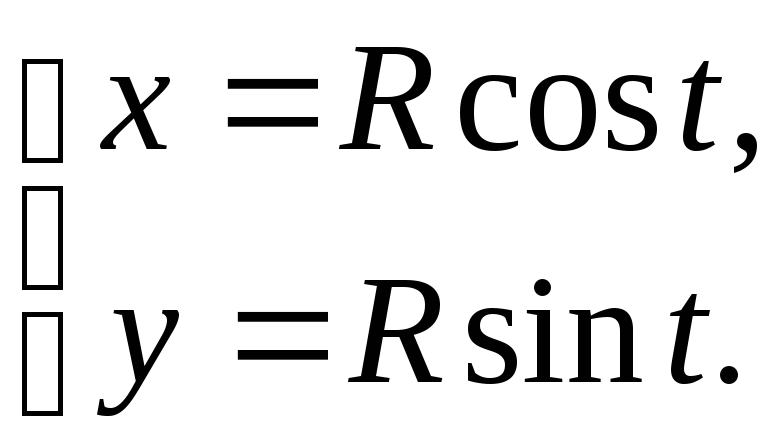(4)

Это и есть параметрические уравнения рассматриваемой окружности. Параметр может принимать любые значения, но для того, чтобы точка M(x,y) один раз обошла окружность, следует ограничить область измерения параметра, например, промежутком 0≤t<2π.

Замечание 3. Иногда удается из параметрических уравнений исключить параметр и прийти к уравнению вида F(x,y)=0. Например, если уравнения (4) возвести в квадрат и сложить, то получим известное уравнение рассматриваемой окружности: x²+y²=R².

Замечание 4. Часто линию L определяют не уравнением вида F(x,y)=0, а разрешенным относительно какой-либо переменной, например уравнением y=f(x). В таком случае говорят, что линия задана явно, линия является графиком функции. Заметим, что такой способ задания является частным случаем параметрического:

Иногда одно уравнение вида F(x,y)=0 распадается на несколько явных:

III о пересечении двух линий

В аналитической геометрии часто приходится решать задачу: даны две линии F₁(x,y)=0 и F₂(x,y)=0, требуется найти точки их пересечения. Как всегда в аналитической геометрии, говоря “найти точки”, мы подразумеваем: “вычислить их координаты”.

Само определение уравнения линии дает способ решения этой задачи: следует решить систему уравнений

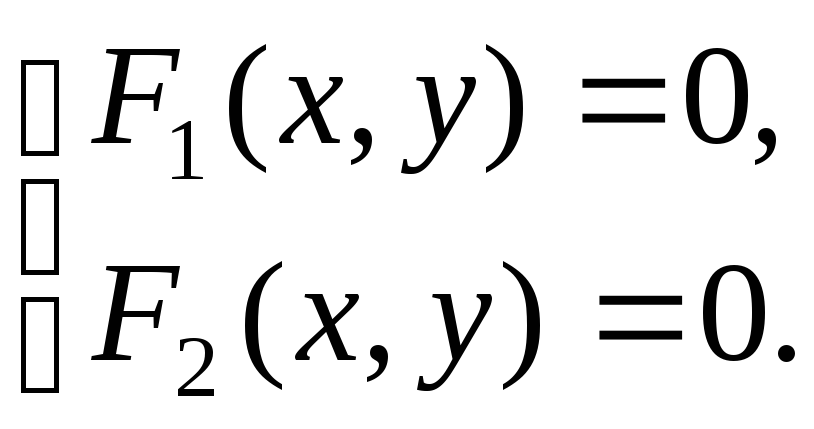
IV Уравнение линии в различных системах координат

Как уже отмечалось, вид уравнения линии L зависит не только от вида самой линии L, но и от выбора системы координат. Уравнение линии меняется как при переходе от одной ДПСК к другой, так и при переходе от декартовых координат к каким-нибудь другим.

Если есть уравнение линии в ДПСК, то получить уравнение в другой системе можно просто применив формулы перехода. Например:

x²+y²–2Rx=0 – в ДПСК,

, или после преобразования

–в ПСК.

Если же декартового уравнения нет, можно сразу получать уравнение в требуемой системе координат.

Пример. Отрезок длиной 2а движется так, что его концы находятся на положительных полуосях координат. Из начала координат на него опущен перпендикуляр. Составить уравнение линии, которую описывает основание этого перпендикуляра при движении отрезка.

y

Решение. Составим уравнение в ПСК.

В

П

φ

0

M

ρ

φ

A

x

устьM(ρ,φ) – текущая точка линии (основания перпендикуляра). Из элементарно-геометрических соображений имеем:

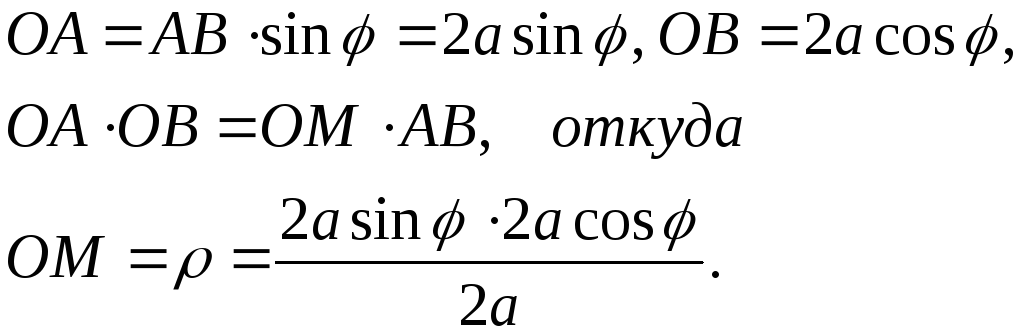
Окончательно, – полярное уравнение рассматриваемой линии.