IV Нормальное уравнение гиперболы

Гипербола, центр которой имеет координаты (x₀;y₀), а оси парал- лельны координатным осям, имеет уравнение

. (3)

Фокусы этой гиперболы лежат на прямой y=y₀.

Замечание 1. Уравнение вида

(4)

также определяет гиперболу. Ее фокусы и действительные вершины лежат на оси Oy. Гиперболы (1) и (4) в одной и той же системе координат и при одних и тех же значениях полуосей a и b называются сопряженными друг с другом.

Замечание 2. Гипербола с равными полуосями (a=b) называется равносторонней. Каноническое уравнение такой гиперболы пишут в виде

x²–y²=a². Ее асимптоты взаимно перпендикулярны.

Типовые задачи аналогичны задачам для эллипса.

§5. Парабола

I Каноническое уравнение параболы

Определение 1. Параболой называется линия, которая в некоторой ДПСК имеет уравнение

где p – некоторое положительное число.

Рассмотрим параболу (1). Т.к. замена y на (–y) не изменяет уравнения, это означает симметрию линии относительно оси Ox. В верхней полуплоскости уравнение (1) равносильно уравнению

. (3)

При x<0 корень не существует, следовательно, левее оси ординат ни одной точки параболы (1) нет. При x=0 получаем y=0: начало координат является самой “левой” точкой параболы (1) и с возрастанием x от 0 до

y возрастает аналогично. Методы математического анализа позволяют выяснить, что линия (3) выпукла вверх и в начале координат касается оси ординат. Асимптот у параболы нет.

II Определяющее свойство параболы

Для параболы (1) рассмотрим точку , которую назовем фокусом параболы, и прямую, которую назовем директрисой. И пусть точкаM(x,y)–произвольная точка параболы (1) т.е. x≥0, а y²=2px. Найдем расстояние от M до F и до d:

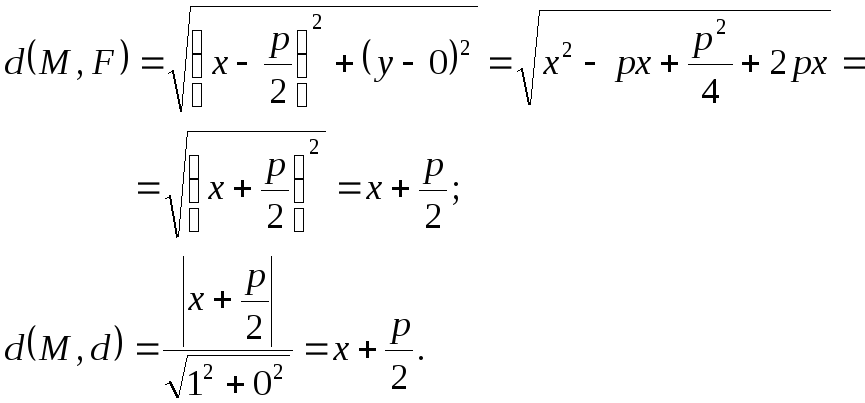
Итак, точки параболы равноудалены от фокуса и директрисы.

Это свойство (как и в случае эллипса и гиперболы) можно взять в качестве определения.

Определение 2. Парабола есть геометрическое место точек (плоскости) равноудаленных от данной точки (называемой фокусом) и данной прямой (называемой директрисой).

Исходя из этого определения, получим каноническое уравнение, для чего обозначим расстояние от фокуса F до директрисы d через p, а ДПСК выберем следующим образом: ось абсцисс проведем через фокус перпендикулярно к директрисе и будем считать ее направленной к фокусу от директрисы, а начало координат поместим посередине между F и d. В этой системе: и. Пусть теперьM(x,y) текущая точка параболы (определение 2). Заметим сразу, что M не может находиться левее оси ординат, ибо в этом случае d(M,F)>d(M,d). Найдем эти расстояния:

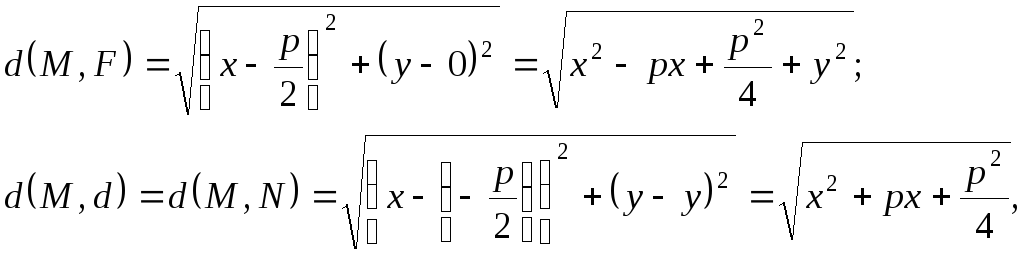
здесь – проекцияM на директрису. Приравняем (в соответствии с определением 2) полученные расстояния и для упрощения возведем обе части полученного равенства в квадрат (посторонние корни не появятся; почему?). После упрощения получим каноническое уравнение (1): y²=2px.

Замечание 1. Уравнение (2) получим, если ось Oy провести через F перпендикулярно к d и от d к F. Кроме уравнений (1) и (2) рассматривают еще два уравнения y²= –2px – ось Ox направлена от F к d, и x²= –2py – ось Oy направлена от F к d .